Квадрат – это геометрическая фигура с четырьмя равными сторонами и углами. В математике он используется как базовая единица измерения площади. Узнайте о свойствах квадрата и его применении в геометрии и алгебре в нашей статье.
Квадрат является одним из наиболее распространенных и важных геометрических фигур в математике. Это двумерная фигура, которая имеет четыре равные стороны и углы в 90 градусов друг с другом. В математике квадрат описывается через его сторону – длина, которая обозначается буквой “а” или словом “сторона”.
Квадрат является простым примером единицей измерения длины – квадратным метром (m²). Кроме того, квадрат имеет несколько важных особенностей, которые используются в различных математических приложениях, включая геометрию, экономику и физику.
Существует множество интересных и полезных свойств квадрата, включая его площадь, периметр, диагональ и радиус вписанной окружности. Понимание этих свойств квадрата может быть полезным для решения различных задач и проблем в математике и других областях знания.
Квадрат в математике: определение и особенности
Квадрат – это геометрическая фигура, которая имеет четыре равные стороны и четыре прямых угла. В математике квадрат – это один из базовых объектов, который важен в различных областях, включая геометрию, алгебру и теорию чисел.
Основная особенность квадрата – равенство всех его сторон и прямых углов. Кроме того, каждый угол квадрата равен 90 градусам, и диагонали квадрата пересекаются под прямым углом. Для расчета площади квадрата нужно возвести длину любой из его сторон в квадрат.
Квадраты используются в различных математических задачах. Например, в геометрии квадрат является идеальной формой для создания сеток или для измерения площадей. В алгебре квадрат является одним из базовых элементов, используемых для построения сложных функций и формул.
Квадрат имеет множество интересных свойств, которые могут быть использованы для решения различных математических задач. Если, например, знать площадь квадрата, то можно легко вычислить его стороны. Квадрат также может использоваться для решения проблем, связанных с расположением объектов.
Понятие квадрата:
Квадрат – это геометрическая форма, которая имеет четыре равных стороны и четыре прямых угла. Он также является ромбом, который соединен с прямоугольником, поэтому он обладает свойствами как ромба, так и прямоугольника.
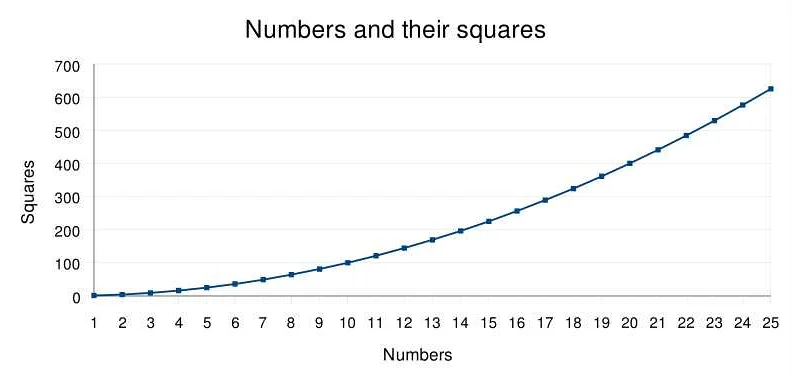
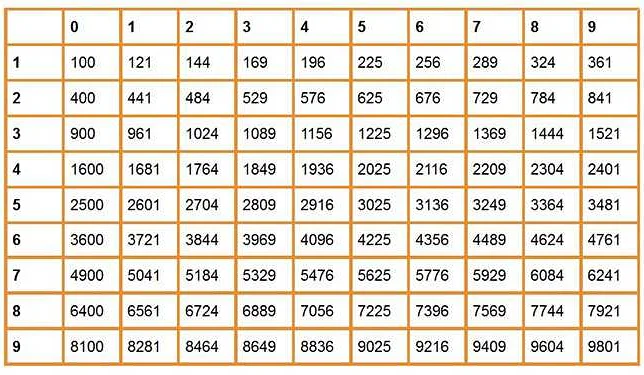
В математике, квадратом называется число, которое получается умножением числа на само себя. Например, 5 в квадрате равно 25, так как 5*5=25. Каждое целое число можно возвести в квадрат, и результат всегда будет положительным числом.
Кроме того, квадрат является простой фигурой, что делает его легко узнаваемым и используемым в геометрических задачах. Его свойства и характеристики изучаются в начальной и средней школе, а также в курсах алгебры и геометрии в более продвинутых уровнях обучения.
Среди свойств квадрата можно выделить:
- Все углы квадрата равны 90 градусам;
- Диагонали квадрата равны друг другу и делят его на четыре равных треугольника;
- Периметр квадрата равен сумме длин его сторон;
- Площадь квадрата равна квадрату длины его стороны.
Квадрат является не только основной в геометрии, но и в математических вычислениях. Он широко используется в геометрических задачах, а также в алгебре при решении уравнений и задач, связанных с числами и их свойствами.
Формула для вычисления периметра квадрата:
Квадрат – это четырехугольник со сторонами, равными друг другу. Для вычисления периметра квадрата необходимо сложить длины его сторон:
P = 4a, где P – периметр квадрата, а – длина стороны.
Таким образом, мы получаем, что периметр квадрата равен четырем умножить на длину его стороны.
Например, если длина стороны квадрата равна 5 см, то его периметр будет:
- P = 4 * 5 = 20 см.
Знание формулы для вычисления периметра квадрата может пригодиться в решении различных задач по математике и в повседневной жизни.
Формула для вычисления площади квадрата:
Квадрат – это геометрическая фигура, обладающая 4 равными сторонами и 4 углами равными по 90 градусов. Площадь квадрата можно вычислить, умножив значение длины его стороны на саму себя.
Формула для вычисления площади квадрата:
S = a2, где S – площадь квадрата, а – длина его стороны.
Например, если длина стороны квадрата равна 5 см, то его площадь будет равна:
- S = 52 = 25 квадратных сантиметров.
А если длина стороны квадрата равна 10 см, то его площадь будет равна:
- S = 102 = 100 квадратных сантиметров.
Таким образом, формула для вычисления площади квадрата является достаточно простой и понятной, что делает ее удобной в использовании при решении различных задач.
Свойства квадрата:
1. Все стороны квадрата равны между собой: Квадрат имеет четыре стороны, каждая из которых равна друг другу. Это свойство позволяет нам вычислять длину сторон, зная длину одной из сторон квадрата.
2. Углы квадрата прямые: Каждый угол квадрата равен 90 градусам, что делает его прямоугольным. Это свойство позволяет нам использовать теорему Пифагора для вычисления длины диагонали квадрата.
3. Диагонали квадрата равны между собой: Диагональ, проходящая через центр квадрата, делит его на два треугольника, которые являются равнобедренными. Это означает, что длина каждой из диагоналей квадрата равна друг другу.
4. Площадь квадрата равна квадрату длины его стороны: Площадь квадрата выражается как произведение длины его стороны самой на себя (S = a * a или S = a^2).
5. Периметр квадрата равен четырем длинам его сторон: Периметр квадрата это сумма длин всех его сторон (P = 4a). Это свойство позволяет нам вычислить периметр квадрата, зная длину одной из его сторон.
Как измерить диагональ квадрата:
Диагональ квадрата – это отрезок, соединяющий противоположные вершины фигуры. Вычислить длину диагонали поможет теорема Пифагора:
Теорема Пифагора: В прямоугольном треугольнике квадрат на гипотенузе равен сумме квадратов катетов.
Таким образом, чтобы найти длину диагонали квадрата, необходимо умножить длину одной из сторон на корень из двух:
Длина диагонали квадрата = длина стороны × √2
Например, если сторона квадрата равна 5 см, то его диагональ будет равна:
5 × √2 ≈ 7,07 см
Итак, теперь мы знаем, как измерить длину диагонали квадрата с помощью формулы и теоремы Пифагора.
Квадрат в геометрии:
Квадрат – это четырехугольник, у которого все стороны равны и все углы прямые. Он относится к классу прямоугольников, но отличается тем, что все его стороны равны. В геометрии квадрат является одной из основных фигур.
Квадрат широко используется в различных областях, включая строительство, дизайн, графику и другие. Он является идеальной фигурой для применения в расчетах площади или объема объектов, а также для создания графических изображений.
Квадрат имеет множество интересных свойств и характеристик, которые часто используются в математике для решения различных задач. Например, его диагонали имеют одинаковую длину и пересекаются под прямым углом в центре фигуры.
Важно понимать различия между квадратом и прямоугольником, поскольку это может существенно влиять на результат математических расчетов. Если необходимо расчитать площадь квадрата, то достаточно возвести длину одной стороны в квадрат. В случае же с прямоугольником нужно умножить длину на ширину.
- Вывод: Квадрат является одной из базовых геометрических фигур с четырьмя равными сторонами и прямыми углами.
- Важно запомнить: Квадрат является прямоугольником, но прямоугольник не является квадратом.
Применение квадрата в математике:
Квадраты используются в различных областях математики, в том числе в алгебре и геометрии. Одно из наиболее распространенных применений квадрата – вычисление площади квадрата. Для этого длина каждой стороны квадрата умножается на себя.
В алгебре квадрат используется для возведения числа в квадрат. Это означает, что число умножается само на себя. Также квадрат используется при решении квадратных уравнений, где ищется значение неизвестной переменной, которое можно записать в квадратном виде.
В геометрии квадрат используется для нахождения диагонали квадрата. Квадрат также может использоваться как базовый элемент для создания других геометрических фигур, таких как прямоугольник или ромб.
Одно из наиболее захватывающих применений квадратов – матрицы, которые используются в линейной алгебре и компьютерной графике для хранения и обработки данных. Матрица – это таблица чисел, которые могут быть квадратными или неквадратными.
В целом, квадраты часто используются в математике как базовый элемент для нахождения площади, возведения чисел во вторую степень, нахождения корней из уравнений, и многое другое.
Квадрат и другие геометрические фигуры:

Квадрат – это геометрическая фигура, которая имеет четыре равных стороны и четыре прямых угла. Квадрат используется в математике для описания площади поверхности и объема многих объектов, включая коробки, кубы и другие.
Треугольник – это геометрическая фигура, которая имеет три стороны и три угла. Треугольник используется в математике для описания геометрических свойств многих объектов, включая острова, крыши и фасады зданий.
Круг – это геометрическая фигура, которая имеет радиус и центр. Круг используется в математике для описания площади поверхности и объема многих объектов, включая колеса, ступени и другие.
Прямоугольник – это геометрическая фигура, которая имеет две пары равных противоположных сторон и четыре прямых угла. Прямоугольник используется в математике для описания площади поверхности и объема многих объектов, включая окна, двери и столы.
Примеры объектов, описываемых квадратом и другими геометрическими фигурами
| Квадрат | Треугольник | Круг | Прямоугольник |
| Книги | Острова | Колеса | Столы |
| Коробки | Фасады зданий | Ступени | Окна |
| Кубы | Крыши | Тарелки | Двери |
Вопрос-ответ:
Что такое квадрат в математике?
Квадрат в математике – это фигура, у которой все стороны равны и углы прямые. Также квадрат можно определить как параллелограмм с равными сторонами и прямыми углами.
Интересные факты о квадрате:
1. Квадрат – это фигура со всеми равными сторонами и углами. Это означает, что все стороны квадрата имеют одинаковую длину, а углы между ними равны 90 градусов. Благодаря этому свойству квадрат можно легко различить от других геометрических фигур.
2. Четыре стороны квадрата всегда равны между собой. Если сторона квадрата равна “а”, то периметр квадрата можно выразить по формуле P = 4a. Также сумма всех углов квадрата равна 360 градусов.
3. Квадрат используется во многих аспектах нашей жизни. Например, квадрат является основой для укладки плитки на полу или стене. Также квадрат используется в геометрии при расчёте площади фигур, а в математике – для построения графиков. В физике квадрат используется для измерения различных характеристик, например, для вычисления площади поверхности тела.
4. Символ квадрата используется в математике для обозначения возведения числа во вторую степень. Например, 4² означает число 4, возведённое в квадрат, то есть 4 умножить на 4 и равняется 16. Это свойство квадрата широко применяется в физике и инженерных расчётах.
5. На Интернете есть забавное математическое задание под названием “Квадраты”. В этом задании игрокам нужно провести линию через все квадраты на игровом поле, не поднимая её и не опуская. Задание кажется простым, но чем больше квадратов на поле, тем сложнее его решить.






