Игрек в математике – это буква алфавита, которая используется для обозначения второй координаты на координатной плоскости. Она обычно используется вместе с буквой ‘х’, которая обозначает первую координату. Узнайте, как использовать игрек в математических расчетах и задачах.
В математике одним из важных аспектов являются координатные плоскости, на которых выполняются различные математические операции. В этой системе координат используются две оси: горизонтальная, которая называется осью абсцисс, и вертикальная, которая называется осью ординат. Значения на оси абсцисс обозначаются буквой “x”, а на оси ординат — буквой “y”.
Кроме того, в математике часто используется буква “z” для обозначения координаты в трехмерном пространстве. Но наряду с этими буквами в математических выражениях часто встречается буква “i” и “j”, которые используются для обозначения единичных векторов. Но сейчас мы сосредоточимся на букве “y”.
Буква “y” обозначается как игрек, и является общепринятым обозначением для переменной на оси ординат в математике. Появление игрека в математических формулах обязательно в тех случаях, когда требуется обозначить координату, которая находится на вертикальной оси.
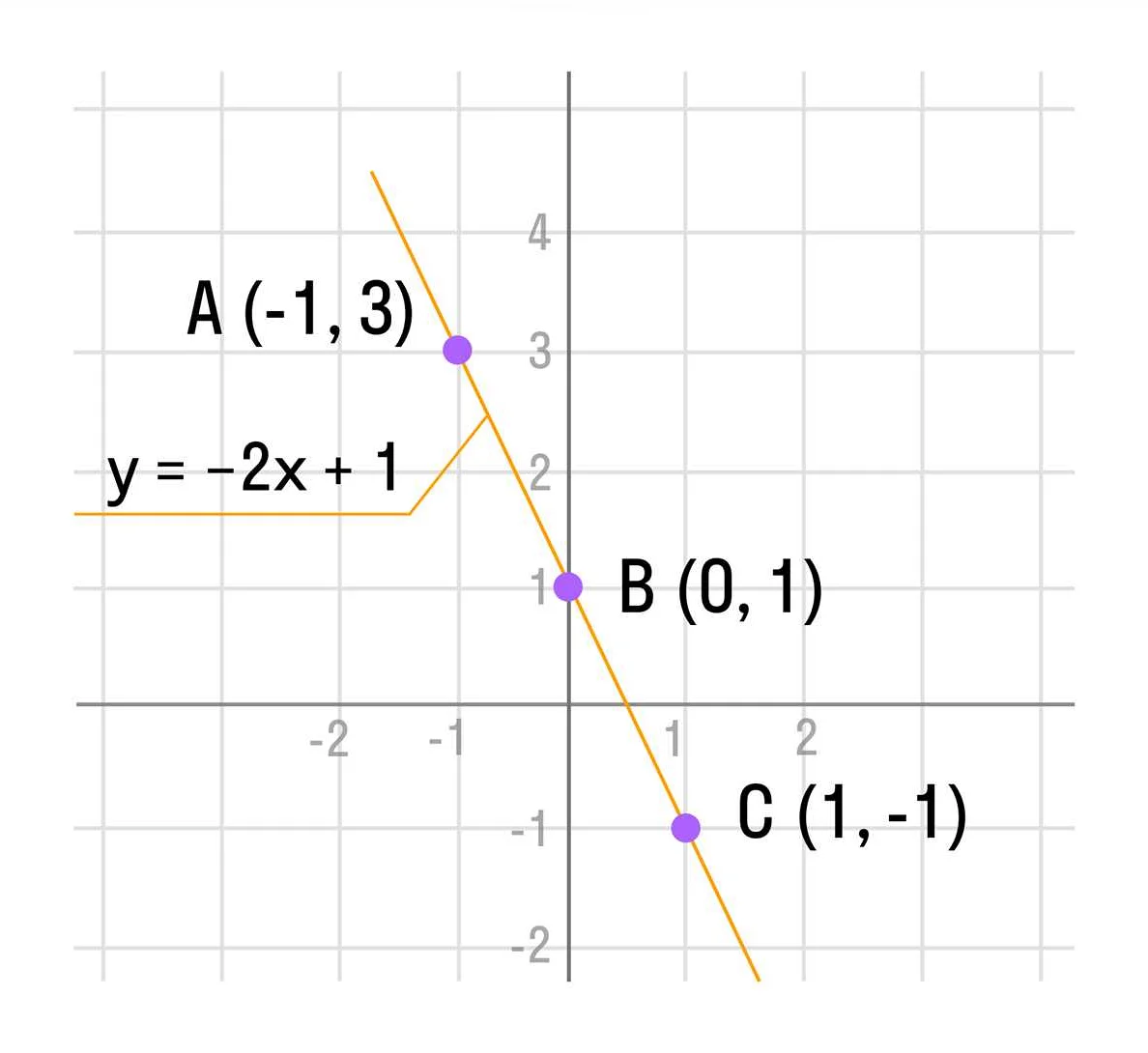
Пожалуй, наиболее известным примером использования игрека в математике является уравнение прямой, которое имеет вид y = kx + b, где “y” обозначает координату на вертикальной оси, “k” — угловой коэффициент и “b” — точку пересечения с вертикальной осью, которые определяют график прямой линии на координатной плоскости.
Что такое игрек в математике

В математике “игрек” (y) обозначает переменную, которая используется для обозначения зависимой переменной в уравнении функции. Обычно она располагается на оси ординат, а ее значение изменяется в зависимости от значения переменной на оси абсцисс (x).
В уравнении прямой, например, y = kx + b, игрек (y) обозначает значение координаты точки на оси ординат, в которой прямая пересекает или пересекала ось y, а абсцисса (x) – значение координаты точки на оси абсцисс, в которой она пересекает ось x.
Игрек (y) используется не только в уравнениях функций, но и в других областях математики, таких как геометрия, алгебра и анализ. Например, в треугольнике координаты вершин обычно обозначаются буквами X и Y для осей абсцисс и ординат соответственно, а длины сторон и углы – другими переменными, в том числе и игреком (y).
Таким образом, игрек (y) является одним из ключевых элементов математической нотации и широко используется в решении различных математических задач и проблем.
Видео по теме:
Зачем нужен игрек в математике

Игрек – это одна из переменных, которая используется в математике для обозначения второй координаты на координатной плоскости. Игрек не менее значим, чем другая переменная, которая обозначает первую координату – абсциссу.
Основное назначение игрек заключается в работе с графиками функций. Именно благодаря игреку мы можем построить график функции на плоскости. К примеру, если на плоскости имеется точка (3, 4), то 3 является абсциссой этой точки, а 4 – игреком. Таким образом, игрек помогает описывать положение объектов в пространстве.
Кроме того, игрек используется для решения математических задач. Например, для нахождения расстояния между двумя точками на плоскости необходимо использовать формулу длины отрезка, в которой присутствует игрек. Использование игрека сильно упрощает работу с геометрическими фигурами, что позволяет решать задачи более быстро и точно.
Таким образом, игрек имеет большое значение в математике и используется практически при любом расчете на плоскости. Без игрека невозможно получить корректные результаты и описания геометрических объектов.
Пример использования игрека в геометрии
В геометрии игрек (y) часто используется для обозначения оси ординат на координатной плоскости. Также, игрек может использоваться для обозначения значения координаты точки на этой оси.
Рассмотрим пример использования игрека в геометрии на простом графике функции:
- Функция: y = x^2
- Значения x: -3, -2, -1, 0, 1, 2, 3

На графике значение функции (y) может быть найдено для любого значения x. Например, когда x = 2, значение функции будет равно y = 4.
Таким образом, игрек в геометрии удобен для обозначения координат точек на оси ординат и использования их в математических вычислениях.
Вопрос-ответ:
Пример использования игрека в алгебре
Игрек является неотъемлемой частью алгебры и широко используется в различных задачах и уравнениях. Одним из примеров использования игрека является решение уравнения y = x + 3.
Для решения данного уравнения необходимо заменить x на игрек (y – 3), тогда получим уравнение:
y – 3 = x + 3
Далее, нужно раскрыть скобки и привести подобные члены:
y – 3 = y + 3
-3 = 3
Как видим, данное уравнение нерешаемо и не имеет корней. Однако, мы продемонстрировали, как использовать игрек в алгебре для решения уравнений.
Как работать с игреком
Шаг 1: Используйте игрек для представления функции, которая зависит от переменной. Обозначение игрека – y. Например, y = 2x + 1.
Шаг 2: Используйте игрек для создания графика функции. Разметьте оси x и y и отметьте значения функции на графике. График функции y = 2x + 1 выглядит как прямая с углом наклона 2 и смещением пересечения со осью y в 1.
Шаг 3: Используйте игрек для нахождения значений функции в заданной точке. Если нужно определить значение функции y = 2x + 1 в точке x=3, то нужно подставить 3 вместо переменной x: y = 2(3) + 1 = 7.
Шаг 4: Используйте игрек для решения уравнений и неравенств. Если нужно решить уравнение 2x + 1 = 5, то нужно перенести свободный член на другую сторону: 2x = 4, x = 2. Если нужно решить неравенство 2x + 1 < 5, то нужно вычесть 1 из обеих сторон: 2x < 4, x < 2.
Шаг 5: Используйте игрек для анализа поведения функции. Изменение значения переменной x может привести к изменению значения функции y. Коэффициенты уравнения функции обозначают угол наклона графика и смещение пересечения с осью y. При наличии отрицательного коэффициента происходит изменение направления графика функции.
Какие ошибки допускают при работе с игреком

Работа с игреком в математике может быть достаточно сложной и требовать от исполнителя высокой концентрации. При этом могут возникнуть ошибки, которые мешают правильному решению задачи.
1. Неправильная позиция игрека. Одной из распространенных ошибок при работе с игреком является неправильное размещение его на графике. Это может привести к неправильному определению координат точки, что повлияет на правильность решения задачи.
2. Не учет знака игрека. В математике игрек не всегда положителен, может быть отрицательным. Неучет знака может привести к ошибкам расчетов и неверному ответу.
3. Неправильная интерпретация графика. Работа с игреком тесно связана с анализом графика. Неправильная интерпретация графика может привести к неверному определению координат точки игрека, что в свою очередь может повлиять на правильность решения задачи.
4. Ошибки при подстановке значений. Иногда ошибки при работе с игреком связаны с неправильной подстановкой значений в формулу или пропуском этапов решения задачи. Внимательность и аккуратность помогут избежать подобных ошибок.
Разбор сложных примеров с использованием игрека
Игрек (y) является важным элементом математических формул и уравнений. С помощью этой переменной можно описать функции, графики, а также проводить анализ данных. Для того чтобы правильно использовать игрек, необходимо знать его определение и основные принципы работы.
Пример использования игрека может быть следующим:
xy
| 1 | 3 |
| 2 | 5 |
| 3 | 7 |
| 4 | 9 |
В данном случае, игрек отображает значение функции (y) при конкретном значении аргумента (x). С помощью этой таблицы можно построить график функции, например, как прямую линию, которая проходит через все эти точки.
Еще один пример использования игрека может быть в математических уравнениях, например, y = 2x + 3. Здесь игрек означает значение функции (y), которое получится при данном значении аргумента (x) и коэффициентам уравнения.
Таким образом, игрек является неотъемлемым элементом математических вычислений и важен для работы с функциями, графиками и уравнениями. Знание его определения и принципов работы поможет правильно проводить анализ данных и решать сложные математические задачи.
Какие еще математические символы можно использовать вместе с игреком
Игрек в математике – это буква Y, которую часто используют в уравнениях и графиках. Но помимо игрека, существуют и другие математические символы, которые можно использовать вместе с ним, например:
- X – буква X, которую также используют вместе с игреком в уравнениях и графиках.
- alpha, beta, gamma – символы греческого алфавита, которые используются в математике для обозначения углов, ускорения и других величин.
- pi – символ, который представляет собой отношение длины окружности к её диаметру. Используется в геометрии и математическом анализе.
- sigma – символ суммирования, который используется для обозначения суммы ряда. Используется в математическом анализе и статистике.
Некоторые другие символы, которые можно использовать вместе с игреком, – это дельта, эпсилон, lambda, фи, тета и омега. Как правило, эти символы используются для обозначения различных математических функций и величин.
В целом, математическая нотация может быть довольно сложной, но использование правильных символов может помочь усовершенствовать вашу работу и сделать её более точной.
Как использовать игрек при программировании
Игрек ( y ) является переменной в математике и может быть использован в программировании для хранения значений. Разные языки программирования могут использовать разные обозначения переменных, но часто игрек используется как обозначение для оси у в графике.
При программировании использование игрека позволяет получить значительные преимущества, например, при создании графиков и математических функций. В Python, например, библиотека Matplotlib используется для рисования графиков, где игрек обозначает значение на оси y.
Кроме того, при работе с базами данных в программировании игрек может использоваться для хранения и извлечения значений, связанных с осью y. Это также может быть полезно при создании отчетов и статистических данных.
Как и в математике, игрек может быть использован в программировании как независимая переменная, когда ему присваиваются значения для оценки различных параметров функции. Например, в программировании составления расписаний, игрек может быть использован для представления времени и распределения задач по времени.
В целом, использование игрека при программировании позволяет работать с математическими функциями и данными более эффективно и удобно. Однако, важно помнить, что игрек может использоваться только в тех языках программирования, где переменные могут быть обозначены буквами и не являются зарезервированными словами.
Пример использования игрека в программировании
Игрек, обозначающий вертикальную координату на плоскости, широко используется в программировании. Особенно часто он встречается при работе с графиками и кривыми.
Например, при прорисовке графика функции y = f(x) в программе на языке Python, мы используем игрек для задания вертикальных координат точек на графике.
Вот пример кода для построения графика функции y = x^2 в Python:
import matplotlib.pyplot as plt
x = [i/10 for i in range(-100,101)]
y = [x[i]**2 for i in range(len(x))]
plt.plot(x, y)
plt.show()
В этом примере мы создаем список x, который содержит значения аргумента функции в диапазоне [-10,10], а затем создаем список y, содержащий соответствующие значения функции при каждом значении x. Затем мы используем функцию plot из библиотеки matplotlib.pyplot для построения графика функции на координатной плоскости. Функция plot принимает два аргумента – список значений по оси x и список значений по оси y.
Таким образом, использование игрека в программировании позволяет нам легко работать с вертикальными координатами на координатной плоскости и построить графики и кривые в программных приложениях.






