Проценты – одна из основных тем математики в 5 классе. Статья расскажет, что такое процент и как его использовать в задачах на практике.
Раздел математики, который называется проценты, необходим для каждого ученика в любом классе. Ведь проценты встречаются в повседневной жизни, они распространены в магазинах, банках, на рынке труда и в других областях. Суть процентов заключается в том, что они выражают одну величину относительно другой измеренной такой же величины.
В этой статье мы рассмотрим базовые понятия в процентах, а также основные формулы, которые помогут вам понять эту тему. Мы также рассмотрим применение процентов в простых и более сложных задачах. Надеемся, что после прочтения этой статьи вы будете более уверенно использовать проценты в повседневной жизни и в школьных задачах.
Начнем со следующего понятия: процент это доля в сотых долях. Другими словами, процент – это выражение, которое означает, сколько одной величины соответствует величина другой в стах долях. Проценты записываются как дробь с числителем и знаменателем, где числитель – это число процентов, а знаменатель соответствует 100.
Проценты в математике для 5 класса:
Проценты – это дроби с знаменателем 100. В математике для 5 класса проценты используются для выражения отношения одного числа к другому в процентном выражении. Например, если 20 из 100 учеников в классе имеют отличные оценки, то это значит, что процент таких учеников равен 20%.
Для вычисления процентов в математике для 5 класса используются основные формулы, такие как:
- Процент от числа: процент * число / 100
- Число, соответствующее проценту: процент * 100 / процентное отношение
- Процентное отношение: число / число, соответствующее проценту * 100
Проценты используются в различных областях жизни, включая финансы, экономику, науку и технику. Умение работать с процентами является важной частью математической грамотности и помогает в повседневной жизни при покупке товаров со скидкой или вычислении процентной ставки по кредиту.
Видео по теме:
Понятие процентов
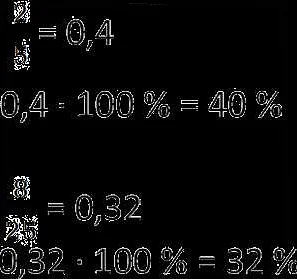
Проценты – это один из важных элементов математики, которые мы используем в повседневной жизни. Проценты показывают, какая часть из 100 возможных используется или отмечается в чем-то.
Например, если в магазине проводится скидка в 20%, то это означает, что цена товара уменьшится на 20% от начальной. То есть, если начальная цена товара была 1000 рублей, то после скидки он будет стоить 800 рублей.
Проценты используются не только при скидках, но и при расчете процентной ставки по банковскому вкладу или кредиту, при рассчете налогов и так далее.
Понимание процентов является важным навыком для нашей финансовой грамотности и может помочь нам не только лучше понимать наши расходы и доходы, но и рассчитывать эффективную прибыль на свои вложения.
Как вычислять проценты?
Процентом называют десятую часть числа. Например, 30% – это 30 из 100.
Для того, чтобы вычислить процент от числа, нужно умножить число на процент и разделить на 100. Формула выглядит следующим образом:
| Число x % = (x * %)/100 |
Например, если нужно вычислить 20% от 500, то нужно выполнить следующие действия:
- Умножаем 500 на 20: 500 * 20 = 10000
- Делим на 100: 10000 / 100 = 100
Таким образом, 20% от 500 равно 100.
Увеличение или уменьшение числа на процент. Если нужно увеличить число на процент, то нужно к числу прибавить процент от него. Если нужно уменьшить число на процент, то нужно из числа вычесть процент от него. Формулы для таких операций выглядят следующим образом:
| Увеличение числа на % = число + (число * %)/100 |
| Уменьшение числа на % = число – (число * %)/100 |
Например, если нужно увеличить 500 на 30%, то нужно выполнить следующие действия:
- Умножаем 500 на 30: 500 * 30 = 15000
- Делим на 100: 15000 / 100 = 150
- Прибавляем к числу: 500 + 150 = 650
Таким образом, 30% увеличение числа 500 равно 650.
Вопрос-ответ:
Что такое проценты и зачем их изучать в 5 классе?
Проценты – это способ представления доли чего-либо в виде сотых долей. Через проценты мы можем сравнивать различные величины и делать выводы о том, какие из них больше или меньше. Изучение процентов помогает учащимся развивать математическое мышление и повышать культуру мышления.
Как вычислить процент от числа?
Чтобы вычислить процент от числа, нужно умножить это число на процент и разделить на 100. Например, чтобы найти 20% от 100, нужно выполнить следующую операцию: 100 * 20 / 100 = 20. Таким образом, 20% от 100 равно 20.
Как найти число при известном проценте и доле?
Чтобы найти число при известном проценте и доле, нужно разделить долю на процент и умножить на 100. Например, если 20% от числа X равно 40, то X можно найти следующим образом: 40 / 20 * 100 = 200. Таким образом, число X равно 200.
Как найти процент при известном числе и доле?
Чтобы найти процент при известном числе и доле, нужно разделить долю на число и умножить на 100. Например, если 20 является 25% от числа X, то процент можно найти следующим образом: 20 / X * 100 = 25. Таким образом, процент равен 25%.
Как найти число при известном проценте и процентной ставке?
Чтобы найти число при известном проценте и процентной ставке, нужно умножить процент на процентную ставку и разделить на 100. Например, если 10% от числа X равно 150, а процентная ставка составляет 5%, то X можно найти следующим образом: 150 * 100 / 5 = 3000. Таким образом, число X равно 3000.
Как найти процент при известном числе и процентной ставке?
Чтобы найти процент при известном числе и процентной ставке, нужно умножить число на процентную ставку и разделить на 100. Например, если 20 является 10% от числа X, а процентная ставка составляет 2%, то процент можно найти следующим образом: 20 * 100 / 2 = 1000. Таким образом, процент равен 1000%.
Какие задачи можно решить, используя знания о процентах?
Знания о процентах могут использоваться при решении многих задач в различных областях. Например, проценты используются при расчетах налогов и скидок в магазинах, при расчете процентных ставок по кредитам, при определении роста и убыли на рынках ценных бумаг и т.д. Кроме того, знания о процентах могут быть полезны при решении задач по математике и экономике.
Основные формулы процентов

Процент – это долю от 100. Когда мы говорим о процентах, мы обычно имеем в виду какую-то долю или часть чего-либо. Например, 20% означает 20 из 100.
Давайте рассмотрим основные формулы процентов:
- Процент от суммы – это формула, которая используется для вычисления процента от суммы. Формула выглядит так: процент = (сумма х процент) / 100.
- Сумма с процентом – эта формула используется для вычисления суммы после добавления процента. Формула выглядит так: сумма с процентом = сумма + (сумма х процент) / 100.
- Изменение процентов – эту формулу используют, когда нужно вычислить, на сколько процентов изменилось значение. Формула выглядит так: процент изменения = (новое значение – старое значение) / старое значение х 100.
Знание этих формул позволит быстро и точно вычислять проценты и решать задачи на эту тему.
Применение процентов в жизни и бизнесе

Проценты – это одна из важнейших математических концепций, которые используются повсеместно в жизни и бизнесе для вычисления процентного роста или уменьшения определенных значений.
В жизни, например, знание процентов может помочь при расчетах скидок на покупки, расчете процента на кредитную карту, определении процента сбережений на банковском вкладе, а также при сравнении процентной ставки по ипотеке.
В бизнесе проценты используются для расчета налогов и налоговых вычетов, прогнозирования ставок обмена валюты для международных операций, расчета производственной и финансовой эффективности, а также при определении размера дивидендов и долей владения акциями.
Знание процентов и умение использовать простые математические формулы, связанные с процентами, является необходимым навыком для осознанного принятия решений в бизнесе и повседневной жизни, что может помочь в экономии времени и денег, а также в уменьшении риска допущения ошибок.
Кроме того, понимание процентов обеспечивает мощный инструмент, который применяется в анализе и оценке инвестиционных возможностей, а также в разработке стратегий долгосрочного финансового планирования.
Примеры задач на проценты

Пример 1: Шоколадка стоит 30 рублей. На следующей неделе цена на неё повысится на 10%. Сколько будет стоить шоколадка?
Решение:
- Найдем, насколько процентов увеличилась цена: 30 * 10% = 3 рубля.
- Теперь добавим этот процент к изначальной цене шоколадки: 30 + 3 = 33 рубля.
Ответ: Шоколадка будет стоить 33 рубля.
Пример 2: В ресторане группа из 6 друзей решила оплатить счет поровну. Но один из них опоздал и не успел дать свою часть. Теперь каждый должен заплатить на 15% больше, чтобы покрыть его долг. Сколько процентов от общего счета составит его долг?
Решение:
- Найдем общую сумму, которую должны заплатить 6 человек: 100% / 6 = 16,67%.
- Увеличим этот процент на 15% из-за долга друга: 16,67% * 15% = 2,50%.
Ответ: Долг друга составляет 2,50% от общей суммы.
Пример 3: Ипотечный кредит на сумму 500 000 рублей выдан на 20 лет под 11% годовых. Какую сумму придется выплатить в банк за весь период кредита?
Решение:
- Найдем, сколько процентов будет начислено на кредит за 20 лет: 11% * 20 = 220%.
- Теперь найдем, сколько это будет денег по текущей сумме кредита: 500 000 * 220% = 1 100 000 рублей.
- Добавим к этой сумме исходную сумму кредита: 1 100 000 + 500 000 = 1 600 000 рублей.
Ответ: Всего придется выплатить 1 600 000 рублей за весь период кредита.
Как решать задачи на проценты в математике для 5 класса?
Решение задач на проценты в математике в 5 классе основано на знании формулы процента, которая выглядит следующим образом:
Процент = (часть / целое) * 100%
Чтобы решить задачу на проценты, нужно понимать, какую часть от целого составляет процент. Например, если нужно посчитать 20% от 500, то сначала нужно найти, какую часть от 500 составляет 20%. Для этого применяем формулу процента:
20% = (часть / 500) * 100%
Далее находим неизвестную часть, умножив обе стороны уравнения на 500:
часть = (20% * 500) / 100% = 100
Ответ: 20% от 500 равно 100.
Однако решение задач на проценты может иметь различные вариации. Например, в некоторых задачах известна не процентная ставка, а процентная разница, то есть на сколько процентов меняется цена или количество. В этом случае нужно использовать формулу:
Часть (разница) = (цена / (100% +/- процентная разница)) * процентная разница
Таким образом, для решения задач на проценты в математике для 5 класса важно понимать не только формулу процента, но и уметь применять ее в различных ситуациях.
Методы решения задач на проценты: процент напрямую и косвенный процент
Задачи на проценты — один из самых важных разделов математики, который помогает понимать, как изменяются величины в процессе времени и как рассчитывать стоимость товара. Существует два метода решения задач на проценты: процент напрямую и косвенный процент.
Процент напрямую:
- Этот метод используется, когда известна исходная величина и на сколько процентов она увеличилась или уменьшилась.
- Формула проста: Изначальная величина ± Изначальная величина × процентный показатель / 100.
- Пример: Если цена на товар выросла на 20%, то новая цена может быть рассчитана как Изначальная цена + Изначальная цена × 20 / 100.
Косвенный процент:
- К этому методу прибегают, когда нужно узнать, на какой процент нужно увеличить или уменьшить значения нескольких величин, чтобы получить определенный результат.
- Принимая за основу одну конечную величину и несколько начальных, можно использовать следующую формулу: (Конечная величина / Произведение начальных величин) – 1 × 100%.
- Пример: Если цена на шоколадки выросла на 10%, цена на молоко выросла на 5%, а цена на печенье на 15%, определим, на сколько нужно снизить стоимость всех трех товаров, чтобы их суммарная стоимость уменьшилась на 10%. Для этого используем формулу: (1 – 0.9 / (1 + 0.1 × 1.05 × 1.15) – 1) × 100%, где 1 — начальные значения цен на три товара.
Зная эти два метода решения задач на проценты, вы сможете легко решать задачи как в повседневной жизни, так и на экзаменах.
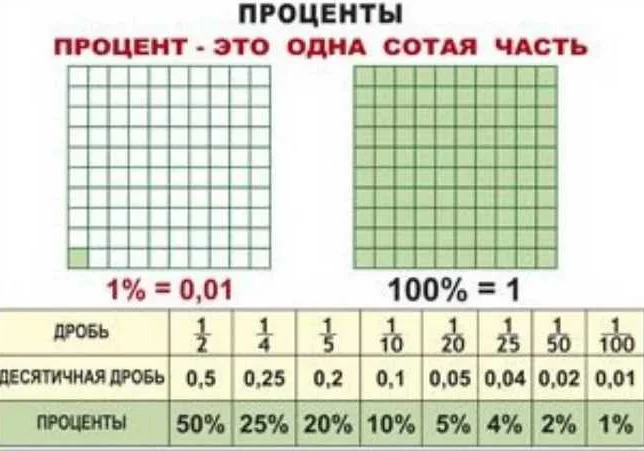
Таблицы процентов

Таблицы процентов представляют собой удобный инструмент для быстрого вычисления процентных значений. Такие таблицы состоят из двух столбцов: в первом указываются процентные значения от 1% до 100%, а во втором – соответствующие им десятичные значения (от 0,01 до 1).
Например, если нам нужно вычислить 20% от числа 200, мы можем обратиться к таблице процентов, найти строку с 20% в первом столбце и узнать, что соответствующее десятичное значение равно 0,2. Затем мы можем просто умножить число 200 на 0,2 и получить итоговое значение – 40.
Таблицы процентов также могут использоваться для обратного вычисления – если мы знаем процентное значение и итоговое значение, мы можем найти исходное число. Например, если мы знаем, что 25% от числа x равно 50, мы можем найти соответствующее десятичное значение в таблице процентов (0,25) и использовать формулу x = 50 / 0,25, чтобы получить исходное число – 200.
ПроцентДесятичное значение
| 1% | 0,01 |
| 2% | 0,02 |
| 3% | 0,03 |
| 4% | 0,04 |
| 5% | 0,05 |
| 10% | 0,1 |
| 15% | 0,15 |
| 20% | 0,2 |
| 25% | 0,25 |
| 50% | 0,5 |
| 75% | 0,75 |
| 100% | 1 |






