Нод — это наибольший общий делитель двух или более целых чисел. Расшифровка слова
Нод, сокращение от слова «наибольший общий делитель», является одним из основных понятий в математике. Он используется во многих областях, включая алгебру, теорию чисел и криптографию. Нод двух чисел — это наибольшее число, которое делится без остатка на оба числа.
Нод имеет множество применений, как в обычных вычислениях, так и в решении сложных задач. Также данный термин может быть выражен с помощью формул и алгоритмов вычисления, которые позволяют быстро определить наибольший общий делитель.
Понимание понятия нод является необходимым для работы с различными алгоритмами и вычислениями в математике, поэтому его изучение является важным компонентом образования для студентов.
Что такое НОД

НОД (наибольший общий делитель) — это математический термин, обозначающий наибольшее число, которое делит два или более других числа без остатка. Например, НОД для чисел 12 и 18 равен 6, потому что 6 является наибольшим числом, которое делит как 12, так и 18 без остатка.
НОД может быть найден путем факторизации чисел на простые множители и поиска общих множителей, которые встречаются в каждом числе. Кроме того, существуют алгоритмы, которые могут находить НОД быстрее, чем простой метод факторизации.
НОД используется во многих различных областях математики и науки, таких как теория чисел, алгоритмы, криптография, а также в решении уравнений и задач в геометрии.
Значение НОД в математических вычислениях
НОД – это аббревиатура от выражения «Наибольший Общий Делитель». В математике используется для нахождения наименьшего числа, которое делится на все заданные числа без остатка.
Для нахождения НОД двух или более чисел необходимо разложить каждое число на простые множители и вычислить произведение общих множителей с наименьшими показателями степеней. Если числа не имеют общих множителей, то их НОД равен единице.
Например, если необходимо найти НОД чисел 12 и 18, то сначала выражения разлагаются на простые множители: 12 = 2 * 2 * 3 и 18 = 2 * 3 * 3. Общие множители – 2 и 3 с наименьшими показателями степеней – 2 в первой и 1 во второй, и 3 в первой и 2 во второй. Произведение общих множителей равно 2 * 3 = 6, поэтому НОД(12, 18) = 6.
НОД также используется для нахождения НОК (Наименьшего Общего Кратного) двух и более чисел, которое выражается через их НОД с помощью формулы: НОК(a,b) = (a * b) / НОД(a,b).
НОД также применяется в теории чисел, алгебре, геометрии, теории вероятности и в других областях математики.
НОД как наибольший общий делитель
НОД (Наибольший общий делитель) — это число, которое является наибольшим делителем двух целых чисел без остатка. Например, наибольший общий делитель чисел 12 и 18 равен 6.
Чтобы найти НОД двух чисел, можно использовать различные методы, например:
-
- Метод вычитания: вычитаем меньшее число из большего до тех пор, пока они не станут равными. Например, для чисел 24 и 36:
- 36-24=12
- 24-12=12
- 12-12=0
- Метод деления: последовательно делим большее число на меньшее с вычислением остатка. НОД равен последнему ненулевому остатку. Например, для чисел 20 и 30:
- Метод вычитания: вычитаем меньшее число из большего до тех пор, пока они не станут равными. Например, для чисел 24 и 36:
ДелимоеДелительОстаток
| 30 | 20 | 10 |
| 20 | 10 | 0 |
НОД используется во многих математических задачах, например, для сокращения дробей, нахождения общего знаменателя, проверки взаимной простоты чисел и т.д.
Как вычислить НОД

Нахождение наибольшего общего делителя (НОД) двух чисел — это одна из базовых задач в теории чисел. НОД двух чисел a и b — это наибольшее целое число, которое делит оба числа без остатка.
Существует несколько методов для вычисления НОД, но одним из самых простых и эффективных подходов является алгоритм Евклида. Он основан на свойстве НОД(a,b) = НОД(b,a mod b), где «mod» обозначает операцию остатка от деления.
Применяя этот подход последовательно, можно вычислить НОД двух чисел за несколько итераций:
- Найти остаток от деления большего числа на меньшее: r = a mod b
- Если r = 0, тогда НОД равен меньшему числу: НОД(a,b) = b
- Если r не равен 0, тогда повторить алгоритм для пары (b, r)
Например, чтобы найти НОД чисел 36 и 24:
- 36 mod 24 = 12
- 24 mod 12 = 0, тогда НОД(36,24) = 12
Этот метод прост и довольно быстрый, работая за время O(log n), где n — максимальное из двух чисел. Он также может быть расширен на нахождение НОД для большего числа.
Алгоритм Евклида
Алгоритм Евклида – это математический алгоритм, который используется для нахождения наибольшего общего делителя двух целых чисел. НОД – это наибольшее число, которое делится без остатка на оба исходных числа.
Алгоритм Евклида используется уже более 2000 лет. Сейчас он является основой для многих других математических алгоритмов, таких как RSA и Euklid-Legendre.
Сам алгоритм очень простой. Для двух целых чисел a и b необходимо выполнять следующие действия:
- Делить большее число на меньшее.
- Если делится без остатка, то меньшее число и есть НОД.
- Если нет, то необходимо заменить большее число на остаток от деления и повторить шаг 1.
Этот процесс продолжается до тех пор, пока одно из чисел не станет равным 0. В этом случае НОД равен другому числу.
Например, посчитаем НОД для чисел 84 и 18:
- 84 / 18 = 4 (остаток 12)
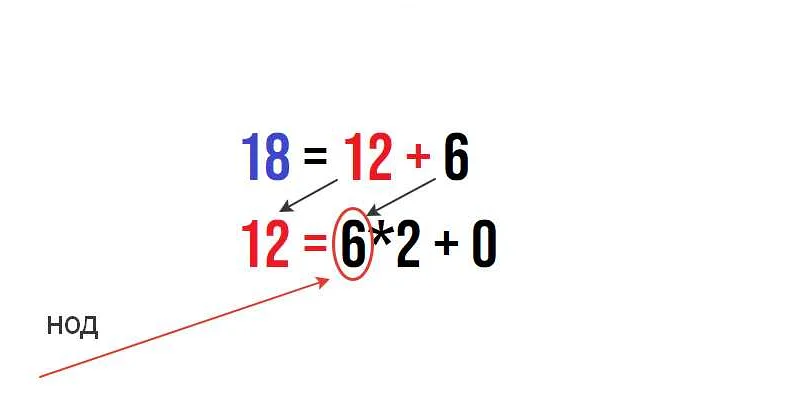
- 18 / 12 = 1 (остаток 6)
- 12 / 6 = 2 (остаток 0)
Таким образом, НОД для чисел 84 и 18 равен 6.
Алгоритм Евклида является очень эффективным и быстрым. Он может быть использован не только для целых чисел, но и для рациональных и даже комплексных чисел.
НОД и НОК
НОД (наибольший общий делитель) — это наибольшее число, которое является делителем двух или более целых чисел без остатка. Например, найти НОД чисел 12 и 16. Делители числа 12: 1, 2, 3, 4, 6, 12, а для числа 16: 1, 2, 4, 8, 16. Наибольшим делителем обоих чисел является 4. Символически, НОД(12, 16) = 4.
НОК (наименьшее общее кратное) — это наименьшее число, которое делится на два или более целых чисел без остатка. Например, найти НОК чисел 4 и 6. Кратым числа 4 являются: 4, 8, 12, 16, … Кратным числа 6 являются: 6, 12, 18, 24, … Наименьшим общим кратным является 12. Символически, НОК(4, 6) = 12.
Можно также использовать формулу: НОД(а, b) * НОК(а, b) = a * b. Зная НОД или НОК, можно вычислить другую величину, используя формулу. Например, если НОД чисел 18 и 24 равен 6, то НОК равен 18 * 24 / 6 = 72.
НОД и НОК используются в различных областях математики, например, в алгебре, теории чисел, геометрии и других. Они являются важными понятиями для решения задач на поиск общих кратных и делителей, факторизацию чисел и построение матриц.
Наибольший общий делитель полиномов
В математике, наибольшим общим делителем (НОД) двух или более чисел называется наибольшее число, которое делит каждое из данных чисел без остатка. Аналогично, в алгебре, наибольший общий делитель полиномов — это наибольший полином, который является делителем каждого заданного полинома.
Расчет НОД полиномов может быть выполнен несколькими способами, включая метод евклида и метод факторизации. Метод евклида основан на делении полинома на заданный полином, пока остаток не станет равен нулю. Метод факторизации затем использует разложение каждого полинома на простые множители, чтобы найти их общие множители и, следовательно, НОД.
Наибольший общий делитель полиномов имеет важное значение в решении уравнений и систем уравнений в алгебре. Он может использоваться для упрощения и сокращения дробей, решения уравнений и определения их корней, а также для вычисления интегралов и нахождения длины дуги кривой.
Как и в случае с НОД чисел, НОД полиномов имеет свои свойства, включая коммутативность, ассоциативность, идемпотентность, линейность и дистрибутивность, что делает его универсальным инструментом в алгебре и математике в целом.
Суть алгоритма Евклида для полиномов
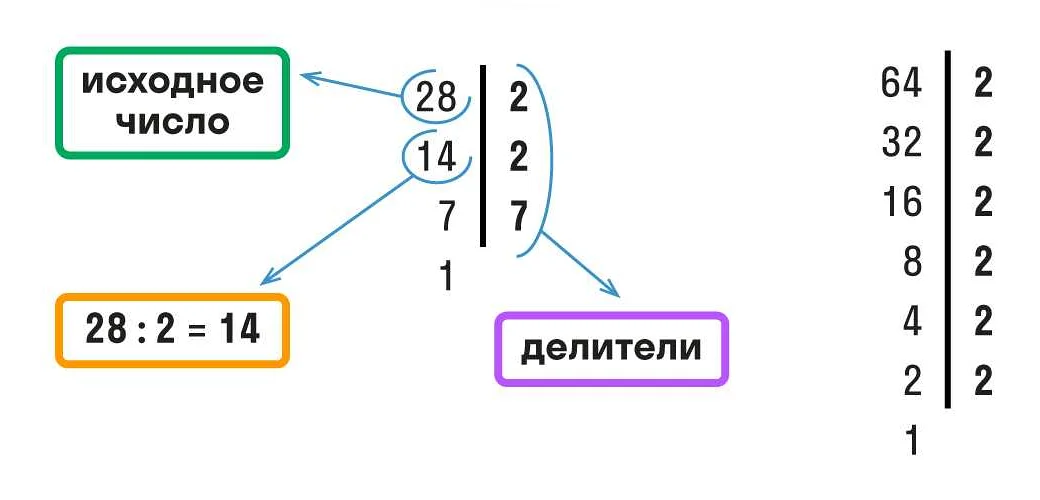
Алгоритм Евклида изначально был разработан для нахождения наибольшего общего делителя двух целых чисел. Однако этот алгоритм легко обобщается для полиномов. Суть алгоритма Евклида для полиномов заключается в последовательном делении многочленов на остаток.
Идея состоит в том, чтобы найти наибольший общий делитель двух полиномов путем последовательного деления одного полинома на другой с остатком. Таким образом, каждое последующее деление будет исходить не от изначальных полиномов, а от последнего остатка.
Процедура продолжается до тех пор, пока остаток не станет равным нулю. На этом этапе предыдущий делитель будет наибольшим общим делителем исходных полиномов.
Пример применения алгоритма Евклида для полиномов:
Даны полиномы f(x) = 5x^3 + 10x^2 + 15x + 20 и g(x) = 3x^2 + 6x + 9. Необходимо найти наибольший общий делитель двух полиномов.
ДелениеЧастноеОстаток
| f(x) / g(x) | 5x + 5 | 5x^2 + 5x + 20 |
| g(x) / (5x^2 + 5x + 20) | (1/5)x + (11/25) | 0 |
Таким образом, наибольший общий делитель равен g(x) = 3x^2 + 6x + 9.
Видео по теме:
Вопрос-ответ:
Что такое термин «Нод» в математических вычислениях?
Нод (наибольший общий делитель) — это наибольшее число, которое делит два или несколько чисел нацело, при этом само НОД также является целым числом.
Какие алгоритмы используются для нахождения НОД?
Существует несколько алгоритмов, таких как алгоритм Евклида, бинарный алгоритм и расширенный алгоритм Евклида.
Как работает алгоритм Евклида?
Алгоритм Евклида основан на том, что НОД двух чисел равен НОДу одного из них и остатка от деления второго на первое число. Этот процесс повторяется до тех пор, пока не будет найден НОД.
Какой алгоритм лучше использовать для больших чисел?
Для больших чисел лучше использовать расширенный алгоритм Евклида, который позволяет находить не только НОД, но и обратный элемент по модулю.
Как можно применять НОД в практических задачах?
Например, для упрощения дробей, поиска периодов десятичных дробей, проверки взаимной простоты чисел и т.д.
Можно ли использовать НОД для нахождения общего знаменателя?
Да, используя НОД, можно найти общий знаменатель для нескольких дробей, умножив каждую дробь на такой множитель, чтобы знаменатель каждой дроби был равен НОДу знаменателей.
Что такое расширенный алгоритм Евклида?
Расширенный алгоритм Евклида позволяет находить НОД двух чисел, а также коэффициенты Безу — числа, которые даются при разложении НОДа на данные числа. Эти коэффициенты могут использоваться для решения уравнений и систем уравнений.
Примеры расчета НОД для полиномов

НОД (наибольший общий делитель) для полиномов вычисляется аналогично НОД для целых чисел. Рассмотрим несколько примеров:
- Пример 1: Вычислить НОД для полиномов p(x) = x^2 – 4 и q(x) = x^2 – 1.
- Решение: Сначала запишем оба полинома в виде произведения множителей: p(x) = (x + 2)(x – 2), q(x) = (x + 1)(x – 1).
- Затем находим общие множители: (x + 2), (x – 2), (x + 1), (x – 1).
- НОД(p(x), q(x)) = (x + 1)(x – 1) = x^2 – 1.
- Пример 2: Вычислить НОД для полиномов p(x) = x^3 + 2x^2 – x – 2 и q(x) = x^2 – 1.
- Решение: Сначала проверим, является ли q(x) делителем p(x) при делении с остатком. Выполним деление с остатком: (x^3 + 2x^2 – x – 2) / (x^2 – 1) = x + 3 + (2x + 1) / (x^2 – 1).
- Таким образом, мы видим, что q(x) не является делителем p(x).
- Запишем оба полинома в виде произведения множителей: p(x) = (x + 1)(x – 1)(x + 2), q(x) = (x + 1)(x – 1).
- Затем находим общие множители: (x + 1), (x – 1).
- НОД(p(x), q(x)) = (x + 1)(x – 1) = x^2 – 1.
Применение НОД в криптографии
НОД (Наибольший Общий Делитель) является важной математической концепцией, которая применяется во многих областях, включая криптографию. В криптографии НОД используется для построения безопасных криптографических систем.
Одно из применений НОД в криптографии — это алгоритм Эвклида, который используется для генерации больших простых чисел. Большие простые числа используются для создания криптографических ключей, которые используются для зашифрования информации. Алгоритм Эвклида помогает создать большие простые числа, что делает систему шифрования более безопасной.
Другое применение НОД в криптографии — это алгоритм расширенного Евклида. Этот алгоритм используется для нахождения обратного элемента в кольце вычетов по модулю p, то есть для нахождения такого числа, при умножении на которое получится остаток 1 при делении на p. Это позволяет создавать криптографические ключи для симметричного шифрования.
НОД также используется для построения криптосистем, основанных на асимметричной криптографии, таких как RSA. В этих системах используется общедоступный ключ и закрытый ключ. При шифровании сообщения используется общедоступный ключ, а для расшифровки — закрытый ключ. Закрытый ключ вычисляется с помощью НОД и других математических операций.
Как видно из вышесказанного, НОД играет важную роль в криптографии и является необходимым инструментом для разработки безопасных криптографических систем. Без применения НОД криптографические системы не могли бы обеспечить необходимый уровень безопасности и защиты от несанкционированного доступа к конфиденциальной информации.






