Arccos (арккосинус) – это обратная функция косинуса, позволяющая найти угол, косинус которого равен заданному числу. Узнайте, как использовать arccos в математических расчетах.
Arccos (арккосинус) – это одна из тригонометрических функций, которая генерирует угол, косинус которого равен заданному значению. В математике, arccos используется для нахождения угла между двумя векторами в трехмерном пространстве, а также для решения уравнений, связанных с тригонометрией.
Arccos обычно обозначается как acos или cos ^ (-1) (читается как “арккос”), где ^ (-1) означает обратную функцию. Используя arccos, можно вычислить угол между двумя векторами, используя формулы тригонометрии, такие как теорема косинусов и теорема синусов.
Arccos также может использоваться для определения допустимого диапазона возможных значений для ряда функций. Например, при использовании формулы эйлеровой поворотной функции (euler rotation function), которая используется в компьютерной графике и анимации, arccos может использоваться для определения максимального угла поворота модели без искажения ее пропорций.
Определение
Arccos, или обратный косинус, является обратной функцией косинуса и обозначается как arccos(x). Она определяет угол, значение косинуса которого равно x. То есть, если cos(y) = x, то arccos(x) = y.

Функция arccos(x) определена только в интервале [-1,1], так как косинус может принимать значения от -1 до 1 включительно. Если переданный аргумент вне этого интервала, функция arccos(x) вернет ошибку.
Математически, arccos(x)=y означает, что x=cos(y) и y лежит в пределах [0, π]. Обратная функция косинуса имеет множество значений, поэтому часто используются уточняющие дополнительные ограничения, такие как arccos(x) ∈ [0, π] или arccos(x) ∈ [-π / 2, π / 2].
Ниже представлена таблица значений обратного косинуса:
xarccos(x)
| -1 | π |
| 0 | π / 2 |
| 1 | 0 |
Из таблицы видно, что arccos(x) является убывающей функцией на интервале [-1,1].
Видео по теме:
Примеры использования
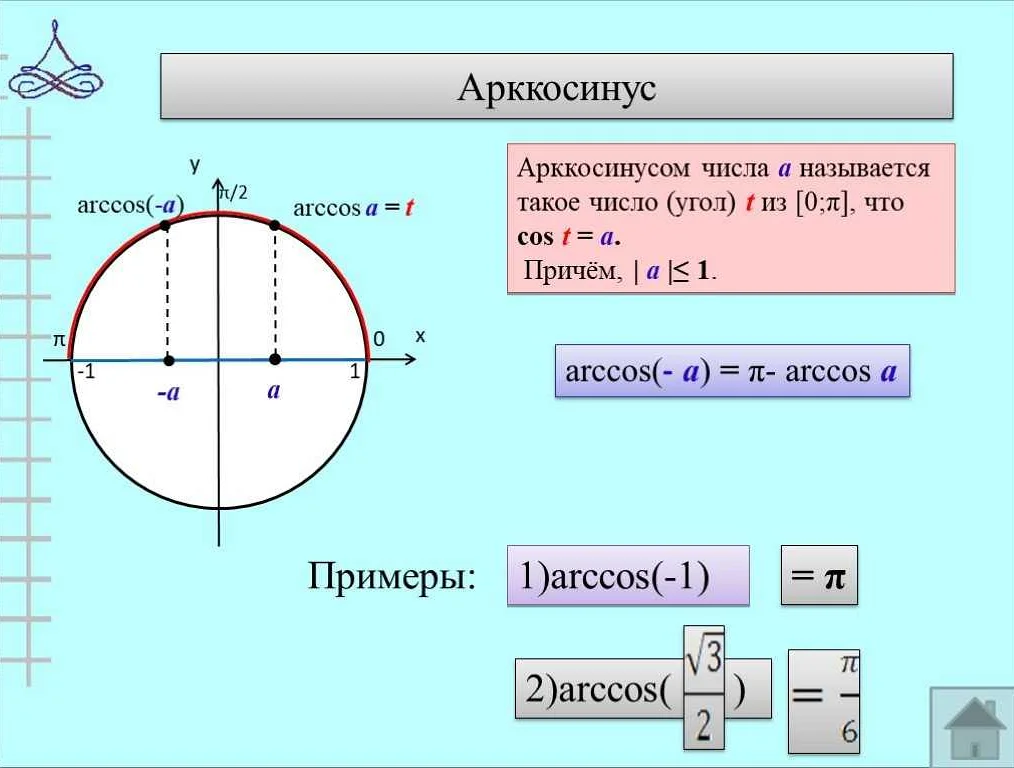
Функция arccos в математике может использоваться во многих различных задачах, особенно связанных с тригонометрией и геометрией. Ниже приводятся некоторые примеры использования:
-
- Нахождение угла между векторами: если даны два вектора в трехмерном пространстве, то угол между ними можно найти с помощью формулы, содержащей функцию arccos. Например, для векторов a и b:
cos(∠ab) = (a ⋅ b) / (|a| ⋅ |b|)
∠ab = arccos((a ⋅ b) / (|a| ⋅ |b|))
-
- Вычисление площади треугольника: если известны длины всех трех сторон треугольника, то его площадь можно найти с помощью формулы Герона. Однако, если известны длины двух сторон и угол между ними, то можно воспользоваться формулой для площади:
S = 0.5 ⋅ a ⋅ b ⋅ sin(∠ab)
S = 0.5 ⋅ a ⋅ b ⋅ sin(arccos((c^2 – a^2 – b^2) / (-2ab))))
-
- Разрешение уравнений: иногда функция arccos используется для разрешения уравнений в тригонометрии. Например, уравнение:
cos(x) = a
можно переписать как:
x = arccos(a) + 2πn
Кроме того, arccos может использоваться в других задачах, связанных с подобными треугольниками, определением расстояний и т.д.
Формула вычисления arccos

Функция arccos является обратной косинусной функцией. Она позволяет найти угол, косинус которого равен заданному значению. Формула вычисления arccos задается следующим образом:
arccos(x) = cos-1(x) = y
Здесь x является аргументом функции, а y – результатом. Функция arccos принимает значение от 0 до π включительно и возвращает угол в радианах.
Для вычисления arccos(x) можно использовать тригонометрические таблицы или калькулятор с функцией нахождения обратных тригонометрических функций. Также есть специальные формулы, которые позволяют вычислить arccos(x) аналитически. Например, можно воспользоваться формулой:
arccos(x) = π/2 – arcsin(x)
где x – значение, для которого необходимо найти угол.
Формула вычисления arccos находит свое применение в различных областях, включая физику, астрономию и 3D-графику. Она помогает определить угол между векторами, а также решать задачи на построение треугольников и нахождение углов и расстояний между точками.
Свойства функции arccos
Функция arccos является обратной косинусной функцией и по определению можно записать как: y = arccos x, где x какой-то из значений от -1 до 1, а y – угол в радианах в интервале от 0 до π (или от 0 до 180 градусов).
Свойства функции arccos:
- Область определения: -1 ≤ x ≤ 1, область значений: 0 ≤ y ≤ π (0 ≤ y ≤ 180 градусов).
- Симметрия: arccos (-x) = π – arccos x. Также arccos x = arccos (-x), если x = 1 или x = -1.
- Производные: arccos'(x) = -1 / sqrt(1 – x^2). Для доказательства можно воспользоваться формулой дифференцирования обратной функции.
- Интегралы: ∫(x, arccos(x)) dx = x * arccos(x) + sqrt(1 – x^2) + C
Функция arccos широко используется как инструмент для решения тригонометрических уравнений и задач геометрии. Также она может быть полезная в различных областях науки, включая физику и инженерию.
График функции arccos
Функция arccos – обратная функция косинуса и определена на отрезке [-1, 1]. График функции arccos – это график функции косинуса, отраженный относительно прямой y=x и затем повернутый на 90 градусов по часовой стрелке.
На графике функции arccos видно, что она монотонно убывает на отрезке [1, 0] и на отрезке [0, -1]. Минимальное значение функции равно pi, а максимальное – 0.
График функции arccos важен для определения аргумента косинуса, при котором косинус равен определенному значению. Например, если косинус аргумента равен 0.5, то соответствующий аргумент находится на пересечении графика функции косинуса и горизонтальной линии y=0.5, а значит, его значение можно найти, используя функцию arccos.
Таблица значений функции arccosxarccos(x)
| -1 | π |
| -0.5 | 2π/3 |
| 0 | π/2 |
| 0.5 | π/3 |
| 1 | 0 |
Различия между arccos и cos
cos – это функция, которая возвращает косинус угла, измеренного в радианах. Это означает, что она принимает угол в радианах и возвращает его косинус.
arccos – это обратная функция косинуса. То есть, если вы знаете значение косинуса угла, то arccos возвращает угол в радианах.
Одним из основных различий между этими функциями является их область определения. Функция cos имеет область определения (-∞, ∞), в то время как область определения функции arccos ограничена диапазоном от 0 до π.
Кроме того, эти функции имеют различные обратные функции. В случае cos обратной функцией является arccos, а для arccos обратной функцией является cos.
Наконец, стоит отметить, что эти функции также имеют различные графики. График функции cos – это периодическая функция, которая колеблется между значениями -1 и 1. График функции arccos в свою очередь – это немонотонная функция, которая имеет значения от 0 до π.
Применение arccos в реальной жизни
Arccos – это обратная функция косинуса. Одним из способов использования arccos является нахождение углов в прямоугольных треугольниках. В частности, arccos встречается при решении задач на комплексные числа, электротехнике, радиотехнике и многих других областях науки и техники.
В жизни мы также можем столкнуться с применением arccos. Например, если мы знаем коэффициент трения между двумя телами, мы можем использовать arccos для определения максимального угла наклона плоскости, при котором тело не начнет скользить. Также arccos может быть использован для определения максимального угла наклона дороги, при котором автомобиль не потеряет сцепление с дорогой и не начнет скользить.
Медики используют arccos для измерения телесной жировой массы (ТЖМ) у пациентов. С помощью arccos можно определить процент жира на теле человека, используя измерения окружности шеи и талии.
Arccos также широко используется в компьютерных играх и анимации. В играх, например, arccos используется для определения движения персонажа, когда он пересекает границу, а в анимации – для различных эффектов.
Таким образом, arccos является очень полезным математическим инструментом, который имеет множество применений в различных областях науки и техники, который мы встречаем не только в классной учебе, но и в повседневной жизни.
Возможные ошибки при использовании arccos

Arccos в математике – это функция обратная к косинусу. Она используется для нахождения угла, косинус которого равен заданному значению. Однако при использовании данной функции можно допустить ряд ошибок.
Ошибка 1: Неправильный диапазон значений. Arccos является многозначной функцией и имеет диапазон значений от 0 до π. Поэтому, если результат получился за пределами этого диапазона, то, скорее всего, была совершена ошибка в расчёте.
Ошибка 2: Использование радианов вместо градусов. При использовании арккосинуса, необходимо помнить, что он работает со значениями в радианах. Если же полученные значения заданы в градусах, необходимо их преобразовать.
Ошибка 3: Ввод отрицательного числа. Значение арккосинуса определено только для чисел в диапазоне от -1 до 1. При вводе отрицательного числа, функция выдаст ошибку.
Ошибка 4: Значение undefined. В некоторых случаях, при решении уравнений, функция arccos может не иметь определённого значения. Это происходит, например, когда косинус угла равен 1 или -1. В таких случаях, результат вычислений будет undefined.
Все указанные ошибки могут привести к неверным результатам и затруднить решение задачи. Поэтому, при использовании функции arccos, необходимо быть внимательным и учитывать все возможные нюансы, связанные с её работой.
Альтернативы функции arccos
Функция arccos (обратная косинус) является одной из тригонометрических функций, которые вычисляют угол между гипотенузой и прилегающим катетом прямоугольного треугольника.
Однако, существует также множество других функций, которые могут использоваться для вычисления углов. Например:
- arcsin – обратная синус функция, которая вычисляет угол между гипотенузой и противоположным катетом;
- arctan – обратная тангенс функция, которая вычисляет угол между прилегающим катетом и противоположным катетом;
- arccot – обратная котангенс функция, которая вычисляет угол между прилегающим катетом и гипотенузой;
- arcsec – обратная секанс функция, которая вычисляет угол между гипотенузой и прилегающим катетом при использовании секанс функции;
- arccsc – обратная косеканс функция, которая вычисляет угол между гипотенузой и противоположным катетом при использовании косеканс функции.
Стоит отметить, что выбор функции для вычисления угла зависит от конкретной задачи и условий ее решения. В некоторых случаях, функция arccos может быть неоптимальным выбором, и для более точного вычисления угла необходимо применять альтернативные функции.
Итоги и выводы
Arccos – это обратная функция косинуса, которая позволяет находить угол между гипотенузой и прилежащим катетом прямоугольного треугольника, зная значения косинуса.
Использование arccos часто возникает в задачах связанных с геометрией, тригонометрией, физикой, а также в программировании и компьютерной графике, где требуется точное вычисление угла.
Для решения задач связанных с нахождением углов, необходимо знать формулу arccos и способы работы с ней. Число, которое получим при вычислении arccos, в радианах, поэтому если требуется ответ в градусах, его необходимо перевести по формуле.
- arccos(0) = π/2
- arccos(1) = 0
- arccos(-1) = π
Вывод: arccos – это важная математическая функция, которая позволяет находить угол между гипотенузой и прилежащим катетом прямоугольного треугольника. Знание формулы и способов использования позволит легко решать задачи связанные с определением углов и точных вычислений в различных областях знаний.
Вопрос-ответ:
Для чего нужна функция arccos?
Функция arccos используется для нахождения угла, косинус которого равен заданному числу.
Какие значения принимает arccos?
Функция arccos принимает значения в диапазоне от 0 до π радиан или от 0 до 180 градусов.
Как вычисляется arccos?
Значение arccos может быть найдено с помощью обратной функции косинуса, то есть если cos(x) = y, тогда arccos(y) = x.
Какая формула используется для вычисления arccos?
Формула для вычисления arccos имеет вид: arccos(y) = x, где cos(x) = y. Также можно использовать формулу: arccos(y) = π/2 – arcsin(y).
Можно ли выразить arccos через другие функции?
Да, функция arccos может быть выражена через функции синуса и тангенса: arccos(y) = π/2 – arctan(y/√(1-y^2)).
Какое значение имеет arccos(0)?
Значение arccos(0) равно π/2 радиан или 90 градусов.
Как изменяется значение arccos при изменении аргумента?
Значение arccos убывает при увеличении аргумента от 1 до 0 и увеличивается при уменьшении аргумента от 0 до -1.






