Базис в дискретной математике – это набор элементов, который используется для описания других элементов в линейном пространстве. Примеры базисов, а также их свойства и применение в различных областях математики.
Базис – одно из ключевых понятий в алгебре и дискретной математике. Базисом называется набор элементов, который можно использовать для создания любого другого элемента данного пространства. В дискретной математике базис является основой для изучения любых комбинаторных систем.
В математике базисы широко используются в линейной алгебре, где они представляют собой набор линейно независимых элементов векторного пространства. В дискретной математике базисы используются для решения задач комбинаторного анализа, таких как графические модели сетей и комбинаторика.
Важно отметить, что базис дискретной математики может быть крайне мощным инструментом, который может помочь в решении различных задач. Поэтому понимание того, что такое базис в дискретной математике и для чего его использовать, является важным элементом практического применения дискретной математики.
Базис дискретной математики
Дискретная математика – это раздел математики, изучающий разные объекты, которые имеют дискретный (отдельный) характер. Она исследует объекты, которые разбиваются на отдельные составляющие, такие как числа, графы, комбинаторика и т.д.
В дискретной математике отдельные компоненты называются базисными элементами. Такие базисные элементы могут быть использованы для описания более сложных объектов.
Хорошим примером является базисные элементы в линейной алгебре. В линейной алгебре, комбинации векторов могут быть созданы из базисных векторов, которые являются линейно независимыми. Базис позволяет представить векторы в пространстве как линейную комбинацию их базисных элементов, что делает работу с ними гораздо проще.
Кроме линейной алгебры, базис дискретной математики находит свое применение в теории графов, комбинаторике и алгоритмах. В графах, базисными элементами могут быть отдельные ребра или вершины графа. В комбинаторике, базисы используются, чтобы получить все возможные комбинации элементов в заданном множестве.
Таким образом, базис дискретной математики является важным инструментом для работы в ряде математических дисциплин. Он предоставляет набор базисных элементов, которые могут быть использованы для создания более сложных объектов, что делает их изучение и анализ значительно более простым.
Что такое базис дискретной математики?
Базис дискретной математики является набором элементов, которые могут быть использованы для создания всех других элементов в данной системе. В отличие от непрерывной математики, где функции и переменные являются непрерывными, в дискретной математике элементы обычно ограничены конечным или счётным количеством.
Базис может быть наиболее простым и эффективным способом определения элементов в системе. В дискретной математике базис может быть набором логических операций или комбинацией символов, которые могут быть использованы для создания всех других символов в системе. Например, в бинарной системе (системе с основанием 2), базисом являются два символа — 0 и 1, которые могут быть использованы для создания всех других чисел.
Базисы широко используются в области теории кодирования, криптографии, теории графов и других областях дискретной математики. Например, в теории кодирования используется базис, состоящий из нескольких векторов, которые используются для создания всех остальных векторов в системе. Такой базис может быть использован для определения ошибок в передаче данных и их исправления.
Определение базиса в дискретной математике является важным шагом при разработке систем, так как он позволяет определить минимальный набор элементов, который может быть использован для создания всех других элементов в системе. Без базиса многие алгоритмы и схемы не могут быть реализованы.
Зачем нужен базис дискретной математики?
Дискретная математика — это раздел математики, который изучает дискретные объекты, такие как целые числа, графы, комбинаторные объекты и т.д. Один из основных инструментов дискретной математики – базис, который позволяет описывать дискретные объекты в терминах других объектов.
Базис дискретной математики необходим для решения многих задач в разных областях, в том числе при проектировании компьютерных программ, криптографии, теории кодирования и т.д. Базис позволяет свести сложную задачу к более простым дискретным объектам и подходам.
Базис дискретной математики также важен для развития мышления и логического мышления студентов, а также способствует развитию компетенций в области алгоритмического мышления и программирования.
В заключении, использование базиса дискретной математики помогает решать сложные задачи с помощью простых подходов и инструментов, а также развивает мыслительные процессы, которые могут быть использованы в других областях научного знания и практических применений.
Понятие “базис” в математике
Базис – это набор линейно независимых векторов, которые могут быть использованы для построения любого другого вектора в данном векторном пространстве. Другими словами, это набор векторов, из которых можно получить все остальные векторы в пространстве путем их линейной комбинации.
Для любого векторного пространства может существовать несколько базисов, но все они будут содержать одинаковое количество векторов, называемое размерностью. Если размерность пространства конечна, то все базисы будут иметь одинаковое количество векторов.
Базисы широко используются во многих областях математики, таких как линейная алгебра, теория чисел, дифференциальные уравнения, анализ и т.д. Они являются основным инструментом для изучения и работ с векторами в пространствах различных размерностей.
Важно отметить, что базис не является уникальным для данного векторного пространства, и может меняться в зависимости от выбора векторов. Однако, любые два базиса будут эквивалентны, что означает, что они будут содержать одинаковое количество векторов и все векторы в одном базисе могут быть выражены через векторы другого базиса.
Виды базисов в математике

В математике используются различные виды базисов, которые являются фундаментальной частью в алгебре, геометрии, теории вероятностей и т.д.
Ортонормированный базис – это базис векторного пространства, состоящий из ортогональных векторов, имеющих единичную длину. Он часто используется в линейной алгебре и осуществляет переход между координатными системами.
Базис Грассмана – это базис в пространствах Грассмана, которые состоят из многочленов, множества и других алгебраических структур. Он используется для решения задач в теории групп, комбинаторике и математической физике.
Канонический базис – это базис в пространстве N-мерных векторов, который состоит из векторов, имеющих координаты, равные нулю кроме одной, которая равна единице. Он используется для представления линейных операторов и матриц в однородной форме.
Шаблонный базис – это базис в гильбертовом пространстве, который состоит из векторов, полученных из одного начального вектора с помощью применения некоторого линейного оператора. Он используется для решения задач в квантовой механике и теории информации.
Целый ряд базисов используется в различных областях математики и науки. Выбор и использование того или иного базиса зависит от типа задачи, которую необходимо решить, и особенностей конкретной области науки.
Базис в линейном пространстве
Базис в линейном пространстве – это набор векторов, которые образуют линейно-независимую систему и которые могут быть использованы для порождения любого другого вектора. Базис может быть установлен в любом линейном пространстве, независимо от его размерности и свойств.
Для того чтобы найти базис необходимо выбрать линейно-независимую систему векторов, которая может породить все элементы линейного пространства, а затем упорядочить эту систему. Элементы базиса называются базисными векторами, а число базисных векторов – размерностью линейного пространства.
Базис имеет множество свойств, например, любой вектор из линейного пространства может быть выражен линейной комбинацией базисных векторов. Кроме того, любое линейно-независимое множество векторов может быть дополнено до базиса.
Базис является важным понятием в линейной алгебре и имеет множество применений в математике и науке в целом. Например, базис используется при решении систем линейных уравнений, в определении матриц и тензоров, а также в построении графиков и фракталов.
Базис в комбинаторике
Базисом в комбинаторике называется набор объектов, из которых можно составить любой другой объект данного класса. Например, базисом для класса перестановок из n элементов является множество всех транспозиций (пар переставляемых элементов).
Базисы широко используются в комбинаторике для решения задач, связанных с перечислением и построением объектов. Они позволяют выразить любой объект данного класса через комбинации элементов базиса.
Базисы могут быть различными в зависимости от выбранного класса объектов. Например, базисом для класса подмножеств множества из n элементов может служить любой из трех наборов: множество всех одноэлементных подмножеств, множество всех подмножеств с фиксированным числом элементов, или множество всех двоичных векторов длины n.
Для некоторых классов объектов можно выбрать «естественный» базис, который позволяет более эффективно решать задачи. Например, для класса графов естественным базисом является множество всех остовных деревьев, которые можно использовать для нахождения количества различных графов данного размера.
Базисы также используются в алгебре и линейной алгебре, где они служат для задания пространства, натянутого на заданный набор векторов.
Базис в теории графов
Базис в теории графов – это минимальный набор деревьев, который может породить все остальные деревья графа. Если рассматривать граф как матрицу смежности, то базис можно определить как множество столбцов этой матрицы, которые образуют матрицу в общем случае невырожденной.
Базис может использоваться для различных задач, таких как поиск кратчайшего пути в графе, вычисление определителя матрицы смежности и т.д. Кроме того, базис в теории графов относится к понятию “линейной независимости”, что является важной концепцией линейной алгебры.
Диаметр графа – это максимальное расстояние между двумя вершинами графа. Базис может помочь найти диаметр графа – для этого нужно выбрать любые две вершины и вывести наименьшее дерево, которое связывает их. Это дерево будет содержать все кладбища графа и кратчайшие пути между всеми парами вершин.
Также базис может использоваться для поиска моста в графе – для этого нужно проверить, может ли дерево, порожденное базисом, существенно измениться при удалении одной из ребер. Если может, то это ребро является мостом.
Базис – это важное понятие в теории графов и широко используется не только в теории графов, но и в математике в целом. Он помогает в решении различных задач и является основой для других понятий, связанных с линейной алгеброй и теорией графов.
Видео по теме:
Вопрос-ответ:
Что такое базис в дискретной математике?
Базис в дискретной математике – это некоторое множество векторов, которые могут быть использованы для построения любого другого вектора в данном пространстве. Он используется для описания и анализа линейных пространств в дискретной математике.
Как определить, что множество является базисом в дискретной математике?
Чтобы множество векторов стало базисом, необходимо, чтобы векторы были линейно независимыми (ни один вектор не может быть выражен через линейную комбинацию других векторов) и они были способны порождать всё пространство.
Какую роль играет базис в дискретной математике?
Базис является одним из основных понятий в линейной алгебре, он играет ключевую роль в анализе линейных пространств. Базисное представление позволяет легче решать задачи по линейной алгебре, такие как вычисление матриц и решение систем линейных уравнений.
Как найти базис данного линейного пространства в дискретной математике?
Для того, чтобы найти базис линейного пространства, необходимо найти линейно независимые векторы, которые являются исходными векторами. Затем, эти векторы нужно дополнить другими векторами, которые могут порождать все векторное пространство данного набора.
Может ли базис дискретной математики быть бесконечным?
Да, базис дискретной математики может быть бесконечным. Например, в пространстве многочленов существует бесконечное количество векторов, которые могут быть использованы в качестве базиса. Но при их использовании возможны трудности с вычислениями. Большинство задач прибегают к использованию конечных базисов.
Каково соотношение базиса и размерности в дискретной математике?
Размерность линейного пространства – это количество векторов в его базисе. С другой стороны, любые два базиса линейного пространства имеют одинаковую длину, называемую размерностью пространства.
Базис в теории кодирования
В теории кодирования базисом называется набор символов, из которых строятся кодовые слова. Простейшим примером базиса является двоичный базис, состоящий из символов 0 и 1. Базис может быть более сложным, например, для кодирования текста использовать алфавит букв.
Наличие базиса позволяет строить различные коды с разной степенью надежности и производительности. Использование базиса также позволяет избежать коллизий в кодах, когда две разные комбинации символов дают одинаковый код.
Важной задачей в теории кодирования является построение оптимального базиса, который бы максимально уменьшал размер кода и обеспечивал его надежность. Для этого используются различные методы, включая алгоритмы Хаффмана и Шеннона-Фано.
Другим подходом к оптимизации базиса является использование кодовых слов переменной длины, где наиболее часто встречающиеся символы кодируются меньшим количеством бит, а редко использующиеся символы – большим количеством бит.
Важно помнить, что выбор базиса и метод его оптимизации зависит от конкретной задачи и требований к кодированию. Например, при кодировании аудио и видео данные часто используют базис ДКП (дискретное косинусное преобразование), который обеспечивает эффективное сжатие данных при сохранении качества звука и изображения.
Примеры применения базисов в дискретной математике
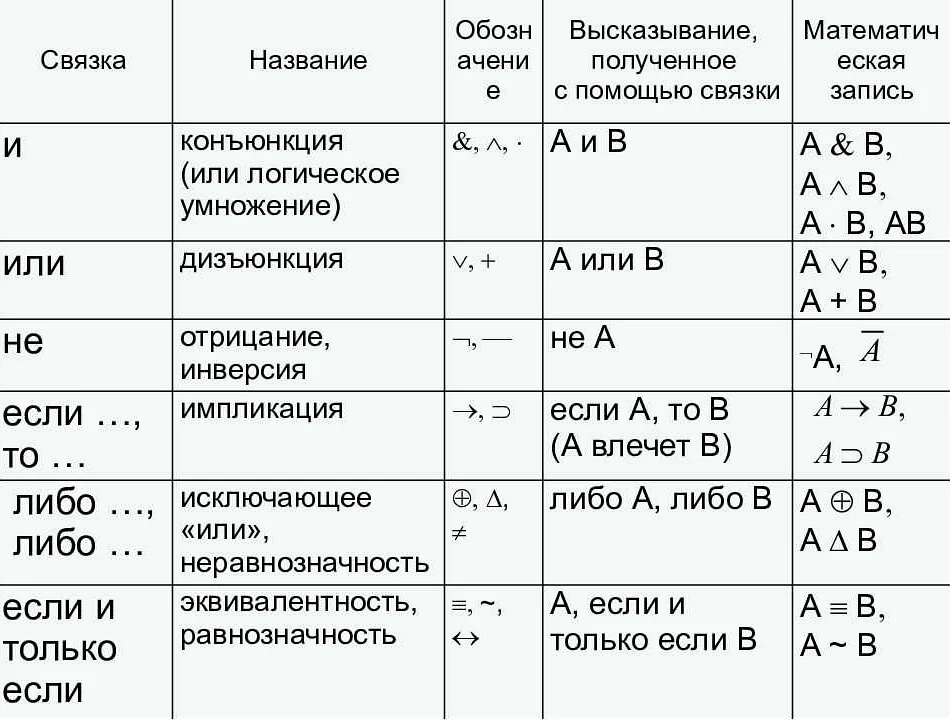
Базисы являются важным инструментом в дискретной математике и находят применение в различных ее областях.
- Логические функции: вместо использования множества переменных, логические функции могут быть выражены в терминах базиса, таких как AND, OR, NOT. Это позволяет проводить упрощения выражений и улучшать их производительность.
- Теория графов: базисы используются для описания графов и решения различных задач, таких как поиск максимального потока и минимального разреза в сети.
- Криптография: базисы применяются для шифрования и дешифрования информации. Один из примеров – шифр AES (Advanced Encryption Standard), использующий в качестве базиса операции над конечным полем.
- Кодирование: базисы используются для создания различных кодов, таких как коды Хэмминга и коды Рида-Соломона. Это позволяет обеспечить коррекцию ошибок и улучшить качество передачи данных.
Это лишь несколько примеров того, как базисы находят применение в дискретной математике. Они являются фундаментальным инструментом и помогают упрощать сложные задачи и улучшать производительность в различных областях.






