Буква i в математике обозначает мнимую единицу, которая используется в комплексных числах. Она равна квадратному корню из -1 и является ключевым элементом в алгебре и теории чисел.
Математика – точная наука, которая многим кажется слишком сложной и непонятной. В математике часто используются различные символы и обозначения, которые могут вызывать затруднения у студентов и учеников. Одним из таких символов является буква i, которая имеет важное значение в математических вычислениях.
Буква i используется для обозначения мнимых чисел – чисел, которые не могут быть представлены на числовой прямой. В обычной арифметике все числа являются действительными, то есть могут быть представлены точками на числовой прямой. Однако, в комплексной арифметике используются числа, которые состоят из вещественной и мнимой частей.
Таким образом, буква i обозначает мнимую единицу, которая равна квадратному корню из -1. Без буквы i невозможно было бы описать многие явления и процессы в физике, инженерии, экономике и других областях науки.
Что означает буква i в математике
Буква i в математике обозначает мнимую единицу. Это число, которое равно квадрату -1. Хотя мнимые числа могут показаться абстрактными или некоторым образом не реальными, они являются необходимыми для решения ряда математических проблем, включая уравнения второй степени, где их использование позволяет получить комплексные корни.
Часто буква i используется в комплексной алгебре. Комплексные числа содержат в себе как реальную, так и мнимую часть, выраженные как a+bi, где a и b – это любые действительные числа, а i – мнимая единица. Эти числа могут быть использованы в теории поля, физике и других областях математики.
Несмотря на то, что буква i в математике может показаться замысловатой и необычной обозначением, она является основой для решения многих задач и играет важную роль в различных областях математики и науки в целом.
Комплексные числа и буква i
Буква i в математике обозначает комплексную единицу. Комплексное число состоит из действительной и мнимой частей, которые могут быть записаны в виде a+bi, где a и b – действительные числа, а i – комплексная единица.
Комплексные числа используются в различных областях математики, физики и инженерии. Например, они используются для описания электрических цепей, расчетов в теории колебаний и многих других задач.
Кроме того, комплексные числа имеют множество интересных свойств и приложений. Например, они могут быть использованы для решения уравнений, в теории вероятности, теории серии Фурье и др.
Некоторые сочетания комплексных чисел с буквой i могут быть записаны в упрощенном виде. Например, i² = -1, i³ = -i, i⁴ = 1 и т.д. Эти свойства часто используются при расчетах с комплексными числами.
В заключение, комплексные числа с буквой i – это мощный и основополагающий инструмент в математике и других областях науки. Использование комплексных чисел позволяет эффективно решать сложные задачи и находить новые решения для различных проблем.
Демонстрация комплексных чисел
Комплексные числа имеют форму a + bi, где a и b – действительные числа, а i – мнимая единица, которая определяется как i * i = -1. Для наглядной демонстрации понятия комплексных чисел, можно представить их в виде точек на координатной плоскости – действительная часть на оси X, мнимая часть на оси Y.
Изображение комплексного числа на координатной плоскости называется комплексным числом-вектором (также известным как Argand-диаграмма). Например, число 3 + 4i представлено в виде точки с координатами (3,4) в Argand-диаграмме.
Комплексные числа также могут быть использованы для решения уравнений, для работы с контурным интегралом и другими приложениями в физике и инженерии. Их свойства могут быть изучены в математическом анализе.
- Таблица свойств комплексных чисел:
- – Сложение: (a + bi) + (c + di) = (a + c) + (b + d)i
- – Вычитание: (a + bi) – (c + di) = (a – c) + (b – d)i
- – Умножение: (a + bi) * (c + di) = (ac – bd) + (ad + bc)i
- – Деление: (a + bi) / (c + di) = (ac + bd) / (c2 + d2) + (bc – ad)i / (c2+d2)
- – Модуль: |a + bi| = √(a2 + b2)
Комплексные числа в технике и науке
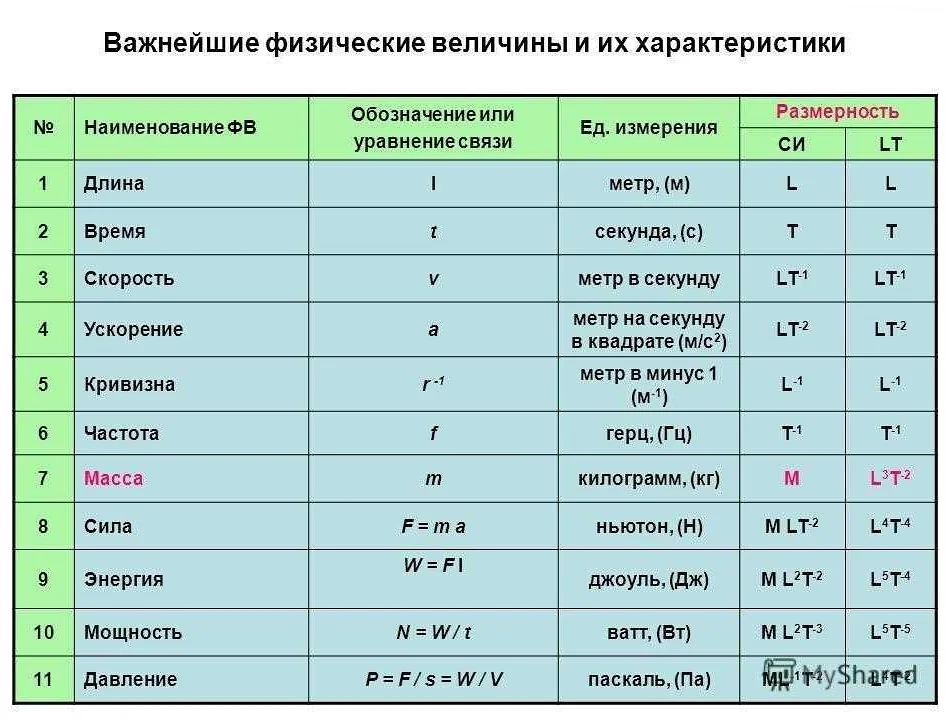
Комплексные числа представляют собой числа в формате a + bi, где a и b – это вещественные числа, а i – это мнимая единица. Комплексные числа первоначально возникли в математике, но в настоящее время они широко используются в технике и науке.
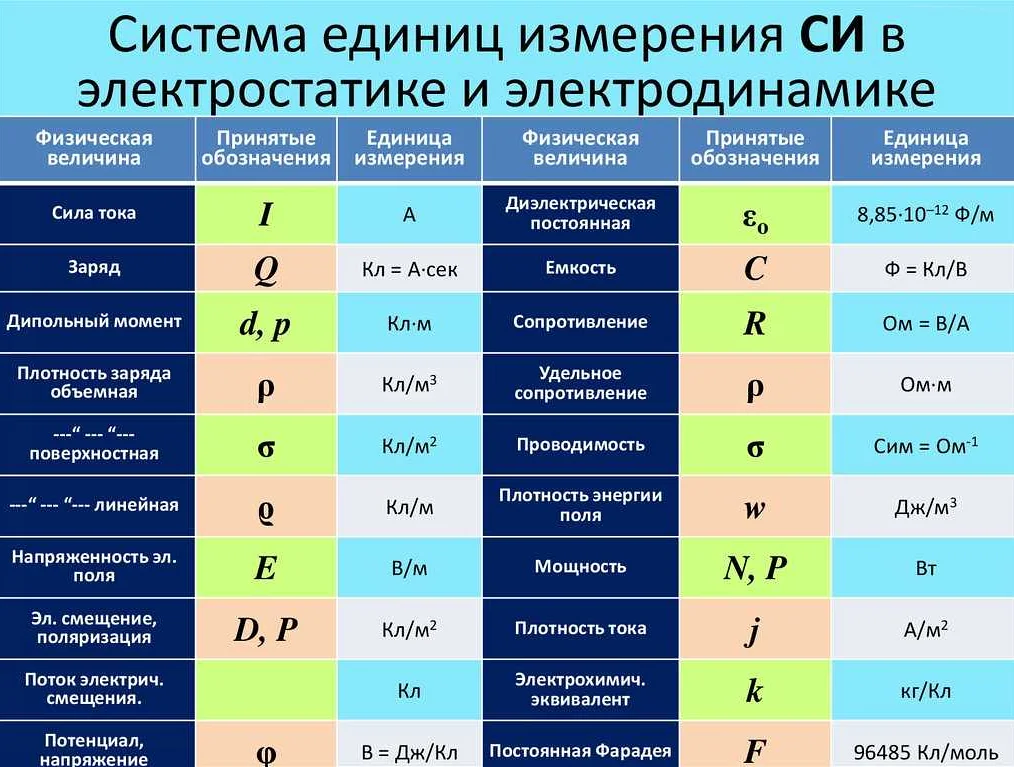
Одно из самых практически значимых применений комплексных чисел – это в электротехнике. В компьютерных сетях, например, используется модуль комплексной импедансии для описания электрических цепей. Комплексные числа также используются для моделирования дополнительных измерений, например, вращения искажений изображения в компьютерной графике.
В физике комплексные числа помогают описывать волновые процессы, такие как распространение света, звука и квантовых волновых функций. Они также используются в механике, особенно в области динамики и вибраций.
В целом, комплексные числа играют важную роль во многих областях науки и техники. Они помогают упростить математические вычисления и обеспечивают точное описание физических процессов.
Применение комплексных чисел в физике
Комплексные числа – это числа, которые включают в себя вещественную и мнимую компоненты и записываются в виде a + bi, где a и b – вещественные числа, а i – мнимая единица (i2 = -1).
В физике комплексные числа широко используются для решения задач, связанных с колебаниями, волнами и электричеством. Например, они используются для описания амплитуды и фазы колебаний в электронных цепях, которые используются в компьютерах.
Комплексные числа также используются для описания электромагнитных волн. Когда электромагнитная волна проходит через среду, ее амплитуда и фаза могут изменяться. Эти изменения могут быть описаны комплексными числами.
Кроме того, комплексные числа используются для описания волновых функций в квантовой механике. Волновые функции описывают состояния атомов и молекул и используются для предсказания их поведения в различных условиях. Квантовая механика – это важная область физики с множеством практических применений, таких как создание новых материалов и лекарств.
Выводы: комплексные числа играют важную роль в физике и используются для решения многих задач, связанных с колебаниями, волнами, электричеством и квантовой механикой.
Действия с комплексными числами

Комплексные числа представляют собой числа вида a + bi, где a и b – действительные числа, а i – мнимая единица, определяемая соотношением i² = -1.
Для выполнения арифметических операций с комплексными числами мы складываем или вычитаем их действительные и мнимые компоненты отдельно.
Например, для сложения комплексных чисел (a + bi) и (c + di) мы складываем их действительные и мнимые компоненты отдельно:
- Реальная часть: a + c
- Мнимая часть: b + d
Таким образом, сумма комплексных чисел будет (a + c) + (b + d)i.
Аналогично, для вычитания комплексных чисел мы вычитаем их действительные и мнимые компоненты отдельно:
- Реальная часть: a – c
- Мнимая часть: b – d
Таким образом, разность комплексных чисел будет (a – c) + (b – d)i.
Другие арифметические операции над комплексными числами, такие как умножение и деление, выполняются с учетом правил умножения и деления мнимой единицы i: i² = -1.
Умножение комплексных чисел (a + bi) и (c + di) выполняется следующим образом:
| a | bi | |
| c | ac | bci |
| di | adi | -bd |
Таким образом, произведение комплексных чисел будет (ac – bd) + (ad + bc)i.
Деление комплексных чисел (a + bi) и (c + di) выполняется путем умножения числителя и знаменателя на комплексно сопряженное число (c – di) и последующим упрощением:
(a + bi) / (c + di) = (a + bi)(c – di) / (c + di)(c – di) = [(ac + bd) + (bc – ad)i] / (c² + d²)
Таким образом, результатом деления комплексных чисел будет (ac + bd) / (c² + d²) + (bc – ad) / (c² + d²)i.
Важно отметить, что операции с комплексными числами могут быть выполнены с использованием формул Эйлера или тригонометрической формы, что упрощает вычисления в определенных случаях.
Корни из отрицательных чисел

Когда мы говорим о корнях в математике, мы обычно подразумеваем положительные числа. Но что если нам нужно извлечь квадратный корень из отрицательного числа?
В этом случае, мы обращаемся к комплексным числам. Комплексные числа имеют две части: действительную и мнимую. Обозначение мнимой единицы – i.
Когда мы извлекаем корень степени 2 из отрицательного числа a, то получаем комплексное число a*i. Например, квадратный корень из -4 равен 2i, так как (2i)² = 4*(-1) = -4.
Важно заметить, что квадрат комплексного числа a*i равен -a². Это свойство можно использовать для перемножения комплексных чисел.
В математике, комплексные числа играют важную роль не только в извлечении корней из отрицательных чисел, но и в различных областях, таких как электротехника, физика и теория чисел.
Решение квадратных уравнений
Квадратным уравнением называется уравнение вида ax2 + bx + c = 0, где a, b, c – коэффициенты, причем a ≠ 0.
Для решения квадратного уравнения существует формула, называемая формулой Квадратного корня:
x1,2 = (-b ± √(b2 – 4ac)) / 2a
Таким образом, чтобы найти корни квадратного уравнения, необходимо:
- Вычислить дискриминант – D = b2 – 4ac;
- Если D > 0, то уравнение имеет два корня x1 и x2, которые находятся по формуле Квадратного корня;
- Если D = 0, то уравнение имеет один корень x = -b / 2a;
- Если D < 0, то уравнение не имеет решений.
Правильное решение квадратного уравнения является базовой задачей, которую необходимо знать для подготовки к дальнейшим урокам математики.
Видео по теме:
Вопрос-ответ:
Зачем в математике используют букву i?
Буква i используется в математике для обозначения мнимой единицы. Это позволяет работать с комплексными числами, которые имеют две составляющие: действительную и мнимую. Математики используют букву i в формулах для вычисления различных функций и операций с комплексными числами.
Какие свойства имеет мнимая единица i?
Мнимая единица i обладает несколькими свойствами, которые позволяют работать с ней в математических выражениях. Во-первых, i возводится в квадрат, он даёт -1. Во-вторых, комплексное число вида a + bi можно выразить в виде a + ib, где a и b – это действительные числа. Также существует свойство сопряжения комплексных чисел, которое позволяет быстро вычислять обратное число и множественное деление.
В каких областях науки используется буква i?
Буква i используется не только в математике, но и в различных научных областях, таких как физика, электроника, инженерия и др. Например, в физике i используется в формулах для вычисления электромагнитных полей и волн, а в электронике – для определения импеданса электрических цепей. Кроме того, буква i связана с теорией вероятностей и квантовой механикой.
Как вычислять комплексные числа с использованием буквы i?
Для вычисления комплексных чисел с использованием буквы i нужно учитывать несколько правил. Например, чтобы сложить два комплексных числа, нужно сложить их действительные и мнимые части отдельно. А чтобы умножить два комплексных числа, нужно перемножить их действительные части и мнимые части отдельно, затем вычислить сумму произведений. Также существуют формулы для нахождения сопряженного числа, модуля и аргумента комплексного числа.
Какую роль играют комплексные числа в математике и её применениях?
Комплексные числа играют очень важную роль в математике, так как позволяют решать многие задачи, которые невозможно решить с помощью действительных чисел. Они находят применение в физике, электронике, теории вероятностей, криптографии и других областях. Без комплексных чисел не было бы возможности развития теории функций, которая является основой современной математики.
Как выглядят графики комплексных функций?
Графики комплексных функций имеют свойства, отличные от графиков функций одной переменной. Они изображаются на комплексной плоскости, где ось абсцисс соответствует действительной оси, а ось ординат – мнимой оси. Например, график функции sin(z) представляет собой бесконечную спираль вокруг начала координат, а график функции e^z – систему линий, параллельных действительной оси. Комплексные функции могут иметь разнообразные формы и требуют особого подхода при их исследовании.
Как связаны геометрия и комплексные числа?
Геометрия и комплексные числа тесно связаны между собой, так как каждое комплексное число можно представить как точку на плоскости. Модуль комплексного числа соответствует расстоянию от него до начала координат, а аргумент комплексного числа – углу между осью абсцисс и лучом, соединяющим начало координат с точкой на плоскости. С помощью комплексных чисел можно решать геометрические задачи, а также изучать свойства фигур и преобразований на плоскости.
Комплексные числа и тригонометрия
Комплексные числа – это числа, которые состоят из действительной и мнимой частей. Действительную часть часто обозначают буквой Re, а мнимую – буквой Im.
В тригонометрии комплексные числа играют важную роль. Комплексные числа могут быть представлены в виде модуля и аргумента. Модуль комплексного числа – это расстояние от начала координат до точки, в которой находится число.
Аргумент комплексного числа – это угол между осью Ox и лучом, исходящим из начала координат и проходящим через точку, в которой находится число. Аргумент может быть выражен в радианах или градусах и может быть положительным или отрицательным.
Комплексные числа используются в тригонометрии для работы с синусами и косинусами. Так, любое комплексное число может быть записано в виде:
- a + bi
- r(cosθ + i sinθ)
где a и b – действительная и мнимая части числа соответственно, r – модуль числа, а θ – аргумент числа. Формула r(cosθ + i sinθ) называется тригонометрической формой записи комплексного числа.
Благодаря комплексным числам в тригонометрии возможно решение многих задач, включая решение уравнений со сферическими функциями и переход от функций, определенных на одной окружности, к функциям, определенным на другой.
Использование комплексных чисел в алгебре
Комплексные числа – это числа, содержащие в себе как действительную, так и мнимую часть. Обозначаются они в общем виде как a + bi, где a и b – действительные числа, а i – мнимая единица, квадрат которой равен -1.
Использование комплексных чисел расширяет возможности алгебры. Они позволяют решать задачи, которые невозможно было бы решить при использовании только действительных чисел. Например, комплексные числа помогают в решении уравнений, которые имеют отрицательный дискриминант, а также позволяют решать системы линейных уравнений в комплексных коэффициентах.
Кроме того, комплексные числа используются в различных областях науки и техники, таких как электротехника, квантовая механика, оптика и другие.
Существует различные операции с комплексными числами, такие как сложение, вычитание, умножение и деление. Кроме того, в алгебре комплексные числа используются для определения функций и операторов, таких как комплексное сопряжение, модуль комплексного числа, тригонометрический вид комплексного числа.
Таким образом, использование комплексных чисел в алгебре является важным инструментом для расширения математических возможностей и решения задач в различных областях науки и техники.






