Прямые скобки в математике 6 класс обозначают группировку и порядок выполнения операций. Узнайте, как правильно использовать прямые скобки для решения задач с числами и переменными.
В математике 6 класса прямые скобки могут часто встречаться как в учебнике, так и на доске в классе. Но что они обозначают и как с ними работать?
Прямые скобки в математике использованы для обозначения округления до сотых или тысячных и могут стоять как вокруг отдельного числа, так и вокруг выражения. Они будут выглядеть так: [ ]. Например, [3.14159] означает, что необходимо округлить число до сотых.
Важно понимать, что при округлении до сотых, необходимо посмотреть на следующую цифру после запятой. Если она меньше 5, то число остаётся без изменений, а если 5 и больше, то число округляется в большую сторону. Например, число 3.145 станет 3.15, а число 3.144 будет 3.14.
Основное понятие
Прямые скобки – это символы, которые используются в математике для обозначения группировки выражений и операций, которые нужно выполнить в первую очередь. Они также могут использоваться для обозначения массивов и элементов массивов в программировании.
Пример использования:
- Выражение 2 * (3 + 4) можно записать как 2 * [3 + 4], чтобы показать, что сначала нужно выполнить операцию внутри скобок.
- В языке программирования Python можно использовать прямые скобки для создания списка: my_list = [1, 2, 3, 4, 5].
Кроме того, прямые скобки могут быть вложенными, то есть одни скобки могут находиться внутри других. В этом случае, операции внутри наименьших скобок выполняются в первую очередь, затем в более крупных, и так далее.
Пример: В выражении 4 * [2 + (3 + 1)] нужно сначала выполнить операцию в скобках, затем в квадратных скобках, а потом умножить на 4.
Значение скобок в знаках арифметических действий

В математике скобки используются для определения порядка выполнения действий. Круглые скобки означают, что содержимое в них должно быть выполнено первым. Например, в выражении (2 + 3) x 4 нужно выполнить операцию внутри скобок первой, и только потом умножать на 4, получим результат 20.
В отличие от круглых скобок, квадратные скобки используются для определения значения всего выражения внутри них. Они используются для обозначения индекса, то есть порядковой позиции внутри массива или матрицы. Например, [4, 5] означает элемент в четвертом ряду и пятом столбце.
Угловые скобки, такие как < >, используются для обозначения операторов, которые воспринимаются компьютером. Например, для условного оператора “if (условие)” используется символ < вначале и символ > в конце.
Все виды скобок могут быть использованы вместе в сложных математических выражениях, таких как ([2 + 3] x 4) < 5.
В контексте математики 6 класса, прямые скобки обычно не используются. В школьной программе обычно рассматриваются основные операции: сложение, вычитание, умножение и деление. Важно понимать значение скобок для правильного выполнения этих операций.
Отрицательные числа в скобках

В математике почти все числа можно записать как положительные величины. Однако существуют так называемые отрицательные числа, которые могут быть записаны со знаком “минус”. Такие числа могут быть также записаны в скобках, чтобы обозначить отрицательность числа.
Например, число “-5” может быть записано как “(-5)” для того, чтобы явно указать его отрицательность. Это особенно полезно при выполнении математических операций с отрицательными числами, чтобы избежать ошибок и упростить вычисления.
Кроме того, в некоторых математических выражениях скобки употребляются для задания порядка выполнения операций. Например, выражение (3 + 2) * 4 должно быть вычислено, сначала складывается 3 и 2 в скобках, а затем полученное значение умножается на 4.
Помимо скобок, отрицательные числа могут быть записаны в математических выражениях с помощью знака минус перед числом, например “-7”. Важно помнить, что знак минус перед числом указывает на отрицательность числа, а не на операцию вычитания.
В заключение, использование скобок для записи отрицательных чисел в математике имеет свои преимущества, особенно при выполнении математических операций с отрицательными числами. Знание этого правила поможет сделать вычисления более точными и упростить математические задачи.
Сокращение выражений с одинаковыми скобками
Прямые скобки в математике используются для выделения группы термов, которые следует рассматривать вместе. В выражениях могут встречаться одинаковые скобки, что позволяет выполнять их сокращение.
Для того чтобы выполнить сокращение, необходимо раскрыть скобки и умножить результат на коэффициент перед скобкой. Следующий пример поможет лучше понять этот процесс:
Пример:
Вычислить значение выражения 2(3x + 4) + 5(3x +4).
- Раскрываем скобки: 2*3x + 2*4 + 5*3x + 5*4
- Сокращаем одинаковые скобки: (2*3 + 5*3)x + 2*4 + 5*4
- Выполняем арифметические операции: 21x + 2*4 + 5*4
- Получаем ответ: 21x + 8 + 20 = 21x + 28
Таким образом, мы смогли сократить одинаковые скобки в выражении и получить упрощенный вид.
Раскрытие скобок
Прямые скобки в математике используются для обозначения группировки элементов. Это позволяет задавать порядок выполнения арифметических действий в математических выражениях. Раскрытие скобок – одна из основных операций при работе с алгебраическими выражениями.
Все элементы, находящиеся внутри скобок, считаются одним целым и должны быть умножены на коэффициент перед скобками. Для раскрытия скобок нужно умножить элементы внутри скобок на коэффициент, стоящий перед скобками.
Если внутри скобок стоит знак “-“, то знак умножения на коэффициент меняется на “-“, а все элементы внутри скобок умножаются на -1. Если внутри скобок есть другие скобки, то сперва нужно раскрыть их, начиная со внутренних скобок и двигаясь к внешним.
Пример: дано выражение 2(3x-1), нужно раскрыть скобки. Коэффициент перед скобками равен 2, поэтому нужно умножить каждый элемент внутри скобок на 2. Получаем: 2 * 3x – 2 * 1 = 6x – 2.
Важно помнить, что раскрытие скобок является обратной операцией к группировке элементов в скобки. Если требуется выполнить какую-то операцию внутри скобок, то необходимо сначала раскрыть скобки, а затем выполнить необходимую операцию.
Примеры задач с прямыми скобками
Пример 1:
Вычисли значение выражения: [7 + (14 – 9)] / 2
Решение:
1. Раскрываем скобки внутри: [7 + 5] / 2
2. Складываем числа внутри квадратных скобок: 12 / 2
3. Делим 12 на 2: 6
Ответ: 6
Пример 2:
Найди значение x в уравнении: [8 + (4 – x)] = 9
Решение:
1. Раскрываем скобки внутри: [8 + 4 – x] = 9
2. Складываем числа внутри квадратных скобок: 12 – x = 9
3. Вычитаем 12 из обеих частей уравнения: -x = -3
4. Делим обе части уравнения на -1: x = 3
Ответ: x = 3
Пример 3:
Вычисли значение выражения: [(7 + 3) / 2] * 4
Решение:
1. Складываем числа внутри круглых скобок: [10 / 2] * 4
2. Делим 10 на 2: 5 * 4
3. Умножаем 5 на 4: 20
Ответ: 20
Пример 4:
Решите уравнение: 2x + [3x – (5 – x)] = 28
Решение:
1. Раскрываем скобки внутри: 2x + [3x – 5 + x] = 28
2. Складываем числа внутри квадратных скобок: 6x – 5 = 28
3. Прибавляем 5 к обеим частям уравнения: 6x = 33
4. Делим обе части уравнения на 6: x = 5.5
Ответ: x = 5.5
Изучение скобок на примерах
Учебный курс математики в 6 классе включает в себя изучение простых арифметических действий со скобками. Скобки используются для обозначения приоритета операций и для группировки элементов выражений. Основные виды скобок – круглые, квадратные и фигурные.
Круглые скобки: используются для сгруппировки операций, определяя порядок их выполнения. Например:
ВыражениеРешение
| 3 + 4 * 2 | 11 |
| (3 + 4) * 2 | 14 |
| (6 – 2) * (5 + 3) | 32 |
Квадратные скобки: используются в матричных выражениях. Например:
- [3 2][4 1] = 3*4 + 2*1 = 14
- [1 2 3][3 4 5][5 6 7] = 1*4*7 + 2*5*5 + 3*6*3 = 94
Фигурные скобки: используются для обозначения множеств. Например:
- A = {1, 2, 3, 4, 5}
- B = {x | x ∈ N, x < 7}
Важно помнить, что скобки могут менять значение выражений, поэтому необходимо правильно использовать их в задачах.
Упражнения для закрепления материала
1. Вычислите значения выражений:
- [7 + (2 – 3)] + 4;
- 2 + (3 x 4) – [ 5 – (6 : 2)];
- (6 – 2) x (5 – 3) + 10.
2. Даны значения переменных:
| a | b | c |
| 5 | 2 | 7 |
Вычислите значения следующих выражений:
- a x b – [a – (b + c)];
- [(a – b) x (c + b)] : c;
- (a : b) + (c : a) – (b : c).
3. Определите, является ли результатом выражения число 10:
- [ (2 + 3) x 4 ] : 5 ;
- 8 – 5 + 7 – 5 ;
- (15 – 3) : 4 + 6 .
4. Решите уравнения:
- a + 2 = 7 ;
- 5b – 3 = 12 ;
- 4c + 1 = 2c – 5 .
5. Проверьте свои знания:
- Что обозначают прямые скобки [] в математике?
- Какие действия выполняются в выражении (5 + 2) х 3?
- Какую переменную необходимо найти, если уравнение выглядит следующим образом: 8 – x = 2?
Решение задач на применение скобок

В математике прямые скобки используются для группировки выражений и изменения приоритетов операций. Рассмотрим несколько задач, где нужно применять скобки:
- Задача 1. Вычислить значение выражения 3 + 5 × 4.
Если выполнить операции по очереди, то получится 23. Однако, если поставить скобки вокруг выражения 5 × 4, то получится (3 + 5) × 4 = 32.
- Задача 2. Вычислить значение выражения 25 ÷ 5 + 3 × 2.
Если выполнить операции по очереди, то получится 17. Однако, если поставить скобки вокруг выражений 25 ÷ 5 и 3 × 2, то получится (25 ÷ 5) + (3 × 2) = 17.
- Задача 3. Вычислить значение выражения 2 + 4 × 32.
Если выполнить операции по очереди, то получится 38. Однако, если поставить скобки вокруг выражения 32, то получится 2 + 4 × (32) = 38.
Таким образом, применение скобок позволяет корректно выполнить операции и получить правильный результат.
Видео по теме:
Вопрос-ответ:
Какие возможности дает использование прямых скобок в математике?
Прямые скобки в математике используются для обозначения множества, вектора, индекса, промежутка значений функции и для других целей.
Можно ли использовать круглые скобки вместо прямых в некоторых случаях?
В некоторых случаях, например, при обозначении элементов массива, можно использовать круглые скобки, но это зависит от контекста задачи и правил преподавателя.
Можно ли использовать прямые скобки для обозначения интервала?
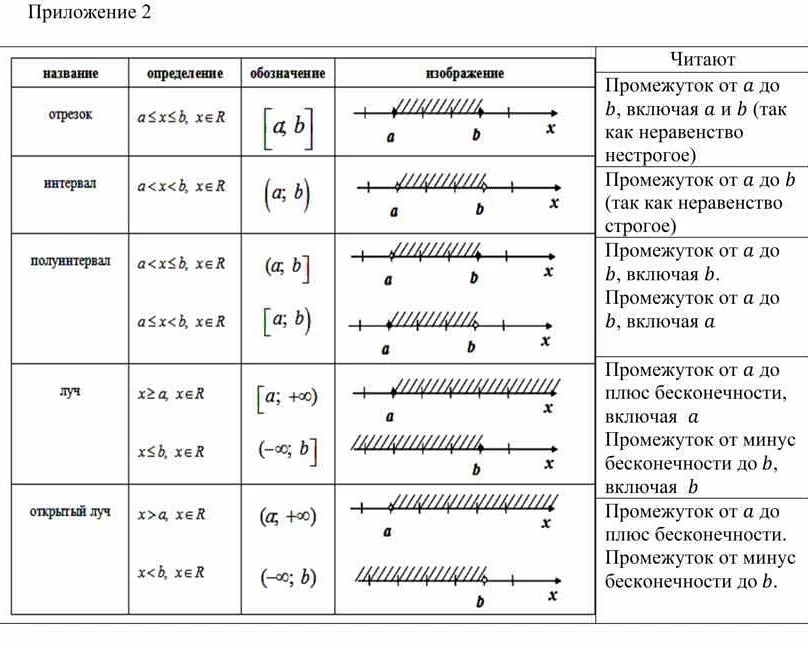
Для обозначения интервала промежутка использование прямых скобок неверно, используются круглые или квадратные скобки, например: (a, b) – открытый интервал, [a, b] – закрытый интервал или [a, b) и (a, b].
Могут ли прямые скобки использоваться для записи операций?
Прямые скобки не используются для записи операций, они обозначают некоторые значения (как, например, векторное произведение).
Какие математические функции используют прямые скобки?
Прямые скобки используют в математических функциях для обозначения элементов множества, например, A = {1, 2, 3} и B = {x | x > 0}.
Какие символы могут находиться внутри прямых скобок?
Внутри прямых скобок могут находиться любые символы (буквы, цифры, знаки пунктуации), которые необходимы для обозначения элементов множества.
Могут ли прямые скобки использоваться для обозначения векторов?
Да, обозначение вектора с помощью прямых скобок является одним из стандартных способов записи вектора, например, вектор a задается как a = [a1, a2, …, an].
Практическое применение прямых скобок
Прямые скобки в математике используются для группировки операций и элементов в выражениях. Вот несколько примеров их практического применения:
- Множества: прямые скобки могут использоваться для обозначения множества элементов. Например, множество всех целых чисел от 1 до 10 можно записать как {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}.
- Массивы: в программировании прямые скобки используются для доступа к элементам массива. Например, если у нас есть массив чисел arr = [1, 2, 3, 4], чтобы получить доступ к элементу с индексом 2, мы можем написать arr[2].
- Функции: в математике и программировании функции могут принимать аргументы в скобках. Например, функция получения квадратного корня в языке программирования Python может быть вызвана как math.sqrt(25), где 25 – аргумент функции, передаваемый в скобках.
Во всех этих случаях прямые скобки помогают явно идентифицировать группы элементов и аргументов, что облегчает их использование и понимание.
Выводы
Прямые скобки в математике обозначают группировку операций и указание порядка их выполнения. Если в выражении есть скобки, то сначала выполняются операции внутри скобок, а затем остальные операции.
При использовании прямых скобок важно следить за их корректностью и правильной установкой. Неправильно расставленные скобки могут привести к ошибкам в вычислениях и некорректным результатам.
Помимо прямых скобок в математике существуют еще и круглые, фигурные, и квадратные скобки. Они также используются для группировки операций и задания приоритета выполнения действий.
Знание правильного использования скобок является важной базовой навыком для успешного изучения математики и решения задач.
- Прямые скобки используются для группировки операций.
- При использовании скобок важно следить за их правильной установкой.
- Круглые, фигурные, и квадратные скобки также используются в математике для группировки операций.
- Знание правильного использования скобок является важным навыком для решения задач.






