2 3 части в математике – это основной элемент работы с дробями. Это дробь, которую можно записать в виде 2/3, что означает, что мы имеем две трети целого числа. Понимание работы с дробями является важным в математике и нужно для дальнейшего изучения алгебры и геометрии.
В математике вы имеете дело с множеством понятий и терминов, которые могут быть конфузными при первом прочтении. Один из таких терминов – 2/3 части, который используется в различных контекстах, таких как дроби, проценты, пропорции и т.д. В этой статье мы рассмотрим, что означает 2/3 часть и как его использовать в математических вычислениях.
2/3 часть – это дробь, где числитель равен двум, а знаменатель равен трем. Она представляет собой долю, равную двум из трех равных частей. Другими словами, если вы разделите что-то на три равные части, то 2/3 часть будет составлять две из этих трех частей.
2/3 также может быть записано в процентном виде или в виде десятичной дроби. Например, 2/3 можно перевести в проценты, умножив его на 100. В этом случае 2/3 будет равен 66,67%. Он также может быть записан в виде десятичной дроби, где 2/3 равен 0,6667 или 0,67 (округляется до двух знаков после запятой).
3 части в математике: понятие и определение
3 части в математике – это одна из основных методик решения математических задач, которая предусматривает разделение всех элементов математического выражения на три основные части: первичное число, знак операции и вторичное число. Эта методика гарантирует правильное выполнение математических вычислений и упрощения задач.
Первичное число представляет собой первую часть любого математического выражения. Это может быть любое число или выражение, которое стоит перед знаком операции. Например, в выражении 2 + 3, первичным числом является число 2.
Знак операции – это символ, который указывает, какое действие должно быть выполнено с первичным числом и вторичным числом. Это может быть знак плюс, минус, умножить или разделить. Например, в выражении 2 + 3, знак операции является знаком плюс.
Вторичное число – это вторая часть любого математического выражения. Она может быть любым числом или выражением, которое следует за знаком операции. Например, в выражении 2 + 3, вторичным числом является число 3.
Применение 3 частей в математике упрощает сложные математические вычисления и снижает вероятность возникновения ошибок в процессе решения задач. Чтобы правильно использовать эту методику, необходимо понимать, что каждое математическое выражение может быть разбито на три части и какие действия могут быть выполнены с использованием знаков операции.
Видео по теме:
Основы понятия двух и трех частей в математике

Понятие двух и трех частей являются фундаментальными в математике. Они используются для описания и классификации объектов или явлений, которые можно поделить на две или три неодинаковые части.
Примерами могут служить геометрические фигуры, которые можно разделить на две или три части, используя линии или поверхности разлома. Например, треугольник можно разделить на две части, соединив середины двух сторон. Это относится к понятию двух частей.
Трех частей можно найти в задачах, связанных с вероятностью. Например, для выражения вероятности события, которое может произойти с равной вероятностью, необходимо разделить все возможные исходы на три части. Например, можно рассмотреть выбор одной из трех разных цветов маркера из коробки, которая содержит красные, синие и зеленые маркеры.
Понимание двух и трех частей является важным компонентом многих областей математики, начиная с геометрии и заканчивая вероятностью. Эти концепции могут быть применены как в теоретических, так и в практических задачах. Они могут быть использованы для решения проблем и упрощения сложных задач, которые могут появиться в различных областях деятельности.
Основные понятия и термины в математике
Математика – это наука, которая изучает количество, структуру, пространство и изменение.
Число – это математический объект, который используется для измерения количества или размерности.
Операция – это математическое действие, которое выполняется над числами или другими математическими объектами.
Функция – это математический объект, который связывает каждый элемент из одного множества с элементами другого множества.
Геометрия – это наука, которая изучает пространственные формы, размеры и их связи.
Треугольник – это геометрическая фигура, которая состоит из трех линий, называемых сторонами, и трех углов между сторонами.
Дробь – это число, которое представлено как отношение одного целого числа к другому.
Пропорция – это соотношение двух дробей или отношение двух отрезков.
- Декартова система координат – это способ представления точек на плоскости или в пространстве с помощью координат.
- Уравнение – это математическое выражение, которое утверждает равенство двух выражений.
- Интеграл – это математический объект, который используется для нахождения площади под кривой на графике.
Вектор – это математический объект, который имеет направление и длину и может использоваться для представления движения или силы.
Матрица – это таблица чисел или символов, которая используется для представления линейных уравнений и преобразований.
ТерминОписание
| Логарифм | Метод для измерения количества, используемый для решения уравнений. |
| Производная | Мера изменения функции по отношению к изменению ее аргумента. |
| Измерение | Процесс оценки размера, количества и веса объекта. |
Условия и правила для определения двух и трех частей
Две части – это деление объекта, числа, предложения или иной структуры на две равные части. Для определения двух частей нужно выполнить следующие условия:
- Объект должен быть делится на две равные части.
- Обе части должны быть одинаковыми по структуре, размеру и содержанию.
- Обе части должны быть разделены знаком, который показывает равномерное разделение.
Три части – это деление объекта на три равные части. Для определения трех частей необходимо выполнить следующее условие:
- Объект должен быть разделен на три равные части.
- Обе части должны быть одинаковыми по структуре, размеру и содержанию.
Правила можно использовать для множества задач в математике, литературе и других науках. Выполнение этих условий позволяет точно разделить объект на нужное количество частей и провести анализ каждой из них. Также, знание этих правил может помочь в повседневной жизни в области экономики, бизнеса и других сферах.
Случаи расчета двух и трех частей в математике
Расчет двух и трех частей появляется в математике в различных контекстах и задачах. В общем, двух и трех частей можно понимать как разбиение некоторого целого числа на две или три равные (или не равные) части.
Один из самых распространенных случаев расчета двух и трех частей связан с долями и процентами. Например, если вас просят поделить некоторую сумму денег на две или три части в соответствии с заданными процентными долями каждой части, вы можете использовать формулы пропорций или просто найти соответствующее значение для каждой части.
Другой случай, когда возникает расчет двух и трех частей, связан с геометрией и разбиением фигур на части. Например, при разбиении прямоугольника на две или три части можно использовать геометрические пропорции или формулы площади, чтобы найти размеры каждой части.
Расчет двух и трех частей также может появляться в задачах, связанных с вероятностным распределением. Например, если вас просят разбить некоторую выборку на две или три части в соответствии с заданными вероятностными долями каждой части, вам нужно будет использовать формулы вероятности или другие методы статистического анализа.
В целом, расчет двух и трех частей может быть полезным для решения различных задач в математике и других областях знания. Но в каждом конкретном случае необходимо выбирать подходящий метод и формулы в соответствии с заданными условиями и требованиями.
Практические примеры двух и трех частей в математике
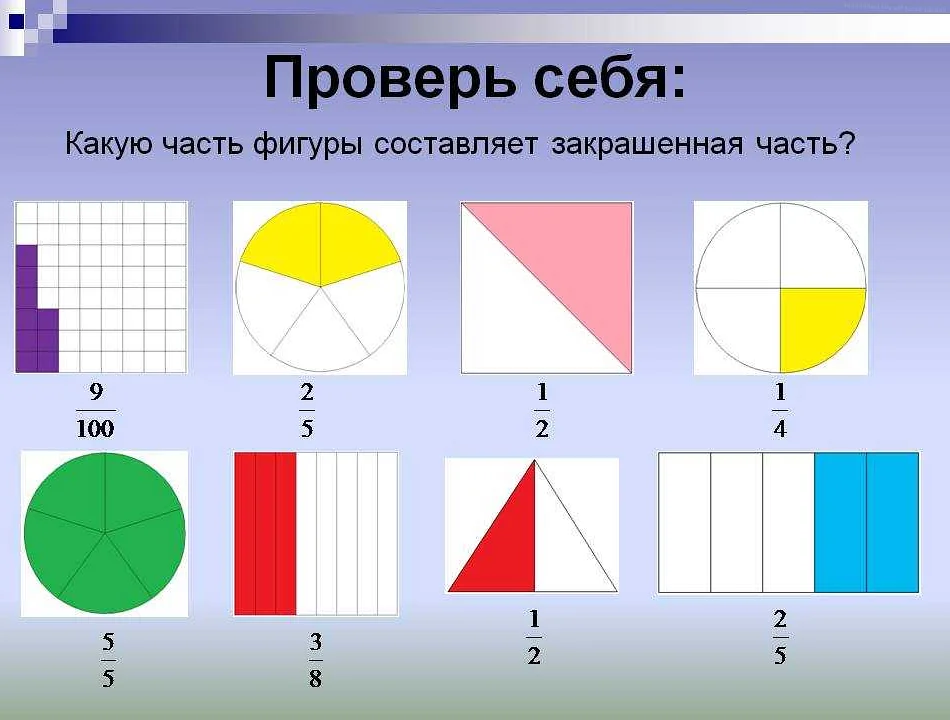
Концепция двух и трех частей находит применение в различных областях математики, физики, химии и даже экономике. В математике, эти концепции рассматриваются как методы решения уравнений.
Для примера, уравнение 2x + 5 = 11 может быть решено с использованием двух частей: сначала мы отнимаем 5 от обеих сторон уравнения, чтобы получить 2x = 6, а затем делим обе стороны на 2, чтобы выразить x: x = 3.
В качестве другого примера уравнение более высокой степени, такое как x^2 + 5x + 6 = 0, может быть решено с использованием трех частей. Сначала мы находим два числа, которые в сумме дают 5 и произведение которых равно 6. В данном случае это 2 и 3. Затем мы разбиваем x^2 + 5x + 6 на два меньших уравнения: x^2 + 2x + 3x + 6 = 0. Далее приравниваем каждое из них к нулю. Полученные уравнения x^2 + 2x + 3 = 0 и x + 2 = 0 решаем методом двух частей, выражая x.
- В физике, пример двух частей может быть использован при расчете скорости движения: скорость = расстояние / время.
- В химии, применение двух и трех частей может быть использовано при расчете процентного соотношения реакционных веществ.
- В экономике, примером использования концепции трех частей может стать расчет процентной ставки и суммы процентов в банке.
Все эти примеры демонстрируют широкое применение концепции двух и трех частей в математике и других науках.
Преимущества и применение двух и трех частей в математике
Две и три части являются важными понятиями в математике, которые находят широкое применение в решении различных задач. Например, две части могут обозначать долю или процент от целого, а три части использовать при вычислении вероятности.
Преимущества использования двух частей:
- Легкость интерпретации
- Простота в вычислении
- Широкое применение в повседневной жизни
Преимущества использования трех частей:
- Позволяет более точно вычислять вероятность
- Применяется в статистике и экономике
- Понятен даже для людей без специальной математической подготовки
Использование двух и трех частей помогает упрощать решение задач и делать их более доступными для понимания. Кроме того, эти понятия находят широкое применение в повседневной жизни и различных научных областях.
Роль двух и трех частей в решении задач и уравнений
Две и три части часто встречаются в математических уравнениях и задачах. Они играют важную роль в решении уравнений и задач, особенно в алгебре и геометрии.
Две части можно найти в уравнениях типа “a+b=c”. В таких уравнениях необходимо найти значение неизвестной переменной, которая может находиться как в левой, так и в правой части уравнения. Для решения уравнения необходимо перенести один из слагаемых в другую часть уравнения и затем разделить обе стороны на коэффициент перед неизвестной переменной.
Три части могут использоваться в геометрии, например, для вычисления площади треугольника. Знание трех сторон треугольника позволяет вычислить его площадь по формуле Герона. Для этого необходимо сначала вычислить полупериметр треугольника, который равен сумме всех сторон, разделенной на два. Затем площадь вычисляется по формуле, которая содержит полупериметр и длины сторон.
В целом, знание двух и трех частей может быть полезным при решении математических задач и уравнений. Решение уравнений и задач требует точности и полного понимания задачи, а знание двух и трех частей может помочь упростить подход к решению и повысить точность.
Особенности вычисления двух и трех частей в математике
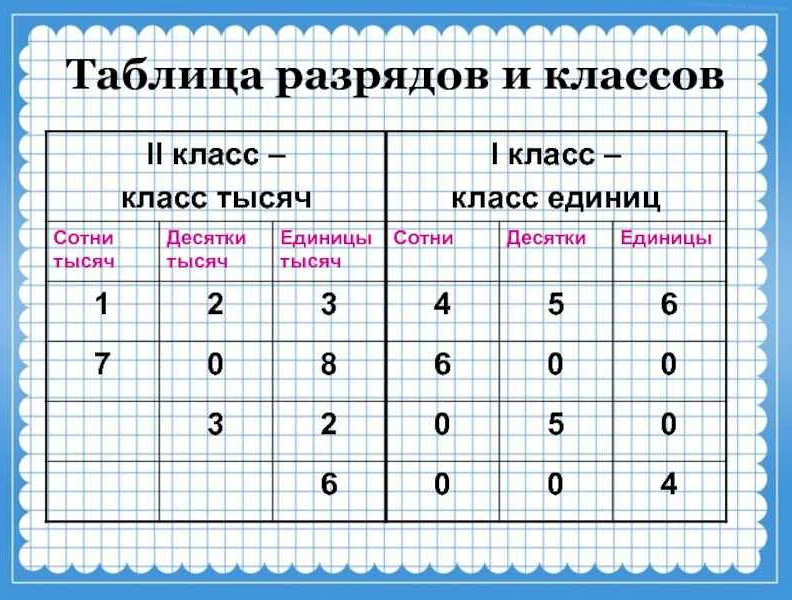
Две части в математике часто используются для вычисления процентов и долей. Например, если нужно найти 20% от числа, необходимо умножить это число на 0,2 (что составляет 1/5 числа). Для вычисления доли, например 3/5 от числа, необходимо умножить это число на 0,6 (что равно 60%). Важно помнить, что вычисления с двумя частями могут быть выполнены при помощи умножения и деления на простые числа.
Три части в математике находят свое применение, например, при вычислении процента изменения. Если произошло увеличение числа на 10%, то новое число будет составлять 110% от исходного. Для вычисления процентного изменения, нужно вычислить разность между конечным и исходным значением, поделить эту разность на исходное значение и умножить на 100. Кроме того, три части могут использоваться для вычисления вероятности. В этом случае, необходимо разделить количество возможных исходов на общее количество исходов.
- При вычислении двух частей, необходимо учесть все значения, которые могут повлиять на результат.
- При вычислении трех частей, необходимо учитывать все возможные варианты исходов.
Важно помнить, что вычисления с двумя и тремя частями могут быть использованы в различных областях науки и техники, а также в повседневной жизни.
Различия и сходства двух и трех частей в математике
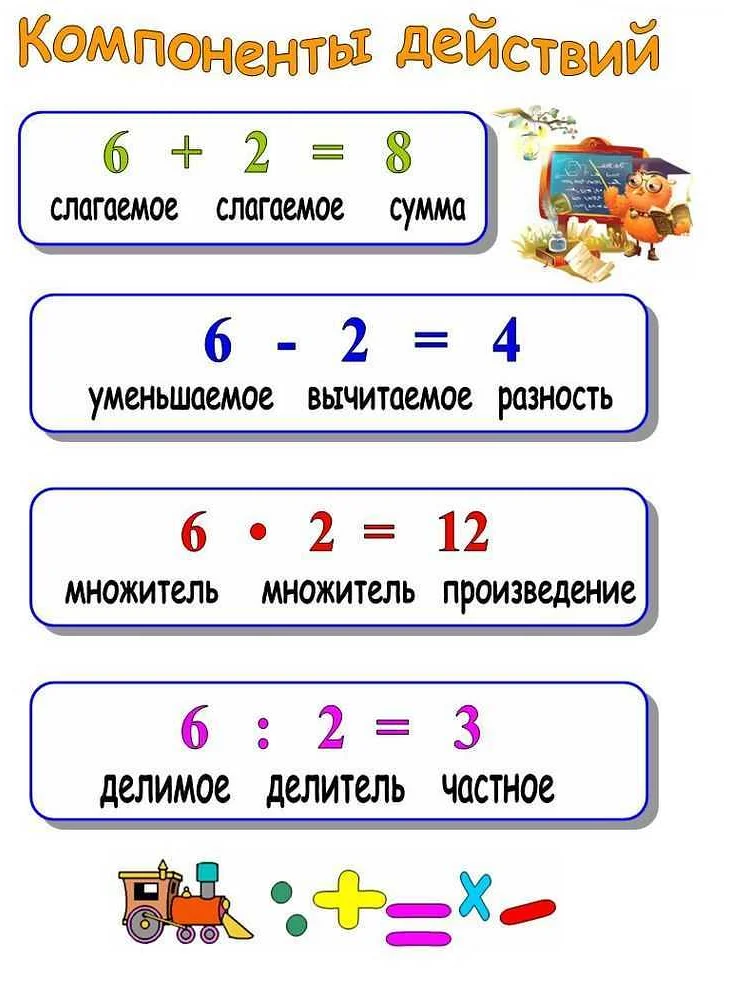
В математике понятие “2 3 части” относится к пропорциональным отношениям и частям целого. В обоих случаях необходимо иметь представление о соотношении разных частей.
Различие между двумя частями и тремя частями заключается в количестве частей, которые нужно разделить на равные доли. В случае двух частей, представимых в виде дроби, одна часть будет числителем, а другая — знаменателем. В пропорции, описывающей отношение двух частей, одна часть будет занимать первое место, а другая — второе. В случае трех частей необходимо разделить предмет на три равные доли и определить соотношение каждой из этих частей относительно целого.
Однако, как и в случае с двумя частями, в трех частях необходимо иметь представление о соотношении разных частей в целом. В числовых пропорциях нужно понимать, как соотносятся две из трех частей в том случае, если известно соотношение третьей. В геометрии, например, необходимо понимать, как соотносятся процентные доли разного цвета относительно всей поверхности.
В целом, различия между двумя частями и тремя частями связаны с количеством частей, которые нужно определить в пропорции или отношении. Однако в обоих случаях необходимо иметь представление о соотношении разных частей в целом.
Влияние двух и трех частей на последующие вычисления
В математике понятие “2 3 части” применяется, когда нужно разделить целое число или величину на равные части. Например, если нужно разделить отрезок длиной 6 метров на 2 равные части, каждая часть будет равна 3 метрам. Если разделить его на 3 равные части, каждая будет равна 2 метрам.
Разделение на две или три части может оказать значительное влияние на последующие вычисления. В частности, при расчетах с долями, дробями или процентами, знание того, на сколько частей разбито целое число или величина, может быть очень важным.
Например, если имеется отрезок длиной 9 метров, и его нужно разделить на 2 части равной длины, каждая часть будет составлять 4,5 метра. Если задача состоит в том, чтобы найти длину одной из этих частей, в формулах нужно использовать дробь 1/2, чтобы обозначить долю отрезка. Тогда формула для нахождения длины одной части будет выглядеть так: 9 м * 1/2 = 4,5 м.
Если бы отрезок был разделен на 3 равные части, каждая часть была бы длиной 3 м. В этом случае, при нахождении длины одной части, нужно было бы использовать дробь 1/3. Формула для нахождения длины одной части выглядела бы так: 9 м * 1/3 = 3 м.
Поэтому, важно понимать, на сколько частей разбито целое число или величина, при выполнении математических операций. Это помогает правильно задавать формулы и получать необходимые результаты.
Значимость знания двух и трех частей в математике для повседневной жизни
Математика является одним из самых важных предметов в нашей жизни. Знание двух и трех частей в математике помогает нам понимать мир вокруг нас, рассчитывать расходы, прогнозировать результаты и многое другое.
Рассчеты в финансовой и бизнес-сферах
В современном мире наши финансовые решения зависят от математических вычислений. При покупке товаров и услуг мы должны рассчитывать стоимость и оценивать свои расходы. Если вы владеете знанием двух и трех частей в математике, то сможете быстрее и точнее рассчитать сумму, которую вы потратите.
Практическое применение математики в жизни
Кроме финансов, математика помогает нам решать множество повседневных задач. Например, знание процентов и долей может помочь вам рассчитать пропорции ингредиентов для приготовления блюда.
- Кроме того, знание двух и трех частей позволяет рассчитывать время, необходимое для выполнения задач и выработки навыков продуктивности.
- Знание геометрических форм может быть полезным при решении ежедневных задач, таких как перестановка мебели или монтаж рамок.
- Понимание математических принципов также может помочь вам в развитии логического мышления и принятии обоснованных решений.
Кратко говоря, знание двух и трех частей в математике необходимо для повседневной жизни. Эти знания помогают нам в финансах, бизнесе и многих других областях.
Вопрос-ответ:
Как определить, что две дроби эквивалентны?
Две дроби a/b и c/d эквивалентны, если a*d = b*c. Например, дроби 2/3 и 4/6 эквивалентны, так как 2 * 6 = 3 * 4.
Как сократить дробь?
Для того чтобы сократить дробь a/b, нужно найти такую общую делимость a и b и поделить их на нее. Например, дробь 6/9 можно сократить до 2/3, разделив числитель и знаменатель на 3.
Что такое десятичная дробь?
Десятичная дробь – это дробь вида a/10^b, где a и b – целые числа. Например, дробь 3/1000 – это десятичная дробь, так как ее можно записать как 0,003.
Как перевести десятичную дробь в обыкновенную?
Для перевода десятичной дроби в обыкновенную нужно записать дробь так, чтобы знаменатель был степенью 10. Например, десятичную дробь 0,25 можно записать как 25/100, а затем сократить до 1/4.
Как сложить две дроби?
Для сложения двух дробей нужно привести их к общему знаменателю, затем сложить числители и записать результат в виде несократимой дроби. Например, чтобы сложить 1/3 и 2/5, нужно привести дроби к общему знаменателю 15: 1/3 = 5/15, 2/5 = 6/15. Затем суммируем числители: 5/15 + 6/15 = 11/15.
Как умножить две дроби?
Для умножения двух дробей нужно умножить числитель первой дроби на числитель второй дроби и знаменатель первой дроби на знаменатель второй дроби, затем записать результат в виде несократимой дроби. Например, чтобы умножить 2/3 на 4/5, нужно выполнять следующие действия: 2/3 * 4/5 = (2 * 4)/(3 * 5) = 8/15.
Что такое дроби с отрицательным знаменателем?
Дробь с отрицательным знаменателем – это дробь, у которой знак числителя и знаменателя разные. Например, дробь -2/3. Такую дробь можно преобразовать к дроби с положительным знаменателем, поменяв знаки числителя и знаменателя местами: -2/3 = 2/-3.






