Что такое ch в математике? Это гиперболический косинус – функция, которая описывает гиперболическую тригонометрию, используемую в физике и инженерии. Узнайте, как расчитать ch и где он применяется.
ch – один из математических терминов, который часто используется в теории функций и математическом анализе. Выражение ch(x) обозначает гиперболический косинус(x), который является одной из функций гиперболических тригонометрии.
Гиперболический косинус является аналогом обычного косинуса, который используется в тригонометрии. Он определяется как:
ch(x) = (e^(x) + e^(-x)) / 2
При этом e – основание натурального логарифма, равное примерно 2,71828.
Гиперболический косинус имеет свои собственные свойства и формулы, которые позволяют решать различные задачи в математическом анализе, дифференциальных уравнениях и других областях математики.
Определение ch
ch – это функция гиперболического косинуса, которая используется в математике для решения уравнений и вычисления различных значений. Эта функция является одной из шести гиперболических тригонометрических функций, которые имеют аналоги в обычных тригонометрических функциях.
ch(x) можно выразить через экспоненту: ch(x) = (ex + e-x)/2. Таким образом, ch(x) равняется сумме экспоненты x и экспоненты минус x, поделенных на 2.
Функция ch(x) является четной функцией. Это означает, что ch(-x) = ch(x) и график функции симметричен относительно оси Y.
Функция гиперболического косинуса также связана с гиперболическими синусом и тангенсом, и может быть выражена через них. Для примера: ch(x) = cosh(x) = (ex – e-x)/2.
Формула ch
Формула ch, где ch – гиперболический косинус, представляет собой математическое выражение, где ch(x) = (e^x + e^(-x))/2
Гиперболический косинус является одной из гиперболических тригонометрических функций, которые аналогичны обычным тригонометрическим функциям (синус, косинус), но используют гиперболические функции вместо тригонометрических.
Формула ch может быть использована для решения различных задач в математике, физике и инженерных науках. Например, она может быть применена при изучении колебаний, электромагнетизма и теплопроводности.
С помощью формулы ch можно также определить производную и интеграл гиперболического косинуса, что также имеет важное значение в решении многих задач.
Обратная функция ch(x) – это аркгиперболический косинус (arccosh(x)), который также используется в математике и науке.
График функции ch
Функция гиперболического косинуса (ch) – это одна из шести гиперболических тригонометрических функций. Она имеет такую же формулу, как и косинус, но работает с гиперболическими аргументами. Посмотрим, как выглядит график функции ch.
График функции ch имеет форму чашки и напоминает параболу, но его концы не сходятся на бесконечности, а на конечном числе. Ось симметрии графика является осью OY. Функция ch является четной и монотонно возрастающей. Ее значения растут от бесконечной нижней границы.
Пересечения графика с осью OX происходят в точках х = 0 и х = ±iπ. Также график имеет асимптоту y = 1, которую он никогда не достигает. Это связано с тем, что гиперболический косинус имеет бесконечную производную в этой точке.
- При x = 0 значение функции ch равно 1, так как ch(0) = cosh(0) = (e^0 + e^0)/2 = 1.
- При x = 1, значение функции равно примерно 1,54.
- При x = 2, значение функции равно примерно 3,63.
График функции ch играет важную роль в математике и физике. Он используется для моделирования кривых форм, таких как арки мостов и крыш столбов. Также он используется при решении задач теории поля в физике высоких энергий.
Свойства функции ch
Функция гиперболического косинуса ch является одной из шести тригонометрических функций гиперболического класса. Её определение основано на экспоненциальной функции, а именно, ch(x) = (e^x + e^(-x))/2.
Свойства функции ch:
- ch(0) = 1. Действительно, при x=0 имеем (e^0 + e^(-0))/2 = (1+1)/2 = 1.
- ch(-x) = ch(x). Функция ch симметрична относительно оси Oy.
- ch(x) > 0 для любого x. Функция ch всюду положительна.
- Она обладает свойством линейности: ch(ax + b) = a * ch(x) + b, где a, b – константы.
- Также выполнено свойство ch^2(x) – sh^2(x) = 1.
Эти свойства позволяют использовать функцию гиперболического косинуса в решении различных задач, включая задачи математической физики, статистики, механики и др.
Интеграл функции ch

Интеграл функции ch – это интеграл от экспоненты, где в качестве аргумента выступает гиперболический косинус. Для определения интеграла функции ch необходимо применить метод интегрирования по частям, а именно:
- Подставить гиперболический косинус вместо переменной в интеграл;
- Взять производную от гиперболического косинуса;
- Интегрировать полученное выражение.
Таким образом, интеграл функции ch сводится к интегрированию произведения функций с использованием метода интегрирования по частям.
Применение интеграла функции ch широко используется в математике, физике, технике и других науках. Например, он применяется при решении задач теплопроводности, при расчете электрических цепей и др.
Интеграл функции ch также используется при построении графиков гиперболических функций, а также для обобщения понятия синуса и косинуса на гиперболические функции.
Производная функции ch

Гиперболические функции – это функции, которые стоят в числителе или знаменателе гиперболических тригонометрических функций. Одной из таких функций является функция ch(x). Её график представляет собой параболу, которая отражена относительно оси Ох.
Чтобы вывести производную этой функции, необходимо использовать определение производной. Производная функции ch(x) выражается формулой:
ch'(x) = sh(x)
sh(x) – это гиперболический синус, который определяется формулой:
sh(x) = (ex – e-x)/2
Используя производную функции sh(x), можно вывести производную функции ch(x). Таким образом, производная функции ch(x) равна гиперболическому синусу от аргумента функции.
Используя производную функции ch(x), можно вывести также вторую производную функции ch(x). Она выражается формулой:
ch”(x) = sh'(x) = ch(x)
Таким образом, вторая производная функции ch(x) равна самой функции ch(x).
Примеры решения задач с использованием функции ch
Пример 1: Найдите значения функции y = ch(x) при x = 0, x = 1 и x = -1.
Решение:
- При x = 0, ch(x) = ch(0) = 1
- При x = 1, ch(x) = ch(1) ≈ 1.543
- При x = -1, ch(x) = ch(-1) ≈ 1.543
Пример 2: Решите уравнение ch(x) = 3.
Решение:
- ch(x) = 3
- e^x + e^(-x) = 6
- Положим e^x = t, тогда e^(-x) = 1/t
- t + 1/t = 6, умножаем на t: t^2 + 1 = 6t
- t^2 – 6t + 1 = 0
- t1 = 3 + 2√2, t2 = 3 – 2√2
- e^x = 3 + 2√2, e^(-x) = 1/(3 + 2√2)
- x ≈ 1.316, x ≈ -1.316
Пример 3: Найдите производные функции y = ch(x) и y = sh(x).
Решение:
- y’ = ch'(x) = sh(x)
- y” = ch”(x) = ch(x)
- y’ = sh'(x) = ch(x)
- y” = sh”(x) = sh(x)
Практическое применение функции ch в математике и физике
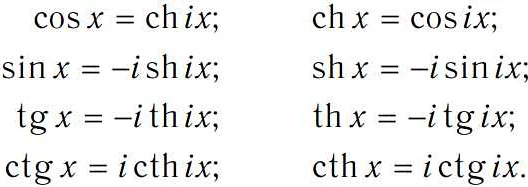
Функция гиперболического косинуса, ch(x), играет важную роль в математике и физике. Она определяется как:
ch(x) = (exp(x) + exp(-x))/2
где exp(x) – экспонента, то есть e в степени x. Эта функция используется в решении уравнений и представлении синусов и косинусов через гиперболические функции.
В математическом анализе ch(x) используется в качестве примера функции, которая непрерывна и дифференцируема. Она также является частью формулы Эйлера:
e^(ix) = cos(x) + i * sin(x) = ch(i*x) + i * sh(i*x)
- где i – мнимая единица, то есть i² = -1;
- cos(x) и sin(x) – косинус и синус соответственно.
В физике функция ch(x) используется в решении различных задач, связанных с движением. Например, она используется в уравнении движения грузовика на гору:
m * a = F – m * g * sin(theta) – k * ch(v)
- где m – масса грузовика;
- a – ускорение грузовика;
- F – сила, толкающая грузовик вперед;
- g – ускорение свободного падения;
- theta – угол, под которым поднимается грузовик;
- v – скорость грузовика;
- k – коэффициент сопротивления дороги.
Из этого уравнения можно определить, как изменится скорость грузовика в зависимости от различных факторов, таких как его масса, сила тяги, уклон дороги и т.д.
Отличия функции ch от других функций тригонометрии и гиперболических функций
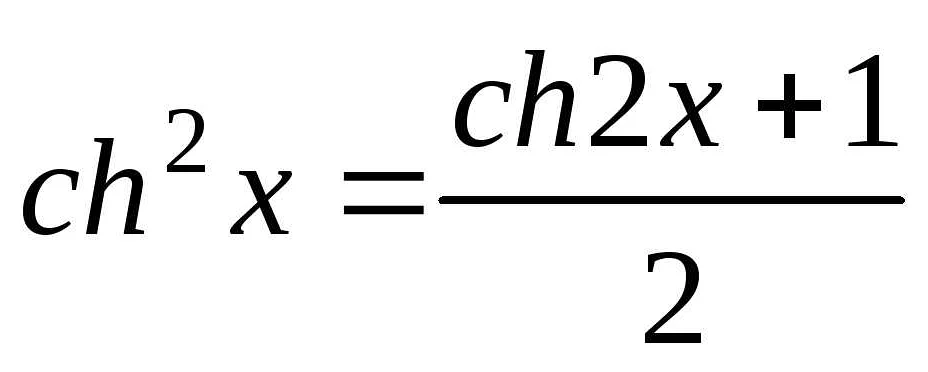
Функция ch является гиперболической функцией. В отличие от тригонометрических функций, которые описывают соотношения между сторонами прямоугольного треугольника, гиперболические функции описывают гиперболы. Функция ch описывает гиперболический косинус, который определяется как отношение стороны прямоугольного гиперболического треугольника к его гипотенузе.
Гиперболические функции отличаются от тригонометрических функций тем, что они не являются периодическими функциями. Тригонометрические функции описывают колебания, а гиперболические функции описывают рост и убывание. Функция ch не имеет периодических колебаний, она растет или убывает в зависимости от значения аргумента.
Некоторые гиперболические функции могут быть выражены через тригонометрические функции, но такое выражение не применимо к функции ch. Функция ch не может быть выражена как комбинация тригонометрических функций, поэтому она имеет свои уникальные свойства и применения в математике и физике.
Функция ch имеет множество практических применений в физике и технике. Она используется для описания волновых процессов в электромагнитной теории, связанных с электрическими полями и магнитными полями. Также функция ch играет важную роль в кинематике и динамике твердого тела и в теории возмущений в квантовой механике.
Дополнительные материалы по теме
Если вы хотите углубиться в тему “ch в математике”, рекомендуем изучить следующие материалы:
- Справочник математика: в разделе “Таблицы и формулы” вы найдете подробную информацию об использовании символа “ch” в математических выражениях.
- Учебники по математике: для углубленного изучения вопроса рекомендуется обратиться к учебникам по различным разделам математики, таким как алгебра или тригонометрия.
- Онлайн-курсы по математике: многие образовательные платформы, такие как Coursera или Udemy, предлагают онлайн-курсы по математике, которые могут помочь вам получить глубокие знания в этой области.
Не забывайте, что лучший способ научиться математике – это регулярные занятия и практика. Постепенно углубляйтесь в тему и применяйте полученные знания на практике, чтобы укрепить свои навыки в области математики.
Видео по теме:
Что такое ch в математике?
ch – это функция гиперболического косинуса, определяемая следующим образом: ch(x) = (e^x + e^(-x))/2
Как ch связано с другими гиперболическими функциями?
ch(x) связано с функциями sinh и cosh следующим образом: ch(x) = cosh(ix)
Где ch используется в математике?
Функция ch широко используется в теории вероятностей и математической физике, а также в других областях математики, включая дифференциальное и интегральное исчисление.
Какова производная функции ch?
Производная функции ch(x) равна $\frac{d}{dx}ch(x) = sinh(x)$.
Каков график функции ch?
График функции ch является параболой, проходящей через точку (0,1) и имеющей ось симметрии, параллельную оси x.
Как использовать функцию ch в программировании?
В большинстве языков программирования функция ch(x) реализована в стандартной математической библиотеке. Для подсчета значения ch(x) в программе требуется вызов соответствующей функции, например, ch(x) в Python реализуется как math.cosh(x).






