IJK в математике – это система координат, используемая для указания положения трехмерных объектов. Узнайте, как работает эта система и как ее применяют в практике математики и графики.
Математика – это не только числа и формулы, это также язык, на котором описываются законы природы и мир, в котором мы живем. Один из основных элементов этого языка – это символы, которые используются для обозначения математических объектов и операций. Один такой символ, часто появляющийся в математических выражениях, – это ijk.
Символ i обычно используется для обозначения мнимой единицы – числа, равного корню из -1. Символ j и символ k используются для обозначения векторов в трехмерном пространстве. Таким образом, выражение ijk может обозначать произведение мнимой единицы и двух ортогональных векторов, или же произведение трех векторов.
Некоторые из наиболее известных применений ijk в математике включают использование его в кватернионах, где i, j и k обычно используются для обозначения базисных векторов в трехмерном пространстве. А также в векторном бескоординатном формализме матриц, где i, j и k используются для обозначения векторов в трехмерном пространстве.
Определение ijk
ij – это матрицу, которая представляет собой произведение двух векторов i и j, где:
- i и j – это элементы векторного пространства;
- произведение i и j определяется через правило векторного произведения, которое описывает свойства двух векторов.
Таким образом, матрица ij является квадратной матрицей размерности 3х3.
k – это третий базисный вектор векторного пространства, который определяется через правило векторного произведения двух векторов i и j:
- k = i × j;
- знак × обозначает векторное произведение, которое определяется через правило правой руки – то есть когда правой рукой провести вектор i в сторону вектора j, то она переведется в направление вектора k.
Таким образом, вектор k перпендикулярен плоскости, образованной векторами i и j, и ортогонален им обоим.
Видео по теме:
Как использовать ijk в векторной алгебре
Векторы – это геометрические объекты, используемые в физике, математике и других научных областях. Они могут быть заданы как направленные отрезки, которые имеют длину и направление. Векторный анализ использует компоненты вектора для определения его длины, направления и других свойств.
Компоненты вектора могут быть представлены в форме ijk, где i, j и k – это единичные векторы в направлениях осей x, y и z соответственно. Использование i, j и k упрощает запись компонентов вектора и позволяет лучше понимать его свойства.
Например, если вектор имеет компоненты (3,4,-2), то он может быть записан в виде 3i + 4j – 2k. Это удобно для нахождения длины вектора, его направления и скалярного произведения с другими векторами.
Операции векторной алгебры, такие как сложение, вычитание и умножение на скаляр, также могут быть выполнены при помощи компонент ijk. Например, чтобы сложить два вектора, их компоненты i, j и k складываются по отдельности.
Таким образом, ijk представляют собой удобный способ представления компонент вектора в векторной алгебре. Они помогают упростить запись и выполнение операций, связанных с векторами, и позволяют лучше понимать их свойства.
ijk и крестовое произведение векторов
Крестовое произведение векторов – это операция, которая дает нам новый вектор, перпендикулярный двум начальным векторам. В математике используется сокращенная запись такой операции как ijk, где i, j и k – это базисные векторы в трехмерном пространстве.
При выполнении операции крестового произведения, мы сначала находим длины векторов в каждом измерении с помощью формулы:
a1b2 – a2b1
Затем мы упорядочиваем вычисленные значения в соответствии с порядком следования базисных векторов: i, j, k. Полученный вектор имеет координаты, соответствующие упорядоченным значениям, в порядке i, j, k.
Например, если у нас есть два вектора a = [1, 2, 3] и b = [4, 5, 6], то их крестовое произведение будет выглядеть следующим образом:
i
j
k
| a | 2×6 – 3×5 | 3×4 – 1×6 | 1×5 – 2×4 |
| b | |||
| a x b | -3 | 6 | -3 |
Таким образом, a x b = [-3, 6, -3]
Крестовое произведение векторов используется во многих областях науки и техники, включая физику, геометрию, компьютерную графику и многие другие.
ijk и смешанное произведение векторов
Векторное произведение двух векторов a и b дает новый вектор, перпендикулярный плоскости, образованной векторами a и b. Однако, когда имеется три вектора a, b и c, можно использовать смешанное произведение, чтобы найти объем тройки векторов, образованной ими.
Смешанное произведение векторов a, b и c выражается как ijk(a x b) · c, где i, j и k – оси координатных направлений. Результат смешанного произведения – скалярное значение, которое равно объему параллелепипеда, образованного векторами a, b и c. Если объем положителен, то вектор c находится по одну сторону плоскости, образованной векторами a и b, в то время как, если он отрицателен, то находится по другую сторону.
Смешанное произведение векторов может использоваться в различных областях математики, физики и геометрии. Например, его можно использовать для нахождения объема тетраэдра, образованного четырьмя векторами.
Интересный факт: ijk – это базисные компоненты трехмерного евклидова пространства, и они образуют систему координат. Поэтому, смешанное произведение векторов можно рассматривать как определитель матрицы 3 на 3, составленной из компонент указанных базисных векторов.
ijk и матрицы вращения

Одним из важных применений комплексных чисел в математике является задание движения в трехмерном пространстве. Для описания движения объекта или системы объектов в трехмерном пространстве используются матрицы вращения.
Существует несколько способов определения матриц вращения, но наиболее распространенный способ основан на использовании базиса ijk. Этот базис образуется в трехмерном пространстве векторами, направленными по координатным осям.
Матрицы вращения могут быть установлены вокруг осей i, j, k, в зависимости от того, какие векторы хотят повернуться. Для примера: если вектор должен повернуться около оси k, то будет использоваться матрица вращения, содержащая элементы i и j. С помощью этой матрицы можно повернуть направление вектора на заданный угол вокруг оси k.
Таким образом, использование базиса ijk позволяет с большой точностью задавать повороты в трехмерном пространстве. Это находит широкое применение в графике и трехмерной компьютерной графике.
- Базис ijk образуется векторами по координатным осям
- Матрицы вращения устанавливаются вокруг осей i, j, k
- Эти матрицы могут поворачивать векторы на заданный угол
Таким образом, базис ijk и матрицы вращения являются важной частью математического аппарата работы с трехмерным пространством. Они позволяют удобно и эффективно задавать движения объектов и систем объектов в трехмерном пространстве.
ijk и кватернионы
Кватернионы – это расширение комплексных чисел, которые, в свою очередь, являются расширением действительных чисел. Кватернионы были изобретены в XIX веке ученым Уильямом Гамильтоном. Наиболее известным свойством кватернионов является возможность выполнить вращение в трехмерном пространстве, используя всего четыре числа.
Кватернионы состоят из четырех элементов и обозначаются как q = w + xi + yj + zk, где w, x, y и z – это действительные числа, а i, j и k – это мнимые единицы, удовлетворяющие свойствам:
- i^2 = j^2 = k^2 = ijk = -1
- ij = k, ji = -k
- jk = i, kj = -i
- ki = j, ik = -j
Мнимые единицы i, j и k в кватернионах используются для представления 3-х мерного вектора, направленного вдоль осей x, y и z соответственно. Вектор i представляет направление вдоль оси x, j вдоль оси y и k вдоль оси z.
Ijk – это три элемента кватерниона, которые являются произведением мнимых единиц jk, ij и ki. Исходя из свойств мнимых единиц кватернионов, ijk = -1, что делает ijk очень важным в рассмотрении кватернионов.
Вместе с i, j и k, ijk играет важную роль в определении вращений в трехмерном пространстве. Кватернионное представление векторных вращений использует выражение в виде q = cos(θ/2) + u*sin(θ/2), где cos(θ/2) – действительная часть кватерниона, u – вектор вращения, представленный в виде b*i + c*j + d*k и sin(θ/2) – мнимая часть кватерниона.
ijk и геометрия
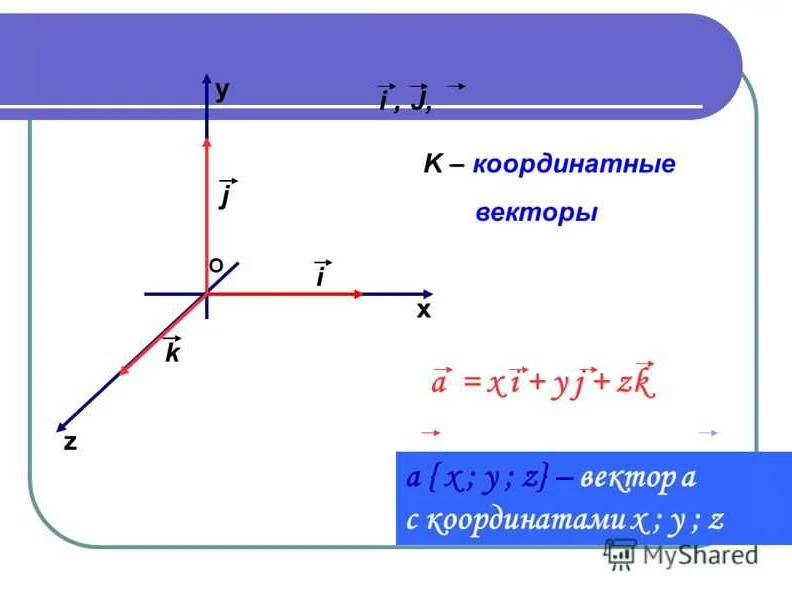
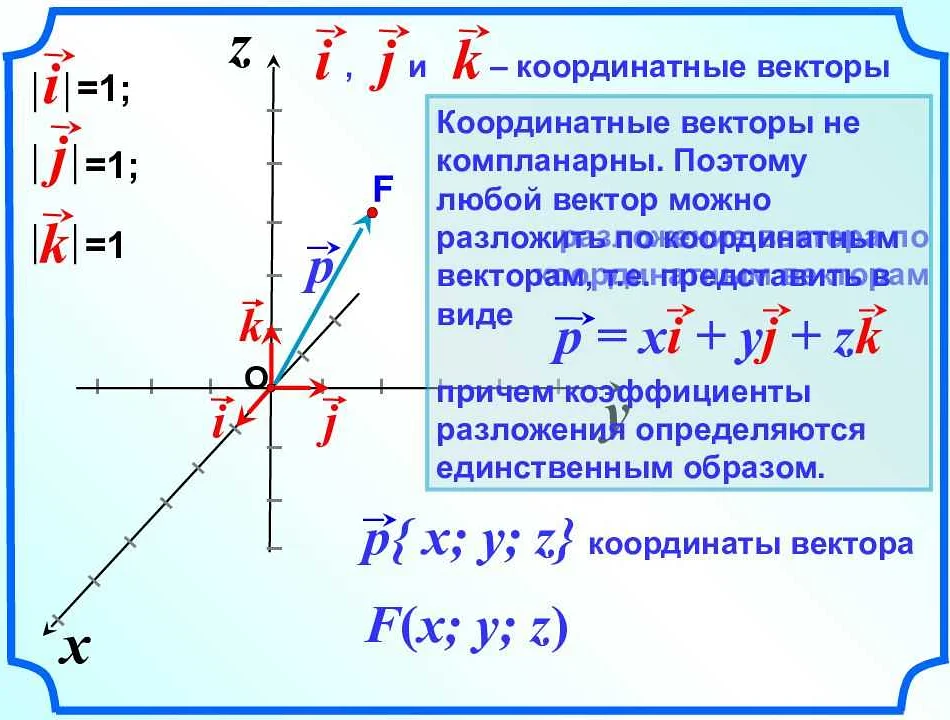
ijk – это система координат, используемая в трехмерной геометрии. Каждому вектору в пространстве соответствует уникальный набор чисел ijk. Эти числа обозначают координаты вектора вдоль осей x, y и z соответственно.
В системе ijk каждая ось является перпендикулярной к другим двум осям. Ось i соответствует направлению вправо, ось j соответствует направлению вверх, а ось k соответствует направлению вглубь. Таким образом, если мы знаем ijk-координаты вектора, мы можем легко определить его положение в пространстве.
Для работы с ijk-координатами вектора можно использовать матричные операции, такие как произведение матриц и транспонирование. Эти операции позволяют легко вычислять углы между векторами, длины и направления векторов.
Использование системы ijk в геометрии позволяет решать широкий спектр задач, связанных с вычислением расстояний в пространстве, определением направления движения объектов и т.д. Также ijk-координаты векторов используются в компьютерной графике для отображения трехмерных объектов в двухмерном пространстве.
ijk и аналитическая геометрия
ijk – это система координат, которая широко используется в аналитической геометрии, которая является одной из важных областей математики. В системе координат ijk каждая точка в пространстве задается тремя координатами, которые относятся к трем направлениям: x, y и z. Точка расположена в месте, где пересекаются все три оси.
Использование системы координат ijk делает возможным решение различных задач из аналитической геометрии, таких как определение расстояния между двумя точками, построение геометрических фигур в трехмерном пространстве и т.д.
ijk используется не только для решения задач в аналитической геометрии, но и в других областях, таких как физика, геодезия, геоинформатика и т.д. Расширение системы координат ijk в более высокие размерности также широко применяется в математике и ее приложениях.
Общая характеристика системы координат ijk – это она позволяет задать положение точки в трехмерном пространстве. Использование системы координат с тремя основными направлениями (ось x, y и z) важно для изучения различных пространственных объектов и связанной с ними математики. Кроме того, ijk система координат может быть используется в различных полях науки и инженерии для решения практических задач.
ijk и теория чисел

В теории чисел, ijk (или i+j=k) являются целыми числами, которые могут принимать только определенные значения. Другими словами, ijk образуют ограниченное множество чисел, которое может быть использовано для решения математических проблем.
Обычно i, j и k соответствуют числам -1, 0 и 1. Но их можно заменить на другие числа или даже на алгебраические выражения, если это необходимо для решения конкретной задачи в теории чисел. Часто ijk используются для изучения свойств кольца целых чисел и его идеалов.
Другой важной областью, связанной с ijk, является групповая теория. В групповой теории ijk могут рассматриваться как элементы группы, которые могут быть комбинированы с помощью операций сложения и умножения. Это позволяет использовать групповую теорию для изучения свойств ijk и их взаимодействий.
ijk также играют важную роль в теории формальных языков и автоматов. Например, ijk могут быть использованы для создания контекстно-свободных грамматик и конечных автоматов, которые могут использоваться для анализа и обработки языковых конструкций и данных.
В целом, ijk представляют собой удобное и мощное средство для изучения различных вопросов в теории чисел, групповой теории и формальных языках. Их широкое использование и вариативность их применения позволяют исследователям этих областей продвигаться вперед в своих исследованиях и расширять свои знания и компетенции.
ijk и компьютерная графика
Буквы i, j и k широко используются в математике и физике для обозначения векторов и операций над ними. В компьютерной графике эти буквы также играют важную роль при работе с трехмерными моделями.
В компьютерной графике система координат обычно состоит из трех осей: оси x, y и z, которые соответствуют направлениям вдоль горизонтальной, вертикальной и глубинной осей. Векторы i, j и k определяют направление каждой из этих осей соответственно. Например, вектор i направлен вдоль оси x, j – вдоль оси y, а k – вдоль оси z.
Таким образом, вектор в компьютерной графике может быть представлен в виде (x, y, z), где x, y и z – это проекции вектора на оси i, j и k соответственно. При работе с трехмерными моделями также используются линейные комбинации векторов i, j и k для задания направления поверхности и определения перспективы.
Кроме того, векторы i, j и k и их комбинации широко используются в различных алгоритмах компьютерной графики, таких как алгоритмы рендеринга, анимации и моделирования физических процессов.
Применение ijk в реальной жизни
Алгебраические системы, основанные на числах i, j и k, находят применение во многих областях науки. Например, комплексные числа или кватернионы используются в электротехнике, физике и компьютерной графике.
Одно из наиболее ярких применений ijk – использование кватернионов в автоматических системах управления. Например, кватернионные фильтры применяются в навигации и управлении беспилотными авиалайнерами, роботами и другими технологическими объектами.
Еще один пример применения ijk связан синтезом музыки. Некоторые инструменты, такие как клавишные, имеют возможность изменять звук в соответствии с движением музыканта. Таким образом, управление звуком связано с изменением положения в пространстве, а значит, в качестве базиса для описания таких изменений может использоваться трехмерное пространство ijk.
Также ijk находит применение в компьютерных играх. Например, для реализации трехмерного взаимодействия с объектами и персонажами игры используются кватернионы.
Также стоит отметить, что ijk – важный инструмент для математических исследований, связанных с геометрией и анализом многомерных пространств. Полученные при различных исследованиях результаты позволили расширить возможности математики и создать новые методы анализа данных.
Вопрос-ответ:
Что означает ijk в математике?
В математике ijk обозначают базисные векторы в трехмерном пространстве. i – вектор, направленный вдоль оси x, j – вектор, направленный вдоль оси y, k – вектор, направленный вдоль оси z.
Какие свойства имеют базисные векторы ijk?
Основное свойство базисных векторов ijk – ортогональность. То есть векторы ijk перпендикулярны между собой. Кроме того, они единичной длины, то есть |i| = |j| = |k| = 1.
Как использовать базисные векторы ijk для задания вектора в трехмерном пространстве?
Чтобы задать вектор в трехмерном пространстве, нужно указать его координаты по осям x, y и z. Координаты вектора задаются как скалярные произведения вектора на базисные векторы ijk. То есть если вектор имеет координаты (a, b, c), то он может быть представлен как a*i + b*j + c*k.
Можно ли использовать другие буквы вместо ijk для обозначения базисных векторов?
Да, в качестве обозначения базисных векторов можно использовать любые другие символы или буквы. Однако ijk являются стандартными обозначениями, которые широко используются в литературе и в учебных пособиях.
Какие преобразования можно выполнять с базисными векторами ijk?
С базисными векторами ijk можно выполнять линейные преобразования. Например, можно умножать их на константы, складывать и вычитать, а также вращать и переводить. При этом необходимо учитывать их свойства – ортогональность и единичную длину.
Какие математические объекты могут быть представлены в виде комбинации базисных векторов ijk?
Базисные векторы ijk могут быть использованы для представления векторов, матриц, кватернионов и других математических объектов в трехмерном пространстве. Векторы и матрицы представляются в виде линейной комбинации базисных векторов, а кватернионы – в виде комбинации базисных векторов и вещественного скаляра.
Как использовать базисные векторы ijk в геометрии?
Базисные векторы ijk используются в геометрических задачах для расчета расстояний, углов, площадей и объемов. Например, чтобы найти расстояние между двумя точками в трехмерном пространстве, можно представить их координаты в виде векторов и вычислить длину разности векторов. Также с помощью базисных векторов можно задавать направления и повороты в пространстве.






