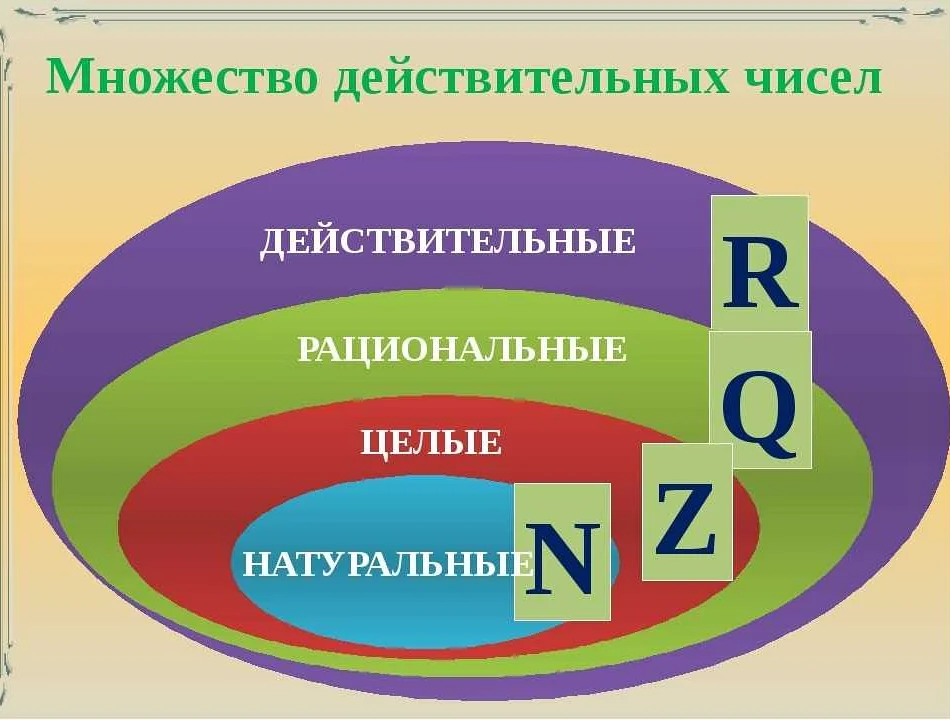
N в математике может обозначать различные величины, в зависимости от контекста. Это может быть натуральное число или переменная, принимающая числовые значения. Также буква n используется для обозначения размерности множества или матрицы. Узнайте, какую задачу решает буква n в вашей формуле или выражении, в статье на сайте.
Математика считается одним из наиболее строгих и точных наук, в которой каждое обозначение имеет своё точное значение и название. В этой науке широко используются символы и буквы, имеющие своё определенное значение. Одной из таких букв является буква n, которая в математике обозначает различные значения в зависимости от контекста использования.
Буква n является переменной и может принимать различные значения, что сильно зависит от того, в какой формуле она используется. Например, в алгебре, буква n является обозначением натурального числа, тогда как в аналитической геометрии – переменной для обозначения координат точки на плоскости.
Также буква n может использоваться в математике в качестве индекса или суммационного знака, обозначающего конечную сумму элементов последовательности. Этот символ используется в таких разделах математики, как теория вероятностей, анализ, теория комбинаторов и других математических областях.
Понятие
В математике понятие является основой любой теории и представляет собой абстрактную, определенную и общую идею, охватывающую множество конкретных объектов или явлений.
Одно из важных свойств понятия в математике – это его формализованность. Конкретный объект описывается при помощи понятия, которое формализовано с помощью определений и аксиом.
Обычно понятия в математике обозначаются символами, что позволяет удобнее и точнее записывать математические формулы и теоремы. Например, буква n используется для обозначения целочисленных переменных или параметров в формулах.
Понятия в математике используются для построения систем и теорий, и образуют связанные между собой концепции. Важно понимать, что понятия являются абстрактными идеями, заложенными в основе математических конструкций и теорий, и не имеют прямого отношения к физическому миру.
- Изучение математических понятий позволяет развивать абстрактное мышление и логическое мышление, что также может быть полезно в других областях жизни.
- Одним из важных элементов изучения понятий в математике является понимание их подразделений, включая определения, абстрактные структуры, примеры, контр-примеры и общие свойства.
Алгебра
Алгебра – это раздел математики, который изучает общие законы и правила преобразования алгебраических выражений. Эта дисциплина занимается решением уравнений, операциями с многочленами, функциями и их графиками.
Алгебра включает множество базовых понятий, таких как переменные, коэффициенты, степени, скобки, многочлены, алгебраические уравнения и т.д. Все эти понятия используются в алгебре для решения различных задач и создания математических моделей.
Одним из ключевых понятий алгебры является алгебраический многочлен. Это выражение, состоящее из коэффициентов и переменных, взятых в определенные степени. При решении уравнений и других задач алгебра использует именно такие многочлены.
- Алгебра также широко используется в других областях математики, включая геометрию, топологию, анализ и теорию чисел.
- Одним из важных элементов алгебры являются матрицы. Это таблицы чисел, используемые для решения систем уравнений, линейных преобразований и других задач.
- Алгебра также полезна для создания компьютерных программ и алгоритмов в разных областях, включая физику, экономику и инженерию.
Таким образом, алгебра является фундаментальной дисциплиной математики, которая широко используется в науке, технологиях и многих других областях знаний.
Геометрия
Геометрия – раздел математики, изучающий фигуры, их свойства, взаимное расположение и преобразования. Среди главных объектов геометрии – точки, прямые, плоскости, углы и многогранники.
Одним из важнейших понятий в геометрии является расстояние между двумя точками. Оно определяется как длина кратчайшего пути между ними, и играет ключевую роль во многих задачах геометрии.
Геометрия включает в себя множество теорем и правил, позволяющих решать задачи на построение или доказательство свойств различных фигур. Также геометрия находит свое применение в различных областях, в том числе в физике, инженерии, компьютерной графике и дизайне.
- В геометрии используются такие понятия, как прямая, плоскость, угол, треугольник, круг, конус, цилиндр и многие другие;
- Геометрия имеет строгую логическую структуру, основанную на аксиомах и доказательствах;
- Среди важнейших теорем геометрии можно выделить, например, теорему Пифагора, теорему Фалеса и теорему о трех перпендикулярах;
- Современная геометрия включает в себя различные разделы, в том числе дифференциальную геометрию, топологию и алгебраическую геометрию.
Тригонометрия
Тригонометрия – это раздел математики, который занимается изучением свойств и закономерностей прямоугольных и непрямоугольных треугольников. Главными тригонометрическими функциями являются синус, косинус и тангенс, которые используются для расчетов угла, длины сторон и других характеристик треугольников.
Синус – это отношение противоположной стороны к гипотенузе в прямоугольном треугольнике. Обозначается символом sin.
Косинус – это отношение прилегающей стороны к гипотенузе в прямоугольном треугольнике. Обозначается символом cos.
Тангенс – это отношение противоположной стороны к прилегающей стороне в прямоугольном треугольнике. Обозначается символом tan.
Тригонометрию широко применяют в геометрии, физике, инженерии и других науках, которые требуют решения задач, связанных с треугольниками и углами. Также тригонометрия является основой для более сложных математических концепций, таких как анализ функций и дифференциальные уравнения.
- Обратные тригонометрические функции
Кроме основных тригонометрических функций, существуют обратные тригонометрические функции, такие как арксинус, арккосинус и арктангенс. Они используются для нахождения углов, если известны соответствующие значения тригонометрических функций.
- Таблица значений тригонометрических функций
Угол (градусы)СинусКосинусТангенс
| 0 | 0 | 1 | 0 |
| 30 | 0.5 | 0.87 | 0.58 |
| 45 | 0.71 | 0.71 | 1 |
| 60 | 0.87 | 0.5 | 1.73 |
| 90 | 1 | 0 | н/д |
Таблица значений тригонометрических функций – это инструмент, который используется для быстрого определения значений синуса, косинуса и тангенса наиболее распространенных углов.
Математический анализ
Математический анализ – это раздел математики, который изучает функции, пределы, производные и интегралы.
Основные задачи математического анализа – это нахождение пределов функций, определение производных и интегралов различных функций. Эти задачи важны не только в математике, но и в других областях науки, таких как физика и инженерия.
Производная – это показатель изменения функции в точке. Она используется для определения экстремумов функций и построения касательных к графику функции в точке.
Интеграл – это площадь под графиком функции. Интегралы используются для нахождения площади фигур и объемов тел, а также для решения уравнений в физике и инженерии.
Математический анализ является одним из основных курсов высшей математики на уровне бакалавриата во многих учебных заведениях.
- Основные понятия математического анализа:
- Функция
- Предел
- Производная
- Интеграл
- Практическое использование математического анализа в различных областях науки и техники
- Экзаменационные вопросы, задачи и тесты по математическому анализу
Математический анализ – это важный курс, который подготавливает студентов к применению математических методов в решении научных и инженерных задач. Он также помогает в развитии логического мышления, аналитического и пространственного мышления.
Теория вероятности
Теория вероятности – раздел математики, изучающий вероятность событий и случайные явления. Она находит широкое применение в физике, статистике, экономике, биологии и других науках.
В теории вероятности основными понятиями являются вероятность, случайная величина и распределение вероятностей. Вероятность события – это шанс или возможность того, что оно произойдет. Случайная величина – это переменная, которая принимает различные значения в результате случайного события. Распределение вероятностей определяет вероятность того, что случайная величина примет определенное значение.
Теория вероятности используется для оценки вероятности различных событий и для создания математических моделей, которые помогают предсказывать результаты случайных экспериментов. Например, она может помочь оценить вероятность появления определенной группы генов в популяции, вероятность того, что определенный материал обладает определенными свойствами, или вероятность успешной продажи определенного продукта на рынке.
Теория вероятности имеет множество приложений и проявлений в различных областях науки и техники. Она помогает принимать взвешенные решения на основе анализа статистических данных и их вероятностных сценариев. Поэтому, при изучении математики, теория вероятности занимает важное место и является необходимой для расширения парка инструментов для решения задач.
Комбинаторика
Комбинаторика – это раздел математики, который изучает различные комбинации и перестановки элементов. Она использует различные методы и формулы для анализа и определения количества возможных комбинаций.
Основными понятиями комбинаторики являются перестановки, сочетания и размещения. Перестановки – это упорядоченные комбинации элементов. Сочетания – это комбинации элементов без порядка. Размещения – это комбинации элементов с учетом порядка и повторений. Каждый тип комбинации имеет свои формулы и правила.
Комбинаторика используется в различных областях, включая статистику, экономику, информатику и физику. Также она является основой для решения многих задач в реальной жизни, таких как определение вероятности событий и различных комбинаций в играх и спорте.
- Формула перестановок – n! (n-факториал)
- Формула сочетаний – C(n,k) = n!/k!(n-k)!
- Формула размещений – A(n,k) = n!/(n-k)!
Важно понимать, что комбинаторика может быть сложной и существует множество подводных камней. Необходимо правильно применять формулы и учитывать все условия задачи.
Тип комбинацииФормулаПример
| Перестановки | n! | Для 4 элементов – 4! = 24 |
| Сочетания | C(n,k) = n!/k!(n-k)! | Для 5 элементов выбрать 3 – C(5,3) = 10 |
| Размещения | A(n,k) = n!/(n-k)! | Для 7 элементов выбрать 4 с учетом порядка – A(7,4) = 840 |
Математическая логика
Математическая логика – это раздел математики, изучающий формальную структуру математических высказываний и методы их доказательства или опровержения. Она используется в различных областях, таких как информатика, философия и теория алгоритмов.
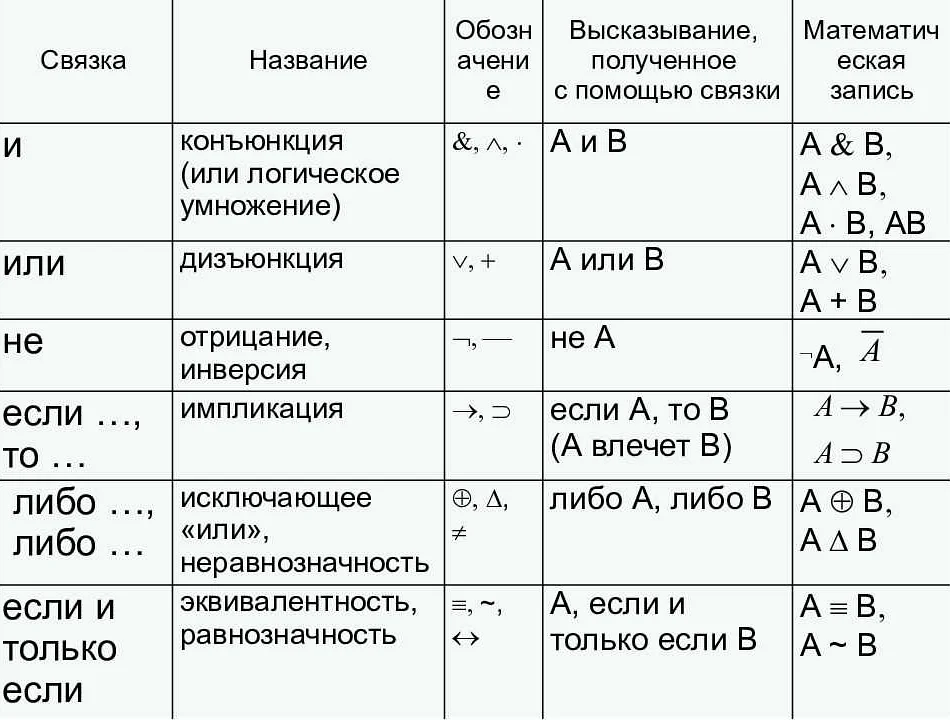
Важным понятием в математической логике является «логическая связка». Это термин, обозначающий способ, которым два или более высказывания соединяются для создания комплексного высказывания. К примеру, связки «и», «или», «отрицание» и «следствие» – это некоторые наиболее распространенные логические связки.
Математическая логика используется в теории вероятностей, когда требуется определить точность результатов, в теории алгоритмов, для доказательства правильности работы программ и для исследования математических гипотез. Более того, методы математической логики можно использовать для разработки методов решения различных логических и математических задач.
Математическая логика является одним из центральных направлений в современной теории заключений, синтаксическом методом принятия решений, рекомендуемым для использования в социальных науках, методом машинного обучения и работе с искусственным интеллектом.
Функции и их применение
Функция – это математический объект, который принимает одно или несколько значений и возвращает новое значение. Они широко используются в различных областях науки и техники, таких как физика, экономика, компьютерное программирование и др.
Одной из основных применений функций является моделирование реальных процессов и явлений. Например, для описания движения тела в физике используются функции, которые описывают, как изменяется скорость и позиция тела во времени.
В экономике функции используются для определения стоимости товаров, расчета прибыли и рентабельности бизнеса. Также они используются в финансовых моделях для прогнозирования изменений курса валют и цен.
В компьютерном программировании функции используются для различных целей, таких как обработка данных, управление потоком выполнения программы и создание пользовательских интерфейсов.
Функции могут быть записаны в виде формул, таблиц или графиков, что позволяет описывать их свойства и производить вычисления. Они являются важным инструментом для решения различных задач и могут быть использованы на практике для получения конкретных результатов.
Формулы и их использование
В математике формулы используются для описания различных явлений и процессов. Они помогают связать между собой различные переменные и определения, что позволяет нам более точно и эффективно работать с числовыми значениями и прогнозировать результаты.
Формулы могут быть простыми или сложными, они могут использоваться в различных областях наук и техники. Например, формула кинетической энергии E = (m*v^2)/2 используется в физике для расчета энергии движения, а формула для расчета площади круга S = π*r^2 является базовой формулой геометрии.
Формулы могут быть представлены в виде таблиц, графиков, диаграмм и прочего. Они могут быть выполнены исходя из строгих matemathical принципов или же образом эвристически, имея большую степень приближения.
Важным аспектом работы с формулами является их правильное использование и интерпретация. Даже небольшая ошибка в расчете результатов может привести к серьезным ошибкам. В этом случае может быть полезен специальный математический софт для проверки точности и грамотности в данных расчетах.
Примеры использования
n как переменная в математике: N может использоваться как переменная в алгебре, геометрии и других областях математики. Например, если у вас есть формула для вычисления площади прямоугольника, то n мог бы быть использован для обозначения одной из его сторон.
n как порядковый номер: Когда мы говорим о n-й степени числа или n-м члене последовательности, мы используем n для обозначения порядкового номера. Например, третье число в последовательности Фибоначчи – это число, которое мы получим, если пройдем по последовательности и посчитаем до n = 3.
n как связь с комплексными числами: Когда мы говорим о комплексных числах, мы обычно используем букву “i” для обозначения мнимой единицы. Однако, иногда мы можем использовать букву “n”, чтобы обозначить множитель при мнимой единице. Например, комплексное число 3 + 4i может быть записано как 3 + 4n.
n как размерность матрицы: В линейной алгебре мы можем использовать букву “n” для обозначения размерности матрицы. Например, если у нас есть матрица размером 3 на 3, то мы можем записать ее как A3x3.
- n как порядковый номер
- n как переменная
- n как связь с комплексными числами
- n как размерность матрицы
Вопрос-ответ:
Зачем в математике используют символ n?
Символ n в математике является переменной, которая обозначает любое натуральное число. Его часто используют для обозначения количества элементов в последовательности, множестве или других математических объектах.
Можно ли использовать другие символы вместо n?
Да, в математике можно использовать любые символы в качестве переменных. Однако символ n остается наиболее распространенным, так как он ассоциируется с натуральными числами.
Каким образом символ n используется в теории графов?
В теории графов символ n используется для обозначения количества вершин в графе. Например, граф с 5 вершинами будет обозначаться как G = (V, E), где V = {1,2,3,4,5} и E – множество ребер.
Какие другие математические понятия связаны с символом n?
Символ n часто используется в комбинаторике, теории вероятности и теории чисел. Например, в комбинаторике n! (n-факториал) обозначает произведение всех натуральных чисел от 1 до n включительно, а в теории вероятности иногда используется обозначение P(n) – вероятность наступления события n.
Можно ли использовать символ n в других областях науки, вне математики?
Да, символ n может использоваться в любой области науки, где требуется обозначить некоторое количество. Например, в физике символ n может использоваться для обозначения числа частиц в некотором объеме, а в информатике – для обозначения размера массивов и других структур данных.
Есть ли какие-то ограничения на использование символа n в математике?
Нет, символ n может использоваться в математике без каких-либо ограничений. Однако, при использовании его в некоторых областях математики, следует учитывать контекст и не перепутать его с другими переменными или обозначениями.
В чем отличие символа n от буквы m?
Символ n всегда обозначает натуральное число, тогда как буква m может обозначать любое другое фиксированное число или переменное значение. В некоторых случаях, например в комбинаторике, m также может обозначать номер элемента в последовательности, но область применения символа n гораздо шире.






