Пи (π) – это математическая константа, обозначающая отношение длины окружности к ее диаметру. Эта константа имеет бесконечную десятичную дробь, начинающуюся с 3,14, но без конечного периода. Пи используется в геометрии, анализе, теории вероятностей и других областях математики для решения множества задач и формул. Узнайте больше о пи в статье на нашем сайте.
Если вы когда-либо учили математику, то вы должны были столкнуться с числом π. Оно широко используется в геометрии, физике и инженерии для расчетов окружностей, сфер и других круговых форм. Но что это за число и почему оно так важно?
Пи – это математическая константа, которая представляет собой отношение длины окружности к ее диаметру. Его значение почти равно 3.14159, но оно бесконечно длинное, и ученые всегда пытаются вычислить его точнее.
Хотя π часто используется для расчетов геометрических фигур, его можно написать еще многими другими способами. Оно также является суммой ряда, подстрокой числа e (основание натурального логарифма) и многим другим.
Узнаем, что такое число pi
Число pi – это математическая константа, которая обозначает отношение длины окружности к ее диаметру. Оно обозначается греческой буквой π.
Число pi является иррациональным числом, то есть оно не может быть выражено как дробь и его десятичные знаки не повторяются. Поэтому значение pi может быть вычислено только приближенно с определенной точностью.
Число pi встречается во многих областях математики, физики и инженерии. Оно используется в формулах для вычисления площади круга и объема шара, а также в решении задач, связанных с волнами, теорией вероятности и статистикой.
- Значение pi составляет приблизительно 3,14159.
- Значение pi было известно еще в древности. В Древнем Египте его значение было приблизительно равно 3,16.
- В 2009 году японский математик Масамити Сага Шибатани вычислил значение pi с точностью до 5 триллионов знаков после запятой.
Как и когда появилось число pi
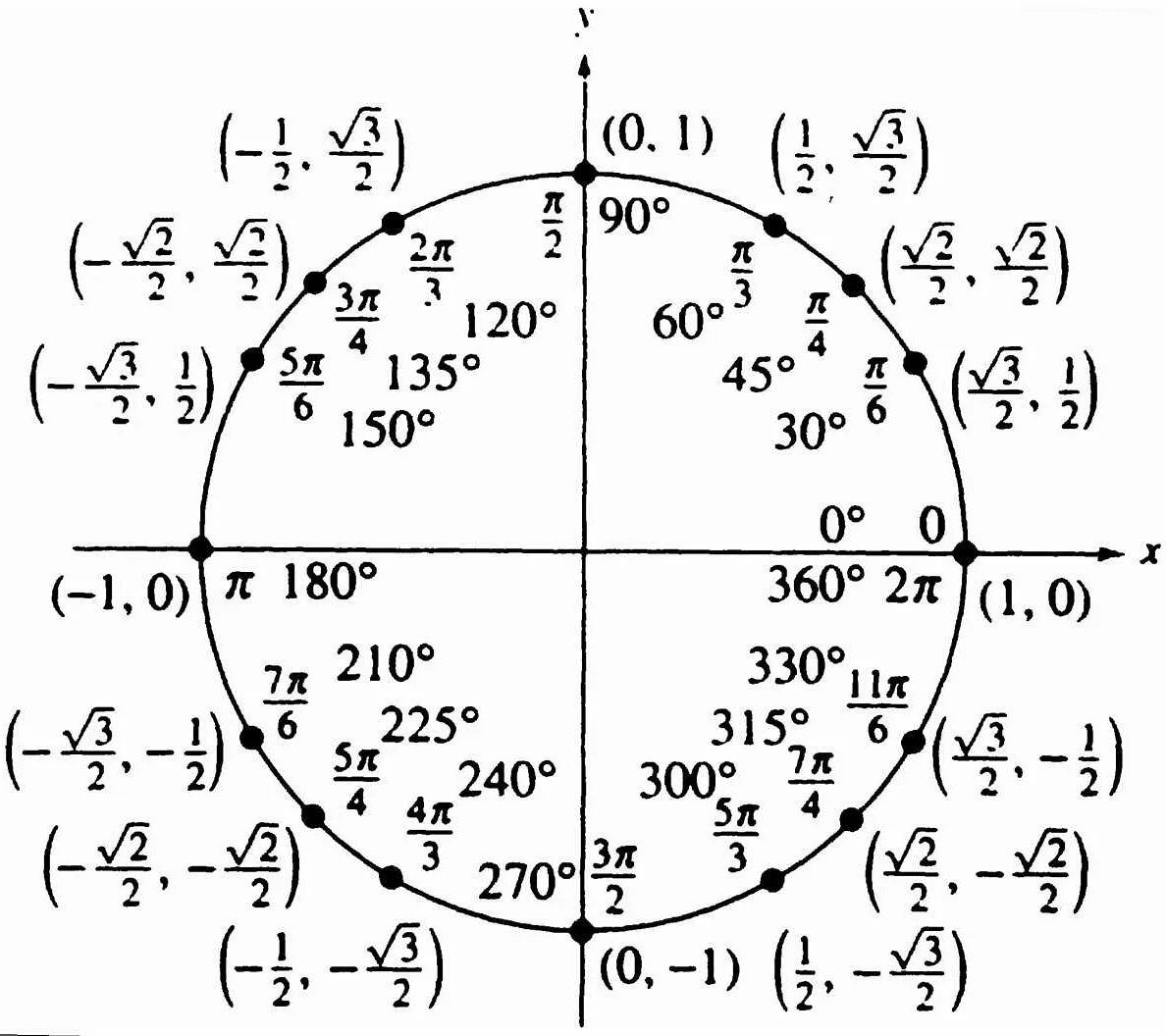
Число pi, обозначающее отношение длины окружности к ее диаметру, было известно с древних времен. Один из первых упоминаний о нем найдено в древнебабилонских таблицах, датированных приблизительно 1900 годом до нашей эры. Там число pi было приближенно равно 3.125.
В Египте аналогичные приближенные числа были записаны в папирусах Единой системы измерений, датированных XIV до нашей эры. А в Древней Греции число pi относилось к серии архитектурных задач и появлялось как результат геометрических вычислений в учебных пособиях.
Более точные значения числа pi нашли арабские математики в VIII веке. Один из них, астроном, математик и инженер Аль-Хваризми, который жил в Багдаде, получил число pi равным 3,1416. В смежной области математики – тригонометрии – арабские математики также внесли значительный вклад в развитие математики.
Существуют различные методы расчета числа pi, которые используются в математике и научных исследованиях до сих пор. Одним из наиболее известных является метод Монте-Карло, который используется для аппроксимации сложных и непредсказуемых функций.
Зачем нужно число pi в математике
Число π является одним из самых важных математических констант. Оно используется во многих областях науки и техники, включая физику, инженерное дело и компьютерную графику.
Наиболее известное свойство числа π заключается в том, что оно является отношением длины окружности к ее диаметру. Это означает, что π используется в формулах для вычисления длины окружности, площади круга и объема шара. Это очень важно для специалистов в области архитектуры, инженерии и физики, которые используют числовые значения π для расчета размеров и возможностей объектов.
Технологический прогресс был бы невозможен без числа π. Оно используется в различных компьютерных алгоритмах, включая алгоритмы сжатия изображений, обработки сигналов и кодирования данных. Без π вычисление было бы невозможно, и это привело бы к невозможности использования многих современных технологий.
Число π также используется в математических исследованиях, связанных с геометрией, топологией и анализом. Оно является ключевым элементом в ряде формул и теорем, которые используются в математических исследованиях, и имеет непосредственное отношение к научным и инженерным задачам.
В целом, число π не только является одним из самых важных математических констант, но и является важным элементом в науке и технологии. Без π всегда было бы невозможно решать многие математические и инженерные задачи, что означает, что его значимость продолжит расти в будущем.
Как вычислить число pi
Число пи является константой, которая представляет собой отношение окружности к её диаметру. Её значение равно 3.14159265358979323846264338327950288419… Однако, точное значение числа пи не может быть представлено конечным количеством знаков. Вместо этого его можно приблизительно вычислить. Существует множество методов для приближенного вычисления числа пи.
Один из методов, называемый “методом Монте-Карло”, заключается в том, чтобы случайным образом выбирать точки внутри единичного круга и подсчитывать их отношение к общему количеству точек. С увеличением количества точек, это отношение будет приближаться к значению числа пи.
Другой метод, называемый “методом Архимеда”, использует последовательность многоугольников, описанных вокруг единичной окружности, для вычисления числа пи. Чем больше количество сторон многоугольника, тем ближе его периметр к окружности, и тем точнее может быть приблизительно вычислено число пи.
Существует также множество других методов, включая использование ряда Лейбница и использование интегралов.
- Метод Монте-Карло: случайно выбрать точку внутри единичного круга и подсчитать её отношение к общему количеству точек. Повторить N раз. Число пи будет примерно равно 4 * (количество точек, попавших в круг) / N.
- Метод Архимеда: начать с многоугольника, описанного вокруг единичной окружности с большим количеством сторон. Постепенно увеличивать количество сторон, пересчитывая периметр каждый раз. При достаточном количестве сторон полученный периметр будет близок к длине окружности, а число пи – близко к отношению длины окружности к диаметру (периметр / 2).
Как записать число pi

Число pi обозначается греческой буквой π (альфа-фонтика — пи). Если вы хотите использовать символ π при написании математических выражений, то можете воспользоваться символом Unicode U + 03C0 (без кавычек) или HTML-кодом π.
Также вы можете записать число pi в десятичном виде, но учтите, что число pi — бесконечная десятичная дробь, поэтому стандартное округление числа pi равно 3.14159265358979323846. В зависимости от необходимой точности в вычислениях, число pi можно округлять до нужного количества знаков.
Для записи числа pi в технических документах может быть использована стандартная запись ISO 80000-2:2009, где pi записывается как π (без дополнительных символов).
Еще один способ записи числа pi – использование выражения “круговой диаметр”. В этом случае, pi представляет собой отношение длины окружности к ее диаметру и записывается как pi = Д/О.
Таким образом, число pi может быть записано разными способами в зависимости от цели его использования. Оно является одним из важнейших математических констант и используется во многих областях науки и техники.
Известные задачи, связанные с числом pi
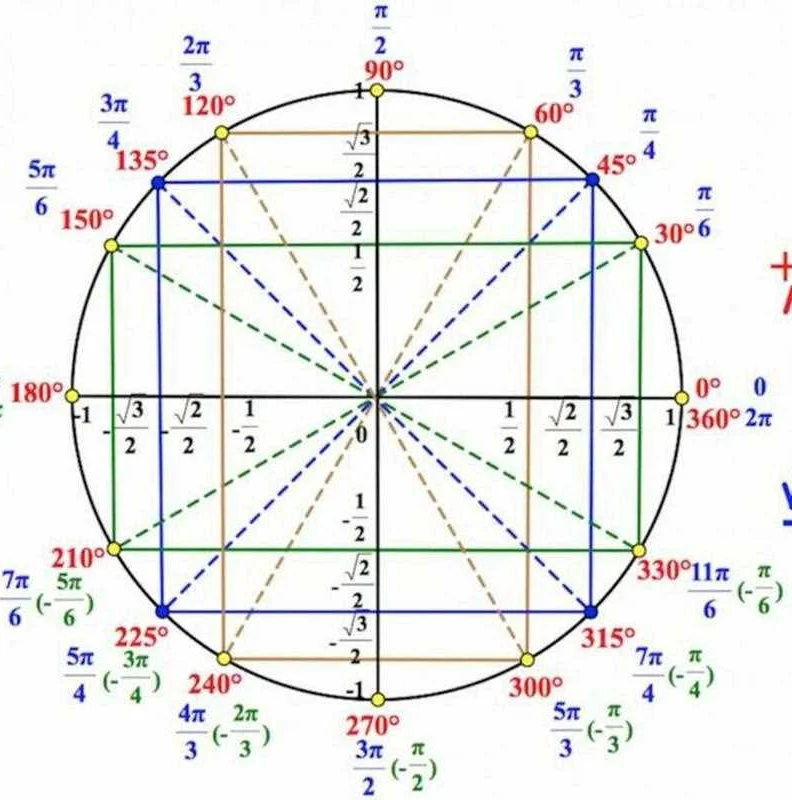
Вычисление числа pi
Задача нахождения точной величины числа pi является одной из самых известных задач математики. Для многих веков ученые пытались приблизиться к точной величине pi. В настоящее время для вычисления числа pi существуют различные методы, включая способы, использующие базовые арифметические операции и компьютерные алгоритмы. Одним из наиболее известных методов является формула Лейбница, которая предполагает вычисление pi при помощи ряда из бесконечного количества слагаемых.
Измерение обхвата Земли
Одна из первых задач, связанных с числом pi, была связана с измерением обхвата Земли. Известный древнегреческий ученый Эратосфен предложил найти обхват Земли, используя измерение угла между лучами солнца, падающими на двух точках различных городов. Полученное значение угла и расстояние между городами позволили Эратосфену приблизительно определить длину окружности Земли, а значит и число pi.
Квадратуры круга
Задача квадратуры круга заключается в том, чтобы найти площадь круга с помощью конечного числа арифметических операций. В течение многих веков многие ученые пытались решить эту задачу, но существует математическое доказательство, что невозможно построить квадрат, площадь которого будет точно равна площади круга. Кроме того, доказано, что задача квадратуры круга сводится к вычислению числа pi с определенной степенью точности.
Парадокс Банаха-Тарского
Парадокс Банаха-Тарского – это необычная математическая задача, связанная со свойствами бесконечности и геометрических преобразований. В том, что это задача, связанная с числом pi, можно убедиться, рассмотрев так называемую “конструкцию Банаха-Тарского”, которая позволяет использовать бесконечно малые значения pi для разбивки и склеивания объектов без потери их объема.
Сформулированные гипотезы
Существуют несколько гипотез, связанных с числом pi, которые предполагают, что десятичные цифры pi никогда не повторяются, что число pi является нормальным или что для него верна гипотеза Берри о равномерности распределения цифр.
Необычные факты о числе pi
Число pi является одним из самых известных математических констант. С помощью него можно вычислять длины окружностей, площади кругов и другие геометрические характеристики.
Но все мы знаем это. А сейчас я хочу рассказать вам о нескольких необычных фактах о числе pi.
- Число pi является бесконечным. Мы можем вычислить его первые несколько знаков после запятой (3,14159265359…), но на самом деле число pi имеет бесконечную десятичную дробь.
- Число pi является иррациональным. Это означает, что его десятичная дробь не может быть выражена как отношение двух целых чисел.
- Число pi появляется в самых неожиданных местах. Например, в формуле для вычисления площади правильного многоугольника (S = (1/2)Pa)). Когда количество сторон многоугольника стремится к бесконечности, мы получаем формулу для площади круга, в которой фигурирует число pi.
Еще один факт, который не относится непосредственно к числу pi, но связан с ним, — это День числа pi (14 марта). В этот день люди празднуют и используют свойства числа pi, испекая круглый пирог или проводя конкурсы и соревнования на знание знаков после запятой числа pi.
Число pi — удивительная математическая константа, которая поражает своей бесконечностью и встречается там, где мы ее не ожидаем. Вы, наверное, уже догадались, что она не оставит равнодушными ни математиков, ни людей, просто интересующихся наукой.
Использование числа pi в науке и технике
Число pi – это одно из самых известных и используемых математических констант. Оно используется в различных областях, включая науку и технику.
В науке:
- В геометрии: pi является соотношением длины окружности и ее диаметра, что позволяет его использовать для вычисления площади и объема различных фигур.
- В физике: pi применяется для вычисления периодических явлений, таких как электрический ток в колебательных контурах, колебания мембран и других.
- В астрономии: используются формулы, в которых фигурирует pi, для вычисления длины орбит различных небесных тел.
В технике:
- В строительстве: pi используется для вычисления объема различных конструкций, таких как шары, сферы и другие.
- В электронике: pi используется как часть формул для вычисления емкости и индуктивности различных электрических компонентов.
- В компьютерных науках: численное значение pi используется в алгоритмах вычисления и генерации случайных чисел.
В целом, число pi играет важную роль в науке и технике и используется для решения различных задач и вычислений.
Национальный день числа pi
14 марта отмечается Национальный день числа pi. Этот день был установлен в честь числа pi (π), которое является одним из наиболее известных и важных математических констант.
Число pi определяется как отношение длины окружности к ее диаметру в евклидовой геометрии. Это число является бесконечным десятичным дробным числом и начинается со значения 3,14. Число pi используется в различных областях математики, физики, инженерии, компьютерной графике и т.д.
Весь мир отмечает этот день с различными мероприятиями, в том числе, конкурсы на запоминание цифр числа pi до нескольких десятков, написание песен и стихов на тему pi, математические игры, тесты и т.д.
День pi является праздником для всех научных и инженерных сообществ по всему миру, и позволяет отметить важность математики для нашей повседневной жизни.
- 14 марта – Национальный день числа pi.
- pi – это одна из наиболее известных и важных математических констант.
- Число pi используется в различных областях математики, физики, инженерии, компьютерной графике и др.
- День pi отмечается различными мероприятиями по всему миру, включая математические игры, тесты и конкурсы на запоминание цифр числа pi до нескольких десятков.
Курьезные рекорды, связанные с числом pi
1. Большей точности мы еще не достигли
Число pi является иррациональным и бесконечным, поэтому его точное значение невозможно вычислить. Более того, мы уже добились огромной точности – 22,4 триллиона знаков! Для сравнения, общее количество пикселей на экране Retina MacBook составляет всего 5 миллионов.
2. Запомнить все знаки не могут даже айтишники
Запомнить все знаки числа pi не может даже самый загнанный айтишник. Однако это не мешает многим людям попробовать сделать это. В 2015 году, индийский математик и компьютерный инженер Санти Умапти (Suresh Kumar Sharma) попытался установить мировой рекорд по запоминанию знаков числа pi. Он вспомнил 70 000 знаков и занял второе место, но это был рекорд в Индии.
3. Музыкальные композиции на основе числа pi
Sean Murray, композитор из Великобритании, создал несколько музыкальных произведений на основе числа pi. В частности, одна из его композиций называется pi Symphony и имеет продолжительность в 3 часа и 14 минут (то есть, 3.14).
4. Использование числа pi для создания искусства
Ученые, математики и художники используют число pi для создания произведений искусства. Например, трикография Мартина Крумминга (Martin Kruming) называется “Пиксели числа pi” и состоит из более чем 400 000 точек, расположенных в порядке, заданном числом pi.
5. Юмористические праздники связанные с числом pi
14 марта (т.е. 3/14 в американском формате написания дат) часто называют Днем числа pi. В этот день люди часто едят пироги, играют в игры и проводят другие мероприятия, связанные с математикой и числом pi.
Вопрос-ответ:
Что такое число pi?
Число pi (π) – это дробное число, которое является математической константой и равно отношению длины окружности к её диаметру. Оно используется в различных областях математики, физики, статистики, инженерии и других науках.
Кто первым вычислил значение числа pi?
Первые вычисления значения числа pi относятся к древней индийской математике и датируются около 2 тысячелетия назад. Затем астроном и математик китайского происхождения Цзю Цун-цзы в 5 веке н.э. вычислил значение числа pi с точностью до 7 знаков после запятой. Значительно более точное значение числа pi было получено известным античным ученным Архимедом в III веке до н.э., который оценил его значение с точностью до двух десятичных знаков путем приближения к нему площади многоугольника, вписанного в круг и описанного вокруг круга.
Зачем нужно значение числа pi?
Значение числа pi находит применение в различных областях науки и техники, например, в геометрии, теории вероятности, физике, математическом анализе, алгебре и других областях. Оно используется для вычисления площади круга, объема шара, длины дуги окружности, периметра круга, угла поворота, среднего значения функций и др.
Как вычислить значение числа pi?
Существует несколько способов вычисления значения числа pi, например, метод Монте-Карло, формула Лейбница, формула Валлиса и др. Однако, все они дают лишь приближенное значение числа pi с определенной точностью.
Какая точность может быть достигнута при вычислении значения числа pi?
Точность при вычислении значения числа pi зависит от выбранного метода и количества вычислительных операций. Наилучшее значение точности, достигнутое на сегодняшний день, составляет более 31,4 триллиона десятичных знаков, которое было достигнуто в 2020 году с помощью специально разработанного программного обеспечения и суперкомпьютеров.
Какие применения числа pi можно найти в ежедневной жизни?
Значение числа pi используется в различных областях ежедневной жизни, например, в производстве электроники, где оно используется для вычисления частоты колебаний, в медицине для вычисления давления в артериях, в геодезии для измерения расстояний и углов, в статистике для анализа данных и т.д.
Каковы значения числа pi в разных системах счисления?
Значение числа pi не зависит от системы счисления и остается постоянным для любой системы счисления. Единственным отличием может быть способ записи числа pi в различных системах счисления. Например, в двоичной системе счисления число pi записывается как бесконечная периодическая дробь, а в шестнадцатеричной системе счисления число pi записывается как 3,14159265358979323846…
Почему число pi так важно в математике

Число pi – одна из наиболее уникальных и загадочных математических констант. Оно представляет собой отношение длины окружности к её диаметру.
Значение числа pi равно приблизительно 3,14159, но его десятичная запись бесконечна и не повторяется. Именно благодаря этому свойству число pi находится в основе многих математических, инженерных и научных вычислений.
Число pi появляется в самых разных областях науки. Например, оно используется в геометрии для вычисления объемов тел, площадей, периметров, в физике – при расчетах движения тел, в статистике и математическом анализе – при вычислении интегралов. Благодаря неразрывной связи числа pi с окружностями, оно находит применение в архитектуре, дизайне и других сферах.
Число pi является символом неопределенности и загадочности. Общепринятые математические методы не могут точно определить дальнейшую последовательность цифр числа pi. Более того, ученые до сих пор не смогли доказать, является ли число pi рациональным или иррациональным. Все это придает числу pi особую ценность и привлекательность для математиков и любителей науки по всему миру.
В целом, число пи – это одна из ключевых констант математики и науки в целом. Оно не только помогает в решении различных задач, но и является важнейшим символом загадочности и неопределенности, которые стимулируют ученых к поиску новых знаний и решению нетривиальных задач.






