Узнайте, что значит найти разность в математике, как это делается и какие методы решения применяются. Объяснение на простых примерах и пошаговые инструкции для быстрого понимания.
Математика – это наука, изучающая числа, их свойства и взаимоотношения. Основными операциями в математике являются сложение, вычитание, умножение и деление. Каждая из этих операций используется для решения конкретных задач. В данной статье мы рассмотрим операцию вычитания.
Вычитание – это операция нахождения разности двух чисел. Первое число называется уменьшаемым, а второе – вычитаемым. Разность двух чисел равна числу, которое нужно добавить к вычитаемому, чтобы получить уменьшаемое.
Например, если вычитаемое равно 5, а разность равна 3, то уменьшаемое будет равно 8. Формула для вычисления разности выглядит следующим образом: a – b = c, где a и b – числа, c – разность между ними.
Вычитание используется в различных областях знаний, включая физику, химию и экономику. Например, в экономике вычитание используется для расчета прибыли, а в физике – для вычисления скорости.
Теперь вы знаете, что такое найти разность в математике и как она используется в различных областях знаний. Для более глубокого понимания математики рекомендуется изучать не только отдельные операции, но и их взаимосвязь между собой.
Определение проверяемого понятия
При изучении математики различные понятия и концепции играют важную роль. Однако, для того чтобы студенты могли уверенно работать с математической теорией, им нужно понимать эти понятия и уметь их проверять.
Определение проверяемого понятия – это процесс, при котором студент выражает содержание понятия словами и символами в точном соответствии со смыслом, который ему был передан преподавателем. Это важно, чтобы удостовериться в том, что студенты понимают материал и могут работать с ним в своих задачах.
Обычно, определения проверяемого понятия содержат в себе теоретическое описание понятия, его свойства и атрибуты. Они часто включаются в учебники или прослушиваемые лекции, но могут также поставляться как дополнительный материал для работы с учащимися.
Также, для эффективной проверки понимания материала, преподаватели могут использовать различные методы и инструменты, такие как тесты, задания, упражнения и контрольные работы. Они могут помочь студентам проверить и закрепить свои знания, а также дать преподавателю обратную связь относительно того, что необходимо дополнительно объяснить или улучшить в своей методике обучения.
Определение проверяемого понятия – это неотъемлемая часть учебного процесса, которая помогает студентам освоить материал и научиться его применять в различных задачах и ситуациях.
Видео по теме:
Пояснение базовых понятий
Найти разность – одно из основных арифметических действий в математике, которое заключается в вычитании одного числа из другого. Результатом вычитания является число, равное разности вычитаемого числа и вычитателя.
Вычитаемое – число, которое вычитают из другого числа. Например, в операции 9 – 3, 9 является уменьшаемым, а 3 – вычитаемым.
Вычитатель – число, которое вычитывают из другого числа. В примере 9 – 3, 3 – вычитатель.
Разность – результат операции вычитания двух чисел. В нашем случае, 9 – 3 = 6, где 6 – разность.
Отрицательная разность – случай, когда вычитаемое число меньше вычитателя. Например, 3 – 9 = -6, где -6 – отрицательная разность.
Абсолютная величина разности – число, равное числу единиц в отрицательной разности. Другими словами, абсолютная величина разности – это модуль значения отрицательной разности. Например, абсолютная величина разности в примере 3 – 9 равна 6.
Что такое математическая разность
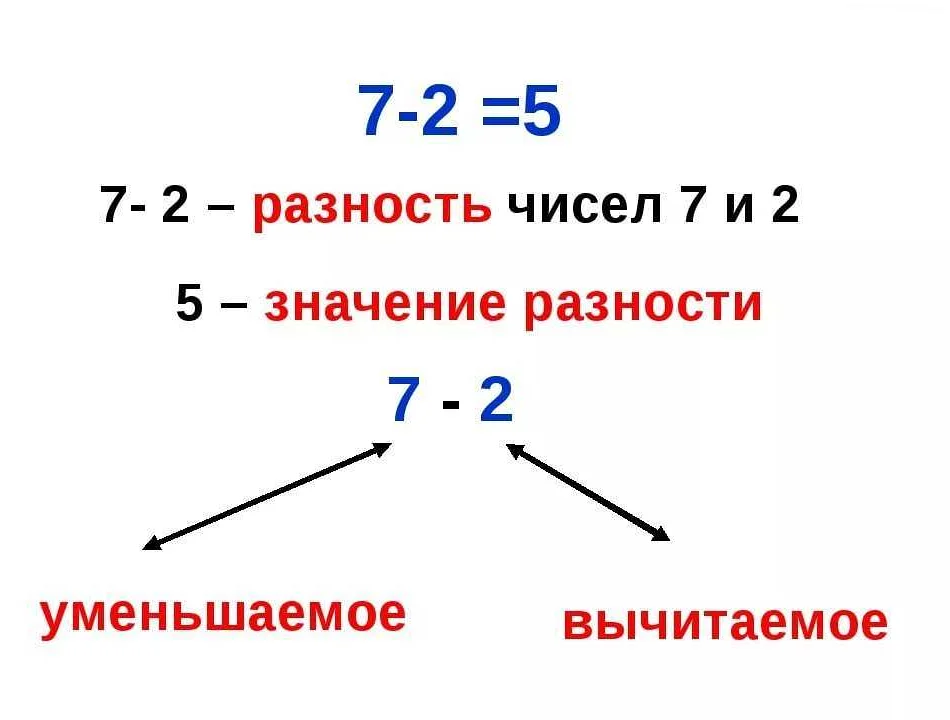
В математике под понятием “разность” понимается операция, которая предполагает вычитание одного числа из другого. Например, если у нас есть число 7, а мы вычитаем из него число 3, то получаем разность равную 4.
Математическую разность можно обозначить специальным знаком “-“, который применяется между вычитаемым и вычитателем. Если мы продолжим пример с числами 7 и 3, то математическая разность будет записана следующим образом: 7 – 3 = 4.
В зависимости от контекста, математическую разность можно использовать для решения различных задач. Например, при работе с графиками функций, математическая разность может быть использована для определения изменения значений функции в различных точках.
Стоит отметить, что математическая разность может применяться не только к целым числам, но и к числам с плавающей точкой (дробям). В таком случае, результат разности будет также являться числом с плавающей точкой.
Примеры и задачи на нахождение разности

Разность двух чисел определяется как результат вычитания одного числа из другого. Найти разность двух чисел можно с помощью обычного вычитания. Разность может быть положительной, отрицательной или равной нулю.
Пример 1: Найти разность 15 и 8.
Решение: 15 – 8 = 7. Разность равна 7.
Пример 2: Найти разность -10 и 5.
Решение: -10 – 5 = -15. Разность равна -15.
Пример 3: Найти разность 2 и 2.
Решение: 2 – 2 = 0. Разность равна 0.
Кроме того, можно решать задачи на нахождение разности с помощью таблицы вычитания или раскладывая числа на разряды.
Пример 4: Найти разность между 478 и 236.
| 4 | 7 | 8 |
| – | 2 | 3 |
| 2 | 5 | 5 |
Разность между 478 и 236 равна 242.
Пример 5: Найти разность между 999 и 333.
Решение: 999 – 333 = 666. Разность между 999 и 333 равна 666.
Задачи на нахождение разности в математике помогают развивать навыки вычитания и работать с числами.
Разность как одна из операций арифметики
Разность является одной из четырех основных операций арифметики. Она используется для вычисления разности между двумя числами. Операция вычитания может применяться как для целых чисел, так и для дробей.
При вычитании одного числа из другого, первое число называется уменьшаемым, а второе – вычитаемым. Разность двух чисел равна разнице между ними. Например, если массив яблок уменьшился на 3 штуки, а изначально в нем было 10 яблок, то разность будет равна 7.
Для вычисления разности двух чисел необходимо вычитаемое вычесть из уменьшаемого. Также возможно использование операции сложения. Например, чтобы вычислить разность 12 и 5, можно прибавить 5 к 7 и получить результат в виде 7. При этом будет использоваться операция противоположного действия, где вычитаемое превращается в прибавляемое.
Кроме того, существует понятие “абсолютной разности”, которое означает расстояние между двумя числами на числовой прямой. Она определяется как модуль разности между двумя числами. Например, абсолютная разность между 5 и -2 равна 7.
Сложение и вычитание: основная связь

Сложение и вычитание две основные операции в математике, которые часто используются в повседневной жизни. Они являются основой для всех других операций математики, таких как умножение и деление.
Сложение производится, когда мы хотим объединить два или более числа в одно число. Например, если у нас есть 2 яблока и мы добавляем еще 3 яблока, то мы можем сказать, что мы сложили 2 и 3, чтобы получить 5 яблок.
Вычитание, напротив, выполняется, когда мы хотим вычесть одно число из другого. Например, если у нас есть 5 яблок, а мы съели 2, то мы можем сказать, что мы вычли 2 из 5, чтобы получить 3 яблока, которые остались.
Основная связь между сложением и вычитанием заключается в том, что вычитание является обратной операцией к сложению. Это означает, что если мы знаем результат сложения двух чисел, мы можем вычесть одно из них, чтобы получить оставшееся число. Например, если мы имеем 2 и 3 яблока, то мы можем сложить их, чтобы получить 5. А затем, зная результат сложения, мы можем вычесть 2, чтобы получить 3, и вычесть 3, чтобы получить 2. Таким образом, связь между сложением и вычитанием является важной основой для всей математики.
Методы решения задач на разность
Разность – это операция вычитания одного числа из другого. Решение задач на разность часто требует использования особых методов, в зависимости от их сложности и типа.
Метод разбиения на промежутки: при работе с задачами, где нужно найти разность между двумя числами, которые находятся на разных промежутках, может быть полезно разбить эти промежутки на меньшие куски. Затем можно вычислить разность для каждого куска и составить окончательный результат. Например, если нужно найти разность между 30 и 55, можно разбить этот интервал на два промежутка: 30-40 и 41-55.
Метод пошагового упрощения: этот метод особенно полезен в случае, когда нужно найти разность, но оба числа имеют некоторые общие множители. В таком случае можно пошагово упрощать выражения, удаляя общие множители до тех пор, пока нельзя будет вычислить разность двух чисел. Например, если нужно найти разность между 72 и 48, можно сначала разделить каждое число на 12, чтобы получить 6 и 4, затем найти разность между ними.
Метод приведения к общему знаменателю: в случае, когда нужно найти разность между дробями, можно использовать метод приведения к общему знаменателю. Сначала нужно найти общий знаменатель для двух дробей, а затем привести каждую из них к этому знаменателю, чтобы можно было вычислить разность числителей. Например, для вычисления разности между 3/4 и 1/3 можно выбрать общий знаменатель 12 и привести обе дроби к этому знаменателю: 9/12 и 4/12. Затем можно вычислить разность числителей: 9/12 – 4/12 = 5/12.
Метод использования похожих треугольников: этот метод полезен при решении геометрических задач на нахождение разности расстояний, высот или сторон между двумя треугольниками. Идея заключается в том, чтобы использовать сходство двух треугольников и пропорциональность сторон. Например, если нужно найти разность между высотами двух подобных треугольников, можно использовать пропорцию высот к соответствующим сторонам этих треугольников.
Это не полный список методов, но они помогают решать большинство задач, связанных с операцией разности.
Обзор других математических понятий в контексте разности
Разность в математике используется для определения различий между двумя числами. Знак “-” используется для обозначения разности.
Другим математическим понятием, которое связано с разностью, является сумма. Сумма в математике используется для объединения двух или более чисел и обозначается знаком “+”. Разность и сумма являются инверсиями друг друга.
Также в контексте разности важным понятием является абсолютная величина. Абсолютная величина числа – это числовое значение без учета его знака. Например, абсолютная величина -10 равна 10, а абсолютная величина 5 также равна 5.
Другое понятие, которое также связано с разностью, – это расстояние. Расстояние между двумя точками может быть найдено путем вычисления абсолютной величины разности их координат. Например, расстояние между точками (3,4) и (7,9) равно 6.403.
В некоторых случаях, можно использовать таблицу для демонстрации разности. Таблица может помочь при вычислении большого количества чисел и демонстрации их разности.
- Разность большего числа и меньшего числа является положительным числом
- Для двух одинаковых чисел разность равна нулю
- Разность двух положительных чисел может быть отрицательна
В общем, можно заметить, что существует много математических понятий, связанных с разностью. За их пониманием могут следовать лучшее понимание темы в целом и вычисления, связанные с разностью, могут быть проще выполнены.
Разность и аналогичные алгебраические выражения
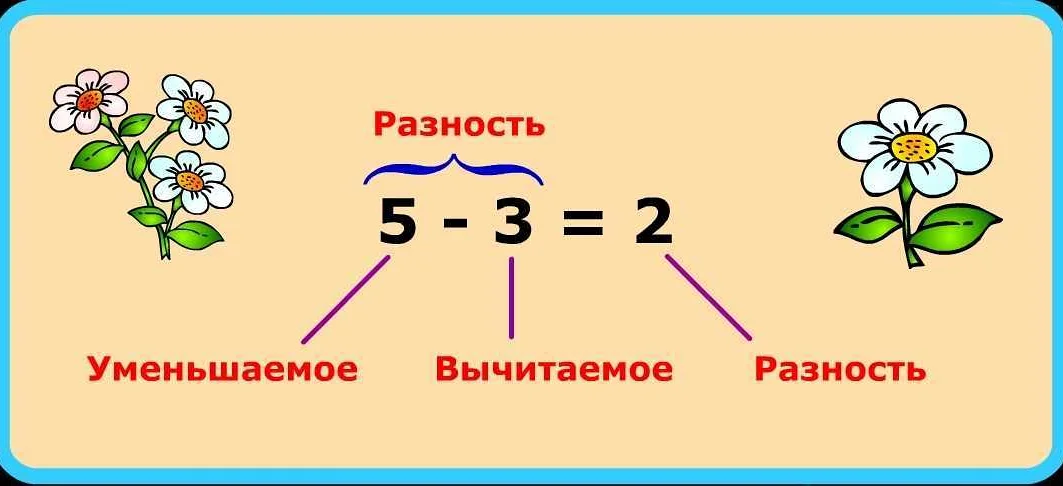
Разность – это алгебраическое выражение, обозначающее разницу между двумя числами или переменными. Символ “–” используется для обозначения разности.
Например: разность 10 и 5 обозначается как 10 – 5 = 5.
Другие алгебраические выражения, которые могут быть аналогичны разности, это сумма, произведение и частное.
- Сумма обозначается символом “+”. Например, 10 + 5 = 15.
- Произведение обозначается символом “*”. Например, 10 * 5 = 50.
- Частное обозначается символом “/”. Например, 10 / 5 = 2.
Важно помнить, что порядок операций в алгебраических выражениях также имеет значение.
Алгебраическое выражениеРезультат
| 10 + 5 * 2 | 20 |
| (10 + 5) * 2 | 30 |
В первом примере, сначала выполняется умножение 5 на 2, а затем сложение результата с 10, что даёт 20. Во втором примере, сначала выполняется сложение 10 и 5, затем умножение результата на 2, что даёт 30.
Вопрос-ответ:
Как найти разность двух чисел?
Для этого нужно вычитать из большего числа меньшее. Например, если нам нужно найти разность 10 и 5, то 10-5=5.
Как найти разность дробей?
Для этого нужно вычитать числитель и знаменатель каждой дроби. Затем результаты упрощаются до минимального вида, если это возможно.
Как найти абсолютную разность?
Абсолютная разность – это разность чисел по модулю. Для этого нужно вычислить разность, а затем взять модуль полученного числа.
Как использовать разность в математическом анализе?
Разность используется в математическом анализе для нахождения порядка изменения функции, например, производной. Для этого вычисляют разность функции между двумя близкими точками и делят ее на расстояние между этими точками.
Как применить понятие разности в статистике?
Разность может быть использована в статистике для определения изменения между двумя наборами данных. Например, для определения изменений за определенный период времени можно вычислить разность между средними значениями двух наборов данных.
Какая формула для вычисления разности квадратов?
Формула для разности квадратов: (а-b)(a+b)=a²-b². Эта формула может быть использована, например, для факторизации полиномов.
Как использовать разность в теории вероятности?
В теории вероятности разность может быть использована для расчета вероятности событий, которые не являются независимыми. Например, вероятность того, что событие А произойдет, если произошло событие В, может быть вычислена как вероятность события А минус вероятность событий А и В.






