Статья рассказывает о понятии стороны в математике, о ее определении и свойствах. Рассмотрены различные типы сторон в геометрии и их применение в расчетах и задачах.
Математика – это наука о количественных отношениях и изучении их свойств. Одним из основных понятий в математике является понятие “сторона”. Сторона – это одна из линий, образующих геометрическую фигуру. Она является непосредственной визуальной составляющей для определения формы фигуры и ее свойств.
Концепция стороны применяется в различных областях математики: геометрии, тригонометрии, алгебре, анализе и других. Изучая эти области, мы узнаем, какие основные понятия и операции используются в математике и как они могут быть применены на практике.
Организация и определение стороны в различных фигурах имеет свои особенности. Например, в треугольнике три стороны, в квадрате – четыре, а в круге – единственная. Знание основных понятий в математике, таких как сторона, облегчает понимание более сложных математических концепций в будущем, и подготавливает нас к работе в науке и технологии.
Сторона – определение и общие понятия
Сторона – это одно из основных понятий геометрии, которое обозначает любую из линий, ограничивающих геометрическую фигуру (например, треугольник или квадрат) или угол.
Сторона измеряется длиной и может быть горизонтальной, вертикальной или диагональной. Геометрическая фигура может иметь разное количество сторон, например, треугольник имеет три стороны, а пятиугольник – пять.
Каждая сторона геометрической фигуры имеет свои свойства и характеристики. Например, стороны треугольника могут быть равными или неравными, прямыми или кривыми, острыми или тупыми. В зависимости от свойств сторон, можно определить некоторые характеристики самой фигуры, например, её периметр и площадь.
Изучение свойств сторон и геометрических фигур играет важную роль в математике, а также имеет множество практических применений в различных областях деятельности, например, в архитектуре, инженерии, дизайне и технологии.
Какие бывают стороны в геометрии
Страница – это линия, ограничивающая фигуру или многогранник в геометрии. Стороны могут быть различными по длине, форме и углам. Существует несколько видов сторон в геометрии, вот некоторые из них:
- Равные стороны: это стороны с одинаковой длиной. Например, квадрат имеет четыре равные стороны.
- Перпендикулярные стороны: это стороны, которые встречаются под прямым углом. Например, в прямоугольнике каждая пара соседних сторон перпендикулярна.
- Параллельные стороны: это стороны, которые никогда не пересекаются. Например, у параллелограмма две пары параллельных сторон.
- Противоположные стороны: это пара сторон, которые находятся друг против друга в фигуре. Например, у прямоугольника противоположные стороны равны и параллельны.
Знание типов сторон может помочь в решении геометрических задач и строительных проектов. Кроме того, определение сторон является важной составляющей в изучении геометрии.
Стороны треугольника и их свойства
Треугольник – это геометрическая фигура, состоящая из трех сторон и трех углов. Основные свойства треугольника связаны именно со сторонами.
Первое свойство – сумма длин любых двух сторон треугольника всегда больше длины третьей стороны. Если даны длины двух сторон, то третья может быть найдена по формуле: a + b > c.
Второе свойство – стороны треугольника могут быть равными или разными. Треугольник, у которого все три стороны равны, называется равносторонним. Если две стороны равны, то треугольник называется равнобедренным. Если все стороны разные, то треугольник называется разносторонним.
Третье свойство – каждая сторона треугольника имеет противолежащий угол. Таким образом, треугольник состоит из трех углов и трех сторон, каждая из которых противолежит соответствующему углу.
Четвертое свойство – сторона treugol’nika, находящаяся между двумя острыми углами, больше, чем сторона против меньшего из этих углов. Если угол прямой, то две катеты (стороны, прилегающие к прямому углу) являются противолежащими сторонами для этого угла, а гипотенуза (стоница напротив прямого угла) является наименьшей стороной треугольника. Можно использовать теорему Пифагора, чтобы найти длину гипотенузы, a^2 + b^2 = c^2.
Пятый факт – угол треугольника всегда меньше суммы углов в полном круге, который равен 360 градусов. Получается, что сумма всех трех углов треугольника равна 180 градусам. Если один из углов равен 90 градусов, то два других могут быть найдены по формуле 90 + x + y = 180, где x и y – два других угла.
Стороны многоугольника и их свойства
Многоугольник – геометрическая фигура, которая имеет три или более сторон, ограниченных прямыми линиями.
В многоугольнике каждая из сторон является отрезком, соединяющим две соседние вершины. Стороны многоугольника имеют несколько свойств:
- Длины сторон многоугольника могут быть равными или разными.
- Все стороны многоугольника лежат в одной плоскости.
- Длины сторон многоугольника могут быть равны отрезкам, соединяющим вершины фигуры.
- Сумма длин всех сторон многоугольника является периметром многоугольника.
Также стороны многоугольника могут быть классифицированы по форме многоугольника:
- Равносторонний многоугольник имеет все стороны равными.
- Разносторонний многоугольник имеет разные длины сторон.
- Равнобедренный многоугольник имеет хотя бы две равные стороны.
- Прямоугольный многоугольник имеет одну прямой угол и пары противоположных сторон равны.
Знание свойств сторон многоугольника необходимо при решении задач на вычисление площади, периметра или измерении углов фигуры.
Стороны круга и касательные
Круг – это геометрическая фигура, которая состоит из всех точек плоскости, находящихся на определенном расстоянии от центра. В круге есть несколько характеристик и параметров, среди которых касательные и стороны.
Строго говоря, в круге нет сторон. Однако, существует понятие радиуса, который является отрезком, соединяющим центр круга и любую точку его окружности. Радиус – это одна из возможных мер для определения расстояния между центром и точками на окружности, но не сторона.
Касательная – это прямая, которая касается окружности в одной точке. Каждая касательная имеет только одну точку касания с окружностью. Кроме того, касательная в этой точке перпендикулярна радиусу, проходящему через эту точку. От точки касания касательная является секущей линией окружности.
Важно помнить, что в круге, как и в любой геометрической фигуре, каждый элемент имеет свои характеристики и свойства. Стороны в круге отсутствуют, но есть радиусы и касательные. Эти элементы могут быть использованы для вычисления различных параметров круга и решения задач на геометрию.
Стороны в пространственных фигурах
Пространственные фигуры имеют более сложную структуру, чем плоские. Они состоят из граней, в которых каждая грань состоит из ребер.
Стороны в пространственных фигурах носят название ребер. Ребро – это отрезок, соединяющий две вершины, которое образует грань пространственной фигуры. Ребра являются базовыми элементами любой пространственной фигуры.
Стороны пространственных фигур могут иметь разную форму, длину и направление. Например, в пирамиде все боковые стороны соединяются в одну общую вершину, а нижняя сторона является основанием пирамиды. В кубе все стороны равны и перпендикулярны друг другу, тогда как в призме стороны могут быть различными.
Если ребра имеют одинаковую длину и все грани замкнуты, то такая фигура называется правильной. К примеру, октаэдр имеет 8 правильных треугольников в качестве граней и 12 ребер, которые соединяют эти грани.
Стороны пространственных фигур играют важную роль в геометрических вычислениях и в повседневной жизни. Понимание различных форм и свойств сторон помогает в построении и измерении объектов, а также в решении различных задач в пространстве.
Длина стороны – формула и способы вычисления
Длина стороны является одним из основных параметров геометрических фигур, таких как прямоугольник, квадрат, треугольник и другие. При работе с этими фигурами необходимо знать, как вычислять длину их сторон. Существует несколько способов вычисления длины сторон в зависимости от вида фигуры.
Для вычисления длины стороны квадрата формула будет выглядеть следующим образом: s = a, где s – длина стороны, а a – длина стороны квадрата. То есть, длина всех четырех сторон квадрата одинакова.
Для вычисления длины сторон прямоугольника формула будет иметь вид: s = 2(a + b), где a и b – длины двух противоположных сторон прямоугольника. Данная формула позволяет вычислить длину всех четырех сторон этой геометрической фигуры.
Для вычисления длины сторон треугольника используются различные формулы, в зависимости от известных параметров. Например, для правильного треугольника формула будет выглядеть следующим образом: s = a√3, где a – длина стороны треугольника. Если известна высота треугольника, можно использовать формулу: s = 2ah, где a – длина основания треугольника, а h – его высота.
- Для вычисления длины стороны квадрата используется формула: s = a.
- Для вычисления длины сторон прямоугольника применяется формула: s = 2(a + b).
- Для вычисления длины сторон треугольника используются различные формулы, в зависимости от известных параметров.
Таким образом, значение длины сторон является важным параметром для работы с различными геометрическими фигурами, а знание формул и способов вычисления позволяет более грамотно проводить расчеты и строить фигуры.
Сверление сторон и проверка равенства сторон

В математике стороной называется отрезок, соединяющий две вершины фигуры. Каждая фигура имеет определенное количество сторон, которые могут быть разной длины.
Чтобы проверить, являются ли все стороны фигуры равными, необходимо измерить каждую сторону при помощи линейки или известной математической формулы. Если длина всех сторон одинакова, то скорее всего фигура является правильной.
В случае, если две стороны фигуры имеют разную длину, можно применить метод сверления сторон. Для этого необходимо поместить конец линейки на одну из сторон, а затем продолжить движение линейки по другой стороне фигуры до тех пор, пока не будет достигнут конец. Таким образом, можно сравнить длину двух или более сторон и получить информацию об их равенстве или несоответствии.
Проверка равенства сторон является важным элементом геометрии и используется в различных областях, таких как проектирование зданий, строительство дорог и мостов, а также в изучении геометрии на разных уровнях обучения.
Стороны и гипотенуза: теорема Пифагора
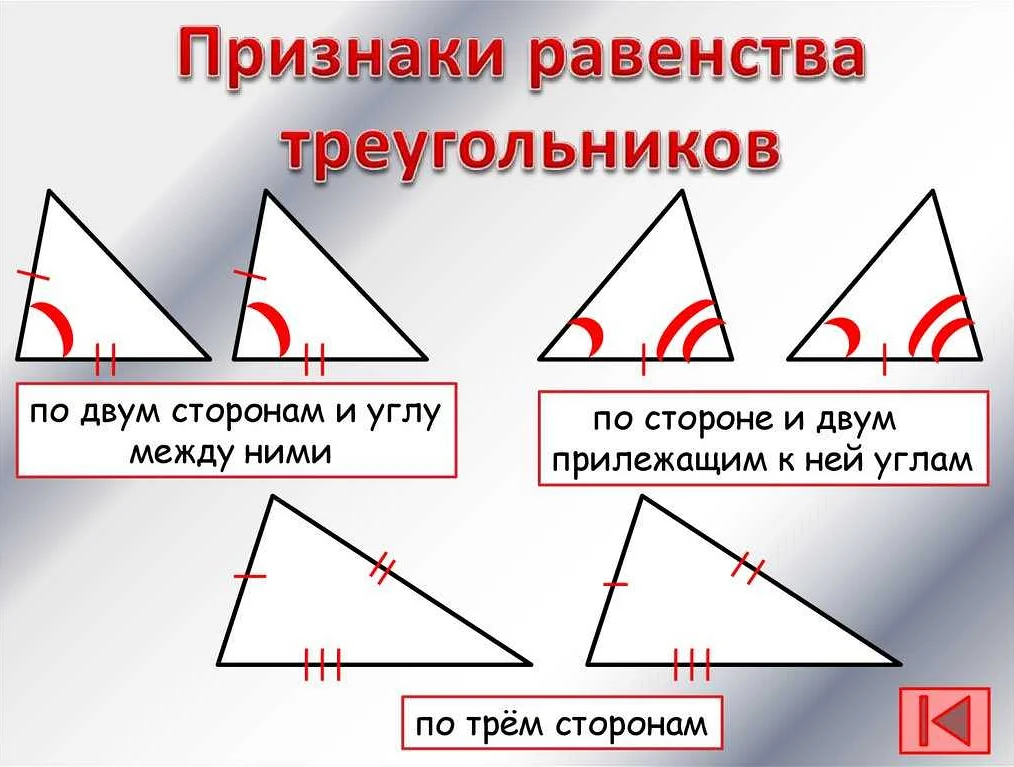
Теорема Пифагора – основополагающая теорема геометрии, которая устанавливает связь между длинами сторон прямоугольного треугольника. Согласно этой теореме, квадрат длины гипотенузы прямоугольного треугольника равен сумме квадратов длин катетов.
Для обозначений длин сторон прямоугольного треугольника используют буквы a, b и c. Соответственно, гипотенуза обозначается буквой c, а каждый из катетов – буквой a или b.
Формула теоремы Пифагора выглядит следующим образом:
c2 = a2 + b2
Эта формула позволяет рассчитать длину гипотенузы, если известны длины катетов, или наоборот – длину одного из катетов, если известны длины гипотенузы и другого катета.
Применение теоремы Пифагора широко распространено в геометрии, физике, астрономии и других областях науки. К примеру, на основе этой теоремы можно рассчитать длину телескопической антенны, определить расстояние между звездами или найти длину диагонали экрана телевизора.
Вопрос-ответ:
Что такое сторона в математике?
В математике сторона – это любой отрезок, соединяющий две вершины геометрической фигуры. Например, в прямоугольнике стороны – это две отрезка, соединяющие противоположные вершины. В треугольнике – это три отрезка, соединяющие вершины треугольника. В круге сторон нет, так как круг не имеет вершин.
Как найти длину стороны?
Для нахождения длины стороны необходимо знать координаты ее конечных точек и воспользоваться формулой расстояния между двумя точками на плоскости: d = sqrt((x2-x1)^2 + (y2-y1)^2), где (x1,y1) и (x2,y2) – координаты конечных точек стороны.
Какие бывают виды сторон?
Виды сторон зависят от геометрической фигуры. Например, в круге сторон нет, в треугольнике – три стороны, в квадрате – четыре стороны, в правильном пятиугольнике – пять сторон и т.д.
Что такое гипотенуза?
Гипотенуза – это самая длинная сторона прямоугольного треугольника, которая находится напротив прямого угла. Она вычисляется по теореме Пифагора: c^2 = a^2 + b^2, где c – гипотенуза, a и b – длины катетов (двух других сторон, которые лежат при прямом угле).
Как определить, является ли сторона равнобедренной?
Строится биссектриса угла, образованного двумя данными сторонами. Если биссектриса является одновременно и медианой, то данная сторона является равнобедренной. То есть она равна по длине другой стороне, образующей данный угол.
Как определить, является ли сторона подобной?
Для того чтобы определить, является ли сторона подобной, необходимо сравнить ее со всеми другими сторонами данной геометрической фигуры. Если соотношение длин всех соответствующих сторон одинаково, то фигуры подобны, а их стороны пропорциональны. Например, если соотношение длин сторон одного треугольника равно 2:3:4, то соотношение длин сторон другого подобного треугольника также будет равно 2:3:4.
Какие свойства имеют параллельные стороны?
Параллельные стороны имеют следующие свойства: они лежат на одной плоскости, никогда не пересекаются, имеют равные длины и равные углы между параллельными сторонами. Если две прямые параллельны, то углы, образованные при пересечении этих прямых со сторонами, равны между собой.
Как использовать знание о сторонах в решении задач по математике
Знание о сторонах полезно для решения задач по геометрии и тригонометрии. Например, в треугольниках можно использовать теорему Пифагора, которая связывает длины сторон треугольника.
Также, знание о сторонах может помочь расчетать площадь фигуры. Например, для прямоугольника площадь равна произведению двух сторон, для квадрата площадь равна квадрату длины стороны.
В тригонометрии знание о сторонах необходимо для вычисления тригонометрических функций. Например, для нахождения синуса или косинуса угла в прямоугольном треугольнике нужно знать длины двух сторон.
В некоторых задачах также необходимо знать, какие стороны являются гипотенузой или катетами прямоугольного треугольника. Это позволяет определить, какие тригонометрические функции нужно использовать в расчетах.
Итак, знание о сторонах является важным элементом при решении задач по математике. Правильное использование этого знания может помочь значительно ускорить процесс решения задач и добиться точных результатов.






