Статья рассказывает о динамике колебаний математического маятника: как она описывается уравнением, как изменяются амплитуда и период колебаний при разных условиях, в том числе с учетом сопротивления среды. Подробный анализ позволяет понять, какие факторы влияют на колебательную систему и какие законы управляют ее работой.
Математический маятник представляет собой идеализированную модель, которая очень полезна для анализа и понимания различных колебательных процессов.
Один из главных аспектов динамики колебаний математического маятника – это понятие собственного периода колебаний. Он определяется геометрическими параметрами маятника (длина подвеса, масса шарика) и не зависит от начальной амплитуды колебаний. Также важно понимать, что период колебаний является инертным свойством самого маятника и не зависит от внешних факторов (например, силы трения).
Однако, кроме собственного периода колебаний, математический маятник может испытывать внешнее воздействие, которое будет изменять его движение. Именно это исследуется в динамике колебаний математического маятника – как различные факторы (например, сила тяжести, сопротивление воздуха, дополнительные массы) влияют на движение маятника и как можно описать это движение математически.
Определение колебаний
Колебания – это движение, при котором тело перемещается сначала в одну сторону, а затем – в другую. Движение осуществляется вокруг некоторого положения равновесия, к которому тело стремится вернуться, когда на него не действуют внешние силы.
Колебания могут быть регулярными и нерегулярными. Регулярные колебания имеют постоянный период и амплитуду, образующие друг с другом определенный закон. Нерегулярные колебания, напротив, имеют непостоянный период и амплитуду.
Колебания в природе могут возникать из-за различных факторов – например, из-за передачи энергии от одного тела к другому, из-за изменения равновесного положения системы или из-за возбуждения некоторого резонанса в системе.
- В качестве примера колебаний можно привести колебания математического маятника, при которых маятник переходит из движения в одну сторону в движение в другую сторону.
- Еще одним примером можно назвать колебания пружинного маятника, при котором движение происходит вдоль оси пружины.
Важно отметить, что колебания широко используются в науке и технике, и их изучение позволяет создавать различные средства и устройства – например, такие как кварцевые часы или инерционные навигационные системы.
Видео по теме:
Описание математического маятника
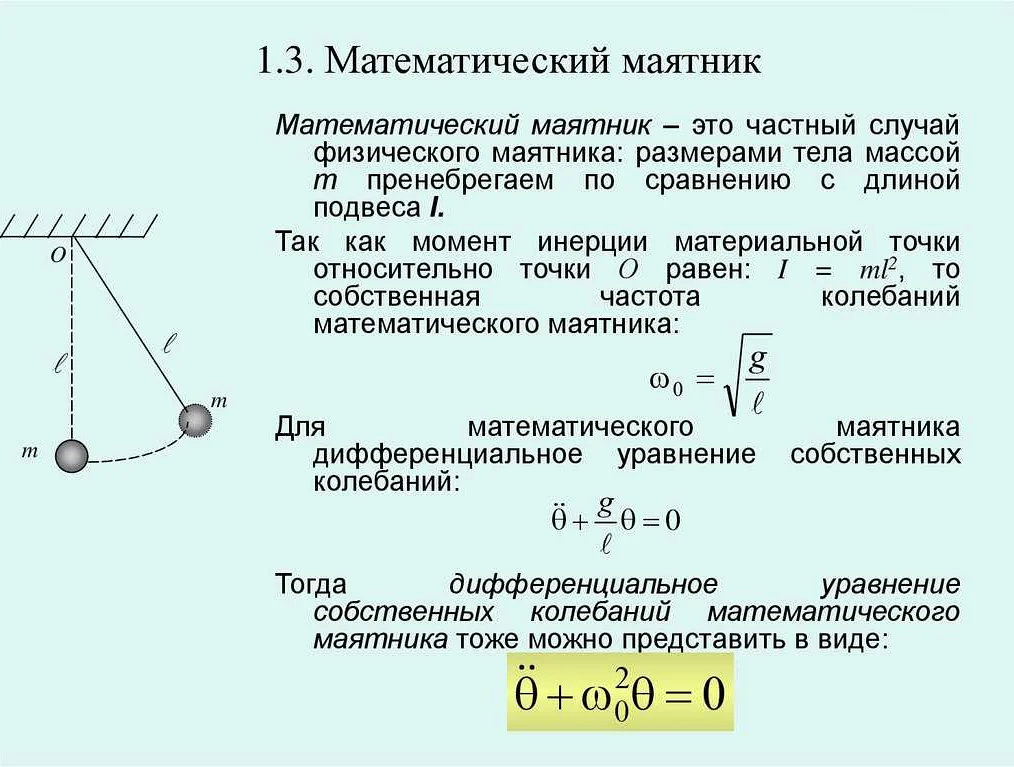
Математический маятник – это физическая система, которую можно описать математически с помощью уравнений движения. Он состоит из точечной массы, подвешенной на невесомом и нерастяжимом стержне. Математический маятник является одним из простейших механических колебательных систем и широко используется в научных и практических областях.
Для описания движения математического маятника используется уравнение гармонических колебаний. Это уравнение описывает движение маятника при условии, что его колебания не диссипируются, то есть система не теряет энергию.
Уравнение гармонических колебаний выглядит следующим образом: x = A*cos(ωt + φ), где x – отклонение точечной массы, А – амплитуда колебаний, ω – частота колебаний, t – время, а φ – начальная фаза колебаний. Частота колебаний зависит от длины стержня и ускорения свободного падения, а начальная фаза колебаний зависит от начальных условий.
Математический маятник является важным инструментом для изучения динамики колебаний и применяется в различных научных областях, включая физику, математику и инженерное дело.
Формулы и характеристики колебаний
Для описания колебаний математического маятника применяются формулы, которые связывают его период, частоту и амплитуду колебаний.
Период колебаний (T) математического маятника выражается формулой:
T = 2π√(l/g)
где l – длина подвеса маятника, а g – ускорение свободного падения.
Частота колебаний (f) определяется как обратная величина периода:
f = 1/T
Амплитуда колебаний (A) – это максимальное отклонение маятника от положения равновесия, которое зависит от начальных условий. Определяется формулой:
A = lθ
где θ – угол отклонения маятника от положения равновесия.
Важной характеристикой колебаний является декремент затухания (δ), который обозначает скорость уменьшения амплитуды колебаний во времени:
δ = (ln(An/An+1))/(2π)
где An и An+1 – амплитуды двух последовательных колебаний.
Другой характеристикой колебаний является логарифмический декремент (Λ), который определяется как отношение декремента затухания к числу колебаний:
Λ = δ/n
где n – число колебаний.
В таблице ниже приведены значения формул и характеристик колебаний для математического маятника:
ВеличинаФормулаЗначение
| Период колебаний | T = 2π√(l/g) | Зависит от длины подвеса и ускорения свободного падения |
| Частота колебаний | f = 1/T | Обратная величина периода |
| Амплитуда колебаний | A = lθ | Максимальное отклонение маятника от положения равновесия |
| Декремент затухания | δ = (ln(An/An+1))/(2π) | Скорость уменьшения амплитуды колебаний во времени |
| Логарифмический декремент | Λ = δ/n | Отношение декремента затухания к числу колебаний |
Уравнение движения математического маятника
Математический маятник – это простейшая модель, которая позволяет описать колебания твердого тела вокруг определенной точки. Уравнение движения математического маятника описывает его колебания и можно записать в виде:
T = 2π√(L/g),
где T – период колебаний маятника, L – длина подвеса маятника, g – ускорение свободного падения.
Уравнение показывает, что период колебаний математического маятника не зависит от его массы и амплитуды, а зависит только от длины подвеса и ускорения свободного падения.
Важно учитывать, что уравнение движения математического маятника является идеализированной моделью, которая не учитывает внешние факторы, такие как сопротивление воздуха и трение. Эти факторы могут влиять на период колебаний математического маятника и делают его движение более сложным.
Таким образом, уравнение движения математического маятника является важным инструментом для понимания динамики колебаний твердых тел, включая системы с большим числом степеней свободы.
Режимы колебаний математического маятника
Математический маятник – это система, которая колеблется вокруг неподвижной точки под воздействием силы тяжести. Как и любая колебательная система, маятник может находиться в различных режимах колебаний.
Один из основных режимов колебаний – это критический режим. В этом режиме период колебаний маятника равен периоду его малых колебаний, а амплитуда колебаний уменьшается во времени, что приводит к затуханию колебаний.
Еще один режим – это свободные колебания. В этом режиме колебания маятника не подвергаются никакому внешнему воздействию и происходят только под действием силы тяжести. Свободные колебания являются чисто гармоническими и продолжаются бесконечно долго, если не нарушить условия колебаний.
Также, существует режим вынужденных колебаний, при котором маятник подвергается внешнему воздействию с периодом, отличным от его естественного периода колебаний. В этом случае амплитуда колебаний может быть как больше, так и меньше, чем в свободных колебаниях, и зависит от соотношения естественного периода колебаний маятника и периода внешней силы.
Важно отметить, что переход маятника из одного режима колебаний в другой может происходить за счет изменения параметров системы или под действием внешних воздействий.
Период колебаний математического маятника
Период колебаний математического маятника – это время, за которое маятник проходит один полный цикл. Он зависит только от длины маятника и ускорения свободного падения.
Формула для периода колебаний математического маятника имеет вид:
T=2π√(l/g)
Здесь Т – период колебания, π – число пи (примерно 3,14), l – длина маятника, g – ускорение свободного падения.
Из формулы видно, что период колебаний математического маятника не зависит от массы маятника, а только от длины и ускорения свободного падения.
Значение периода колебаний математического маятника можно использовать для решения различных задач, например, для определения ускорения свободного падения по периоду колебаний маятника.
Амплитуда колебаний математического маятника
Амплитуда колебаний математического маятника – это максимальное отклонение маятника от положения равновесия во время колебаний. В математическом смысле, амплитуда представляет собой абсолютное значение разности между положением равновесия и крайней точкой колебаний.
Закон сохранения энергии, описывающий колебания математического маятника, утверждает, что энергия колебаний сохраняется и переходит из кинетической в потенциальную форму и наоборот. Амплитуда колебаний математического маятника напрямую связана с его энергией.
Увеличение амплитуды колебаний, как и увеличение энергии маятника, приводит к увеличению скорости падения маятника и, как следствие, к увеличению угла отклонения от положения равновесия. Однако, есть пределы амплитуды колебаний, которые не могут быть превышены. Эти пределы связаны с физическими свойствами механизма маятника и энергетическим равновесием.
Фазовый угол колебаний математического маятника
Фазовый угол – это угол между началом координат и точкой, которая описывает колебания гармонического осциллятора на фазовой плоскости. В контексте математического маятника, фазовый угол определяет момент времени в колебательном процессе.
Фаза колебаний характеризуется расстоянием на фазовой плоскости между точкой, соответствующей начальному моменту времени, и точкой, соответствующей текущему моменту времени. Фазовый угол определяется как арктангенс от соотношения амплитуды и скорости колебательного движения.
Вклад фазового угла в динамику колебаний математического маятника определяется в основном тем, как фазовый угол изменяется с течением времени. Изменения фазового угла могут быть спонтанными или вызванными внешними возмущениями, такими как трение, сила сопротивления воздуха или другие причины.
Фазовый угол математического маятника может быть выражен через смещение и скорость колебаний, что позволяет установить связь между угловыми позициями и угловыми скоростями. Это свойство фазового угла может быть использовано для математического описания движения маятника и его динамических свойств.
Энергия колебаний математического маятника
Колебания математического маятника происходят за счет перехода энергии потенциальной в кинетическую и обратно. В крайних точках движения, в точке наивысшего подъема и в точке наименьшего подъема, энергия маятника полностью представлена потенциальной формой. В точке равновесия находится наименьшая потенциальная энергия маятника.
При движении маятника, потенциальная энергия в точке наибольшего подъема полностью переходит в кинетическую энергию в точке прохождения через точку равновесия. На возвращающем пути к точке наибольшего подъема маятник снова обладает лишь потенциальной энергией. В точках максимального отклонения от положения равновесия, все энергии маятника потенциальная.
Таким образом, энергия колебаний математического маятника не только сохраняется в циклическом движении, но и переходит из одной формы в другую, а также обратно.
Математический маятник – простейший вид колебательной системы, на котором можно проиллюстрировать законы сохранения и перехода энергии.
Измерение колебаний математического маятника
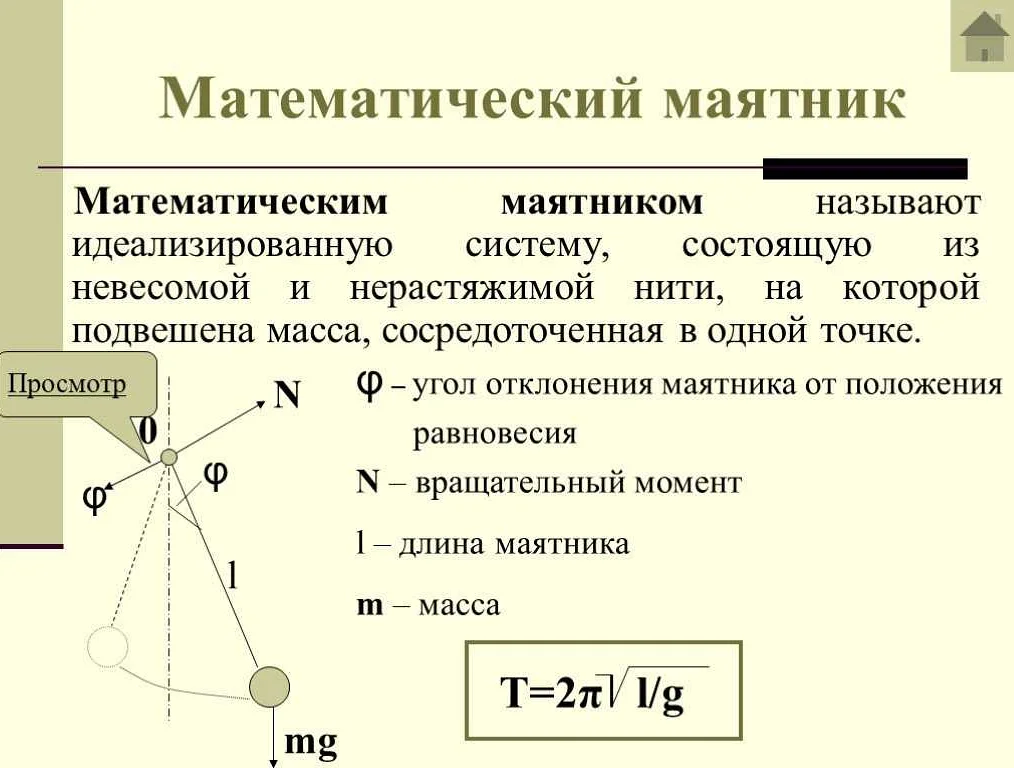
Для измерения колебаний математического маятника используются специальные инструменты. Одним из наиболее распространенных инструментов является таймер. Он позволяет засекать время колебаний маятника и определить период. Также используется линейка или мерная лента для измерения амплитуды колебаний.
Процесс измерения колебаний математического маятника может быть упрощен с помощью компьютера и программного обеспечения, которые позволяют засекать время колебаний и строить графики зависимости параметров колебаний от времени.
Для уменьшения погрешности измерений и получения более точных результатов важно использовать инструменты правильно. Необходимо установить маятник в точном положении и провести несколько измерений для усреднения полученных значений.
Измерение колебаний математического маятника является важной частью исследования динамики колебаний. Оно позволяет получить данные об основных параметрах колебаний и изучить их свойства и закономерности.
Вопрос-ответ:
Какова формула для вычисления периода колебаний математического маятника?
Формула для вычисления периода колебаний математического маятника: T = 2π√(l/g), где l – длина маятника, g – ускорение свободного падения.
Как зависит период колебаний математического маятника от его длины?
Период колебаний математического маятника пропорционален квадратному корню из длины маятника. То есть, чем длиннее маятник, тем дольше его период колебаний.
Можно ли изменить период колебаний математического маятника?
Да, период колебаний математического маятника можно изменить, например, изменив его длину или массу.
Что происходит с периодом колебаний математического маятника при изменении его массы?
Период колебаний математического маятника не зависит от его массы. Это свойство математического маятника называется изохронизмом.
В чем заключается динамика колебаний математического маятника?
Динамика колебаний математического маятника состоит в том, что при отклонении маятника от положения равновесия возникает кинетическая и потенциальная энергия, которые сменяют друг друга в процессе колебаний.
Какова связь между периодом колебаний математического маятника и его кинетической и потенциальной энергией?
Период колебаний математического маятника зависит от ее длины и ускорения свободного падения. Кинетическая энергия маятника возрастает при отклонении от положения равновесия и достигает максимума в момент прохождения центрального положения, а потенциальная энергия убывает до нуля в этот момент. Затем потенциальная энергия возрастает до максимума, когда маятник достигает крайней точки отклонения, а кинетическая энергия убывает до нуля в этот момент. Таким образом, период колебаний математического маятника связан с периодом колебаний его потенциальной и кинетической энергии.
Как влияет на период колебаний математического маятника силовое воздействие?
Период колебаний математического маятника зависит от силовых воздействий на него. Если на маятник действует дополнительная сила, то его период колебаний может измениться.






