Понятно о факториале в математике. Узнайте, что такое факториал, как его вычислить и примеры применения в простых словах.
Факториал – это одна из основных математических операций, которая определяет произведение всех натуральных чисел от 1 до заданного числа n. Факториал обычно обозначается символом ! и записывается после числа.
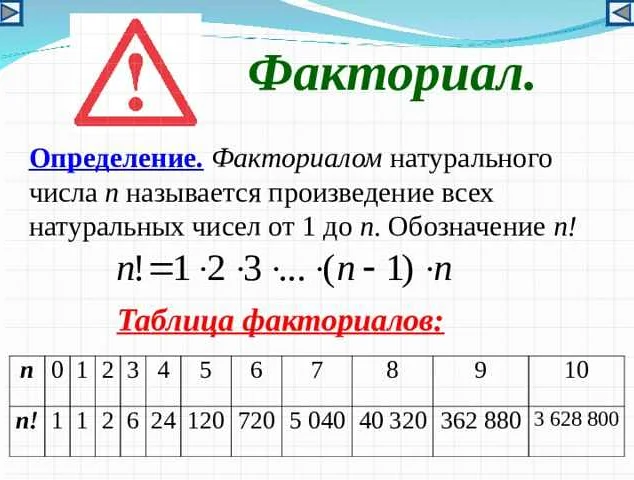
Например, факториал числа 5 вычисляется так: 5! = 5 * 4 * 3 * 2 * 1 = 120. А факториал числа 10 равен: 10! = 10 * 9 * 8 * 7 * 6 * 5 * 4 * 3 * 2 * 1 = 3628800.
Факториалы часто используются в математике и других науках, таких как статистика и теория вероятности. Например, для вычисления количества возможных перестановок объектов используется факториал числа элементов.
Понимание факториала – это важный элемент базовых математических знаний, который может пригодиться в жизни в различных областях. Существуют различные методы вычисления факториала, но основная идея остается неизменной – умножение всех натуральных чисел от 1 до n.
Факториал в математике
Факториалом натурального числа называется произведение всех натуральных чисел от 1 до этого числа включительно. Факториал обозначается восклицательным знаком и записывается после числа, например, 5!, что равно 1*2*3*4*5=120.
Факториал используется в различных задачах комбинаторики, вероятности и теории чисел. Например, для вычисления количества перестановок элементов множества используется факториал. Если множество A содержит n элементов, то число перестановок этого множества равно n!.
Также факториал используется при решении задач на вычисление вероятностей в схемах со случайными событиями. Например, если у нас имеется множество из n элементов и мы выбираем из него k элементов, то количество способов выбрать k элементов равно n!/(k!(n-k)!), где k!(n-k)! обозначает произведение факториалов этих чисел.
В математической нотации факториал можно представить с помощью гамма-функции Г, равной произведению всех целых чисел от 1 до n-1. Тогда n! = Г(n+1).
Видео по теме:
Определение
Факториал – это математическое понятие, обозначаемое символом “!”. Если натуральное число “n” больше нуля, то факториал n обозначает произведение всех натуральных чисел от 1 до n включительно.
То есть, n! = 1 * 2 * 3 * … * n.
Значение факториала является целым числом и может быть представлено в виде большой цифровой последовательности, так как результат может быть очень большим. Например, 10! = 3 628 800.
Факториалы используются в комбинаторике, теории вероятности, статистике и других областях математики. Они также часто встречаются в простых задачах на формирование различных комбинаций или вариантов.
Например, определить количество вариантов расстановки 6 шахматных фигур на шахматной доске (считая, что фигуры одинаковы), можно с помощью формулы: 6! = 720.
Формула
Факториал числа вычисляется по следующей формуле:
n! = n x (n-1) x (n-2) x … x 2 x 1
Где n – число, факториал которого нужно вычислить.
Например, факториал числа 5:
- 5! = 5 x 4 x 3 x 2 x 1
- 5! = 120
Таким образом, факториал числа 5 равен 120.
Вопрос-ответ:
Что такое факториал и для чего он используется в математике?
Факториал – это произведение всех натуральных чисел от 1 до этого числа включительно. Обозначается через восклицательный знак. Например, факториал 5 равен 1*2*3*4*5 = 120. Факториал используется в комбинаторике и вероятностных расчетах.
Как вычислить факториал числа?
Для вычисления факториала числа нужно умножить все натуральные числа от 1 до указанного числа. Например, чтобы вычислить факториал числа 6, нужно найти произведение: 1*2*3*4*5*6 = 720. Для больших чисел удобнее использовать специальные программы или таблицы значений факториалов.
Какова основная причина использования факториала в математике?
Факториал часто используется в комбинаторике для подсчета количества возможных вариантов разных комбинаций из заданного набора элементов. Например, комбинации из 3 элементов в наборе из 5 элементов можно вычислить как (5! / (3!*(5-3)!)) = 10. Также факториал используется вмерах вероятности для подсчета количества уникальных перестановок элементов.
Где может пригодиться знание факториала в повседневной жизни?
Знание факториала может пригодиться в повседневной жизни при решении определенных задач, таких как подсчет количества вариантов разных комбинаций (например, при выборе подарка из нескольких вариантов). Кроме того, факториал используется в математической статистике при рассчете вероятности событий и построении графиков функций.
Можно ли использовать отрицательные числа при вычислении факториала?
Нет, факториал может быть определен только для натуральных чисел. Отрицательное число или дробь не могут быть использованы при вычислении факториала. Нулевой факториал также не определен.
Каково значение 0! ?
0! имеет значение 1. Это определение было введено для удобства и соответствия математическим формулам и теориям. Эта формула используется в комбинаторике и других областях математики.
Как можно использовать факториал в программировании?
В программировании факториал может использоваться для решения различных задач, таких как генерация всех возможных перестановок элементов массива, создание и решение задач комбинаторики и т.д. Для вычисления факториала в Python можно использовать стандартную функцию “math.factorial()”.
Пример
Рассмотрим пример нахождения факториала числа 5.
-
- Переменная result принимает значение 1
Таблица значений на каждой итерацииiresult
| 1 | 1 |
-
- При первой итерации переменная i равна 1. Умножаем result на i, то есть 1 * 1 = 1. Результат сохраняем в result.
Таблица значений на каждой итерацииiresult
| 1 | 1 |
| 2 | 1 * 2 = 2 |
-
- При второй итерации переменная i равна 2. Умножаем result на i, то есть 1 * 2 = 2. Результат сохраняем в result.
Таблица значений на каждой итерацииiresult
| 1 | 1 |
| 2 | 1 * 2 = 2 |
| 3 | 2 * 3 = 6 |
-
- Аналогично продолжаем находить произведение до тех пор, пока не достигнем числа 5.
Таблица значений на каждой итерацииiresult
| 1 | 1 |
| 2 | 1 * 2 = 2 |
| 3 | 2 * 3 = 6 |
| 4 | 6 * 4 = 24 |
| 5 | 24 * 5 = 120 |
Таким образом, факториал числа 5 равен 120.
Важность в математике
Математика является одним из важнейших наук и имеет огромное значение в нашей жизни. Она даёт нам способность к анализу, логическому мышлению, решению проблем и принятию решений.
Кроме того, математика оказывает влияние на многие другие науки, такие как физика, химия, биология и др. Она позволяет создавать математические модели, которые помогают нам лучше понимать мир вокруг нас и предсказывать его развитие.
Математика важна также в экономике, финансах, компьютерных науках и других областях. Знание математики позволяет принимать правильные решения и управлять ресурсами.
С учётом всего вышеизложенного, мы можем с уверенностью утверждать, что математика играет важную роль в нашей жизни и необходима для достижения успеха в различных областях деятельности.
Как применяется в программировании
Факториал в математике имеет множество приложений в программировании. Он может использоваться для расчета комбинаторных формул, вычисления алгоритмов поиска и сортировки, а также для решения задач с деревьями.
Один из примеров применения факториала в программировании – это расчет количества перестановок. В таких случаях факториал используется для вычисления возможного количества вариантов расположения элементов.
Другой пример применения факториала – это вычисление биномиальных коэффициентов. В этом случае факториал используется для вычисления количества различных сочетаний элементов из заданного множества.
Кроме того, факториал может быть использован для определения производительности алгоритмов и программ. Например, факториал может быть использован для измерения сложности алгоритма поиска наибольшего общего делителя (НОД) двух чисел.
Также факториал широко используется в области статистики и анализа данных, где он используется для расчета вероятностей и статистических показателей.
Сложность вычисления факториала
Вычисление факториала может оказаться довольно трудоемкой задачей для больших значений. Факториал n вычисляется как произведение всех натуральных чисел от 1 до n включительно.
Чтобы вычислить факториал числа n, необходимо умножить все числа от 1 до n. При этом количество операций умножения будет равным n-1, т.е. чем больше число, тем больше операций нужно выполнить.
Например, для вычисления факториала числа 5 потребуется выполнить 4 умножения: 1*2*3*4*5=120
Однако при вычислении факториала больших чисел количество операций может стать огромным. Например, для вычисления факториала числа 1000 потребуется выполнить 999 умножений, что невозможно сделать вручную. Для решения этой задачи необходимо использовать специальные алгоритмы, которые ускоряют процесс вычисления факториала.
Существуют различные методы вычисления факториала, такие как рекурсивный, циклический, а также использование гамма-функции. Каждый из этих методов имеет свои преимущества и недостатки, поэтому выбор метода зависит от требуемой точности и скорости вычислений.
Обратный факториал
Обратный факториал – это математическая операция, обратная к нахождению факториала. То есть, если мы знаем факториал числа, мы можем найти число, которому оно равно.
Например, факториал числа 5 равен 120 (5! = 5 x 4 x 3 x 2 x 1 = 120). Чтобы найти число, которому равен 120, мы можем использовать обратный факториал. Он обозначается как !-1 и выглядит так:
5! = 120, а !-1(120) = 5
Также можно использовать табличный метод для нахождения обратного факториала. Создается таблица, в которой указываются значения факториалов и соответствующие им числа. Например:
ЧислоФакториал
| 1 | 1 |
| 2 | 2 |
| 3 | 6 |
| 4 | 24 |
| 5 | 120 |
Если нам нужно найти обратный факториал числа 24, мы можем найти его в таблице и увидеть, что соответствующее число 4.
Обратный факториал применяется в различных областях, например, в теории вероятности и численных методах.
Факториал числа 0
Факториал числа 0 является одним из наиболее простых случаев в математике. Факториал числа 0 определяется как единица.
Для того чтобы получить факториал числа 0, нужно умножить все числа между 1 и 0. Но в данном случае числа между 1 и 0 отсутствуют. Поэтому, факториал числа 0 равен 1.
Факториал числа 0 может быть использован в сочетании с другим числом при расчете факториала. Например, факториал числа 5! (5 факториал) равен 120, а это получается путем перемножения чисел 1, 2, 3, 4 и 5. Если нам нужно определить факториал числа 0 и 5 (5!), мы можем перемножить факториал числа 0, который равен 1, и факториал числа 5, который равен 120, чтобы получить ответ 1 х 120 = 120.
Интересные факты
Факториал 0 равен 1. Это звучит довольно странно, но фактически, если у нас нет ни одного объекта, то мы можем рассчитать только один способ его распределения – этот объект остается на своем месте.
Факториал может быть аппроксимирован для больших чисел. Для чтения факториала больших чисел может потребоваться много места в памяти, но люди нашли пути обхода этой проблемы. Например, числа могут быть аппроксимированы при помощи формул, что позволяет вычислять их значения без создания длинных цепочек чисел.
Факториал используется в различных областях. Кроме математики, факториал используется в физике, химии, статистике, а также в программировании, например, для определения количества возможных перестановок элементов в массиве.
- Факториал числа 10 равен 3 628 800.
- Факториал числа 20 равен 243 290 200 817 664 000.
- Факториал числа 100 равен 93 326 215 443 944 152 681 699 238 856 266 700 490 715 968 264 381 621 468 592 963 895 217 599 993 229 915 608 941 463 976 156 518 286 253 697 920 827 223 758 251 185 210 916 864 000 000 000 000 000 000 000 000 000 000 000 000.
Резюме

Факториал является одним из важнейших понятий в математике. Он определяется как произведение всех положительных целых чисел, меньших или равных данному числу. Например, факториал числа 5 равен 5 x 4 x 3 x 2 x 1 = 120.
Факториалы широко используются в математике и ее приложениях, таких как комбинаторика, теория вероятностей и статистика. Они также используются в анализе сложности алгоритмов и расчетах вероятностей в криптографии.
Вычисление факториала может быть выполнено с помощью цикла или рекурсивной функции. Для больших значений факториала могут потребоваться специальные алгоритмы, такие как алгоритм Штли, который используется для быстрого вычисления факториала больших чисел.
Знание о факториалах может быть полезным при решении различных задач в математике и ее приложениях. Также оно может помочь в повседневной жизни при решении задач, связанных с комбинаторикой и вероятностями.






