Узнайте, что такое измерение угла и как его измерить в 5 классе математики. В статье приведены примеры и подробные объяснения. Будь готов к следующему уроку по теме геометрии!
Изучение геометрии является одним из основных компонентов математического образования. Углы также включаются в программу по математике, начиная с 5 класса. Угол – это два луча, которые имеют общую точку начала. Точка начала называется вершиной угла, а лучи – сторонами. Классификация углов и их измерение являются фундаментальными принципами геометрии.
Школьники учатся измерять углы по градусам. Градус – это единица измерения угла, которая равна 1/360 полного оборота. Полный оборот составляет 360 градусов. Для измерения угла необходимо поместить его в центр круглого измерительного инструмента, называемого градусником. Затем читается значение угла в градусах на шкале градусника.
Углы используются во многих областях, включая геометрию, физику, науку о материалах, архитектуру и технику. Понимание концепций углов и их измерения является необходимым для решения многих задач в реальном мире.
Что значит измерение угла в математике для учеников 5 класса
Измерение углов – одна из основ математики, которую изучают ученики начальной школы. Угол – это геометрическая фигура, которая образуется двумя лучами, исходящими из одной точки. Один из лучей называется начальным, а другой – конечным.
Для измерения углов используют угловой прибор – это инструмент, который позволяет измерить величину угла в градусах, минутах и секундах. В школьном курсе математики ученики изучают углы, их названия, классификацию и способы измерения.
Измерение углов – это важнейший элемент при решении геометрических задач. Например, при рисовании прямых, окружностей или многоугольников, зная углы, можно точно определить форму образований.
Также основные знания о геометрических фигурах необходимы в процессе изучения многих наук, включая физику, химию и технику. Изучение углов – это первый шаг к освоению геометрической алгебры и более сложным темам в будущем.
- Ключевые моменты:
- Угол – это фигура, образованная двумя лучами.
- Угловой прибор – это инструмент для измерения углов в градусах, минутах и секундах.
- Знание углов является важным компонентом при решении геометрических задач и изучении наук в будущем.
Углы. Понятие и определение
Углы – это фигуры, которые образуются в результате пересечения двух лучей, которые имеют общее начало. Начало лучей называется вершиной угла, а концы лучей – его сторонами.
Углы измеряются в градусах (°), минутах (‘) и секундах (“), где один градус равен 60 минутам и одна минута равна 60 секундам.
Острый угол – это угол, который меньше 90°. Прямой угол – это угол, который равен 90°. Тупой угол – это угол, который больше 90°, но меньше 180°.
Углы могут быть название по размеру: малый (меньше 90°), средний (равен 90°), большой (больше 90°, но меньше 180°), нулевой (равен 0°) и полный (равен 180°).
Углы могут быть также классифицированы по форме: остроугольный (все углы меньше 90°), тупоугольный (один угол больше 90°) и прямоугольный (один угол равен 90°).
Измерение углов играет важную роль во многих областях, таких как геометрия, физика, астрономия, навигация и программирование. В школьной программе углы изучаются начиная с 5 класса.
Виды углов

Угол – это часть плоскости, ограниченная двумя лучами, имеющими один общий конец. Углы могут иметь различные формы и размеры. Различают следующие виды углов:
- Прямой угол – имеет величину 90 градусов;
- Острый угол – имеет величину меньше 90 градусов;
- Тупой угол – имеет величину больше 90 градусов, но меньше 180 градусов;
- Развернутый угол – имеет величину 180 градусов, что соответствует полной окружности.
Также углы могут быть смежными – имеющими общую сторону, вершину и лучи расположенные по разные стороны общей стороны.
Если лучи угла расположены на одной прямой, то такой угол называется прямой. Два прямых угла служат базовой единицей измерения угла – градусом.
Тип углаПример
| Прямой угол |  |
| Острый угол |  |
| Тупой угол |  |
| Развернутый угол |  |
Измерение углов в градусах
Угол — это геометрическая фигура, ограниченная двумя лучами, начало одного из которых называется вершиной угла. Измерение угла в градусах важно для решения многих задач в геометрии и физике.
Градус — это единица измерения угла. Полный угол равен 360 градусам. Одна из самых простых и первых задач в геометрии – как измерить угол – вычисляется с помощью линейки и секундомера.
Для измерения угла нужно найти вершину и пометить ее точкой. Далее, нужно на линейке отмерить одинаковые отрезки на каждом из лучей угла и соединить эти точки отметками. Затем нужно измерить время, за которое перемещается часовая стрелка на циферблате секундомера от одной отметки до другой. Для этого отметку на часовом циферблате можно начинать со стороны, откуда начинается луч угла.
После того, как время измерено, нужно воспользоваться формулой: угол в градусах равен времени в секундах, прошедшему между отметками, умноженному на 6. Например, если время, за которое переместилась часовая стрелка, равно 20 секундам, то угол будет равен 20 * 6 = 120 градусов.
Таким образом, измерение угла в градусах – это достаточно простая задача, которую можно решить с помощью линейки и секундомера. Зная угол, можно решать задачи в геометрии и физике.
Примеры задач на измерение углов
Пример 1: Найдите угол, образованный двумя отрезками, если один из них составляет 50°, а другой – 80°.
Для решения этой задачи необходимо использовать свойство суммы углов треугольника. Угол, образованный двумя отрезками, будет равен разности между углами треугольника, противолежащими этим отрезкам. Значит, мы можем найти третий угол треугольника, а затем вычесть из него известные два угла:
Угол треугольника = 180°
Угол 1 = 50°
Угол 2 = 80°
Угол 3 = 180° – 50° – 80° = 50°
Ответ: угол, образованный двумя отрезками, равен 50°.
Пример 2: Найдите угол, образованный двумя пересекающимися отрезками, если известно, что другой угол, образованный этими отрезками, равен 70°.
Для решения этой задачи необходимо использовать свойство суммы углов при пересечении двух прямых. Таким образом, мы можем найти угол, образованный двумя пересекающимися отрезками, как разность между 180° и известным углом:
Угол при пересечении прямых = 180°
Известный угол = 70°
Угол с неизвестной мерой = 180° – 70° = 110°
Ответ: угол, образованный двумя пересекающимися отрезками, равен 110°.
Пример 3: Найдите угол между биссектрисами двух углов, если известна мера одного из них равна 60°.
Для решения этой задачи необходимо использовать свойство биссектрисы угла. Мы знаем, что биссектриса угла делит этот угол на две равные части. Затем, чтобы найти угол между биссектрисами, мы используем свойство суммы углов в треугольнике. Таким образом:
Угол 1 = 60°
Угол 2 = 1/2 × 60° = 30°
Угол между биссектрисами = 180° – 60° – 30° = 90°
Ответ: угол между биссектрисами двух углов равен 90°.
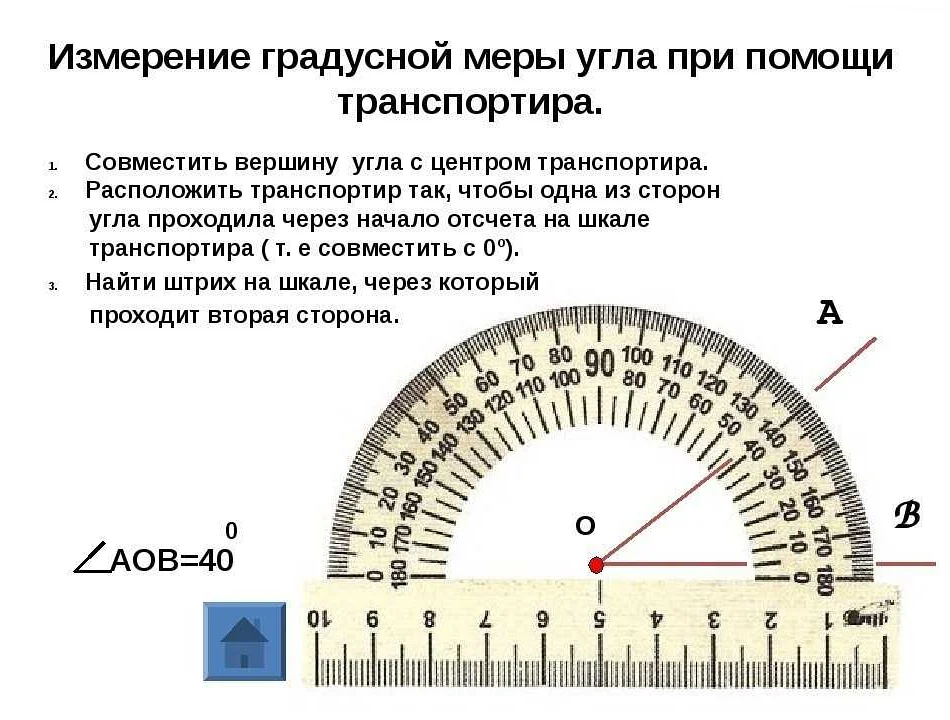
Измерение углов при помощи транспортира
Для измерения углов в математике часто используется специальный инструмент – транспортир. Он представляет собой прозрачную полупрозрачную полуокружность с делениями на градусы, от 0 до 180.
Чтобы измерить угол при помощи транспортира, нужно:
- Приложить транспортир к углу так, чтобы одна из его линий проходила через вершину угла.
- Повернуть транспортир так, чтобы другая его линия совпала с одной из линий угла.
- Прочитать значение угла по шкале транспортира на месте, где проходит его другая линия.
Обратите внимание, что на рисунке угол равен 70 градусам.
Пример измерения угла
 |
Изучение измерения углов при помощи транспортира полезно не только для математики, но и для решения практических задач. Например, измерение угла может быть полезным при постройке крыши дома или установке солнечных панелей.
Углы в ежедневной жизни
В повседневной жизни мы постоянно сталкиваемся с углами, даже не задумываясь об этом. Например, когда мы садимся за стол, мы видим угол между нашими руками и столом. Или когда мы складываем книги на полке, мы создаем угол между ними.
Углы могут быть острыми, прямыми или тупыми. Острый угол имеет меньше 90 градусов, прямой угол имеет 90 градусов, а тупой угол имеет больше 90 градусов.
Одним из применений углов в повседневной жизни являются занятия спортом. Например, гольфисты должны правильно рассчитывать угол, чтобы мячик летел в нужном направлении. Футболисты также используют углы, чтобы настроить направление своих ударов.
В строительстве также часто используются углы. Строитель должен быть в состоянии измерить угол, чтобы гарантировать, что здание или конструкция будет стоять ровно и прочно.
Измерение угла может показаться сложным, особенно для учеников 5 класса, но с помощью правильных инструментов и методов, они могут быстро освоить этот навык. Измерение углов – важный навык, который часто используется в повседневной жизни и в различных профессиях.
Как измерять углы на электронных устройствах?
Современные электронные устройства позволяют измерять углы с высокой точностью. Для этого используются специальные приложения и датчики, которые обрабатывают данные и выводят результат на экран.
Одним из наиболее распространенных способов измерения углов на электронных устройствах является использование гироскопа. Гироскоп закладывает основу для определения угла отклонения плоскости движения от вертикальной оси. Для получения точного результата, необходимо следовать инструкциям приложения и держать устройство в определенном положении.
Также можно использовать специальные приложения для измерения угла с помощью камеры смартфона или планшета. Они позволяют определить угол между объектами или поверхностями с помощью обработки изображения.
Важно помнить, что точность измерения угла на электронных устройствах зависит от самого устройства, качества датчиков и алгоритмов обработки данных. Для получения наиболее точных результатов рекомендуется использовать калибровку устройства и следить за обновлением программного обеспечения.
Видео по теме:
Вопрос-ответ:
Как измерить угол без геодезической инструментарии?
Для измерения угла можно использовать обычный транспортир или угольник. Для этого необходимо приложить его к стороне угла и считать градусы, отмеченные на инструменте.
Как правильно измерить угол между двумя отрезками в пространстве?
Для измерения угла между двумя отрезками в пространстве необходимо использовать трехмерный угольник. Он будет указывать размер угла в градусах, отмеченный на нижней части инструмента.
Как найти угол при пересечении двух прямых?
Угол между двумя пересекающимися прямыми находится как разница между двумя углами, образованными пересекающимися прямыми с третьей прямой (перпендикулярной к линиям пересечения). Два угла можно найти как сумму смежных углов.
Как измерить угол между ребрами призмы?
Для измерения угла между ребрами призмы необходимо использовать угольник, который будет показывать размер угла между двумя ребрами в градусах.
Как вычислить меру угла в градусах?
Для вычисления угла в градусах необходимо разделить его на 360 и умножить на эту же величину. Например, угол в 90 градусов равен 90/360 = 0,25, а 0,25 x 360 = 90.
Как использовать тригонометрические функции для измерения углов?
Тригонометрические функции (синус, косинус, тангенс) могут использоваться для измерения углов. Для этого необходимо использовать специальные формулы, которые связывают тригонометрические функции с мерой угла.
Как измерить угол между двумя векторами?
Угол между двумя векторами может быть вычислен с помощью скалярного произведения векторов и формулы cos(α) = a * b / (|a| * |b|), где α – мера угла, a и b – векторы, |a| и |b| – модули соответствующих векторов.
Задачи на измерение углов с использованием электронных устройств
В современном мире очень важно уметь использовать электронные устройства для решения повседневных задач. Одним из таких устройств является электронный угломер.
С его помощью можно измерять углы с высокой точностью. Этот прибор очень удобен при работе с деталями, которые необходимо собирать под определенным углом, а также при решении задач на геометрию. Последнее особенно актуально для учащихся 5 класса.
Давайте рассмотрим несколько примеров задач, которые можно решить с помощью электронного угломера:
- Найти углы треугольника. Для решения этой задачи необходимо измерить каждый угол и сложить полученные значения. Сумма углов треугольника всегда равна 180 градусов. Если полученная сумма отличается от этого значения, значит, где-то была допущена ошибка.
- Найти угол между двумя прямыми. Для этой задачи необходимо измерить углы, которые образуют данные прямые с осью координат. Затем вычесть из 180 градусов сумму полученных углов.
- Определить, является ли угол острым, прямым или тупым. Для этой задачи необходимо измерить угол. Острый угол – меньше 90 градусов, прямой угол – равен 90 градусов, тупой угол – больше 90 градусов.
Решая подобные задачи с помощью электронного угломера, учащиеся смогут не только закрепить свои знания о геометрии, но и научиться использовать современные электронные устройства в повседневной жизни.
Преимущества использования электронных устройств
Современный мир не обходится без использования электронных устройств. Они пришли на замену бумажным носителям информации и упростили нашу жизнь во многих областях.
Быстрота и эффективность
Электронные устройства позволяют обрабатывать большие объемы информации в короткие сроки. Без них было бы невозможно оперативно получать и передавать данные, осуществлять связь на большие расстояния, выполнять математические расчеты и решать другие задачи.
Мобильность и доступность
С помощью электронных устройств можно работать, учиться и развлекаться независимо от места нахождения и времени суток. Сегодня доступ к интернету, электронной почте и социальным сетям имеют не только настольные компьютеры, но и смартфоны, планшеты, ноутбуки и другие устройства. Это позволяет быть в курсе событий, коммуницировать и узнавать новое в любой момент и в любом месте.
Сохранность информации
Электронные устройства позволяют хранить и защищать информацию от доступа посторонних. При этом, электронные носители имеют большой объем памяти и могут быть очень надежными. Это удобно для хранения архивов, электронных книг, фотографий и многого другого.
Экономичность и экологичность
Использование электронных устройств снижает расходы на бумажную продукцию, что способствует экономии ресурсов и защите окружающей среды. Также, многие устройства могут заряжаться от солнечных батарей или других альтернативных источников энергии, что делает их экологически чистыми.
Универсальность и комфорт
Современные электронные устройства могут заменить целый набор инструментов и приборов, облегчая работу и повышая комфорт. Так, одновременно можно использовать смартфон для связи, навигации, замера времени и многих других функций. Это позволяет сэкономить время, деньги и ресурсы, а также облегчить жизнь и повысить её качество.






