Статья посвящена изучению корней в математике с нуля. В ней вы найдете понятные объяснения и примеры решения задач, а также полезные советы по улучшению своих навыков в этой области. Не стоит бояться сложных математических операций, у нас вы сможете легко разобраться с этой темой и достичь успеха в учебе!
Решение квадратных уравнений и вычисление корней является одним из основных элементов математики, применяемым в различных областях науки и техники. В школе ученики учатся решать уравнения с натуральными, целыми и рациональными коэффициентами, но что делать, если необходимо решить уравнение с комплексными или действительными коэффициентами и в высшей математике? Об этом и пойдет речь в данной статье.
Одним из первых шагов на пути к решению уравнений является выделение корней. Корни – это значения неизвестной величины, которые удовлетворяют уравнению. Решение уравнения состоит в вычислении этих корней. Первую возможность задачи решить уравнение в математике возникла около 4000 лет назад в Древней Месопотамии. К тому времени уравнения решали методом исчисления, а описания решения нашли на каменных табличках.
Существует несколько методов вычисления корней уравнений, но все они базируются на базовых математических принципах. В этой статье мы рассмотрим наиболее распространенные методы вычисления корней в математике и приведем примеры их применения. Также мы рассмотрим формулу дискриминанта квадратного уравнения и ее применение в определении вида корней.
Зачем нужно знать корни?
Корни – это одно из основных понятий в математике, которое используется при решении уравнений. Знание корней позволяет находить неизвестные значения и предсказывать поведение математических функций.
Например, зная корни квадратного уравнения, мы можем найти значения переменных x, чтобы уравнение выполнялось. Корни также помогают нам находить точки пересечения графиков функций и решать задачи на определение максимумов и минимумов функций.
Кроме того, знание корней является важной частью алгебры и геометрии. Оно необходимо для решения задач на нахождение периметра и площади фигур, нахождение длины дуги функции, нахождение расстояний между точками и многое другое.
Таким образом, знание корней – это необходимое условие для понимания и решения задач в математике и других науках, где используются математические методы и модели.
Определение понятия “корень”
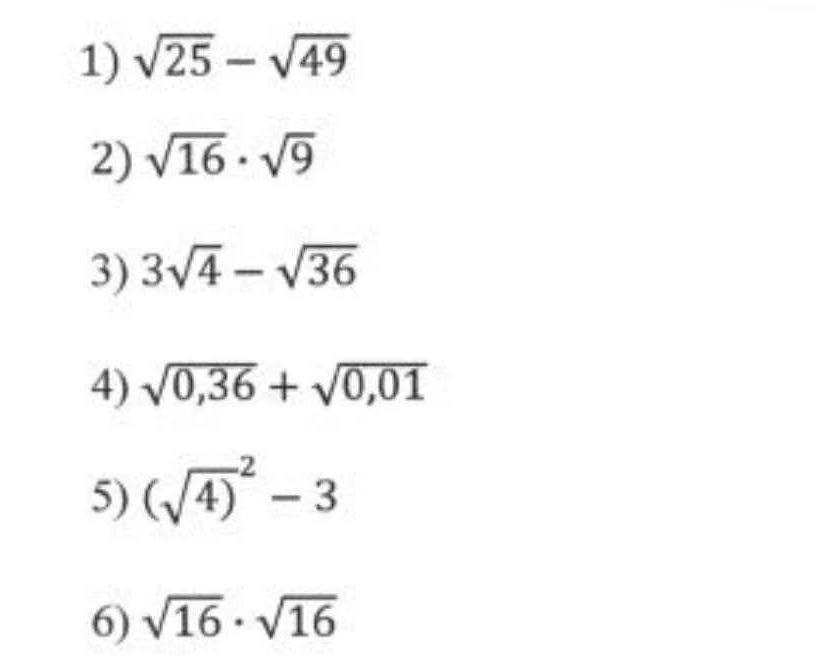
В математике корнем называют число, которое при возведении в некоторую степень даёт другое заданное число. Например, корнем числа 16 является число 4, так как 4²=16.
Корень положительного числа n обозначается символом √n и называется рациональным, если он представим в виде дроби m/n, где m и n — целые числа, а n ≠ 0. Целочисленным называется корень, который можно получить из целого числа.
Корни используются в различных областях математики и естественных науках, таких как физика, химия, технические науки и другие. Они позволяют решать уравнения, находить значения функций, а также проводить анализ и моделирование различных процессов.
В зависимости от типа числа и степени, корни могут быть рациональными, иррациональными, комплексными и т.д. Процесс извлечения корня из числа называется радикацией. Радикалы являются одним из важных понятий в алгебре и математическом анализе.
Как найти корень числа в ручную?
Найти корень числа в ручную может показаться сложным и трудоемким процессом, однако с некоторыми базовыми знаниями математики его можно освоить без проблем. Вот несколько шагов, которые помогут вам найти корень числа.
- Выберите число, корень которого вы хотели бы найти.
- Разложите число на множители. Чаще всего для нахождения корня используют разложение числа на простые множители.
- Выделите некоторые из этих множителей, которые составляют квадраты чисел.
- Разделите число на произведение этих квадратов. Это даст вам ответ.
Например, если вы хотите найти корень из числа 144, то можете разложить его на множители 2 и 72, которые затем разложите на 2, 36 и т.д. Выделите квадраты, которые составляют 2² × 6² и разделите 144 на их произведение 4 × 36. Деление даст вам ответ 6, что и является корнем из 144.
Несколько раз выполните подобные примеры и вы сможете находить корни из чисел без проблем.
Метод Ньютона. Примеры решения корней
Метод Ньютона – это численный метод нахождения корней дифференцируемой функции. Он основан на идее последовательного приближения корня с помощью касательной к графику функции.
Для выполнения метода Ньютона нужно задать начальное приближение x0 и выразить следующее приближение x1 через предыдущее x0:
x1 = x0 – f(x0) / f'(x0)
где f(x) – дифференцируемая функция, f'(x) – ее производная.
Приведем пример решения уравнения x2 – 4 = 0 с помощью метода Ньютона:
- Выбираем начальное приближение x0 = 2.
- Вычисляем значение функции f(x) = x2 – 4 и ее производной f'(x) = 2x в точке x0 = 2: f(2) = 0, f'(2) = 4.
- Находим следующее приближение x1: x1 = 2 – 0 / 4 = 2.
- Проверяем, достигнут ли корень с заданной точностью. Если нет, повторяем шаги 2-3.
Получаем, что корень уравнения x2 – 4 = 0 равен 2.
Метод Ньютона применяется для решения уравнений и систем уравнений. Его преимущество в том, что он сходится быстрее, чем многие другие численные методы, но также более чувствителен к начальному приближению.
Как вычислить квадратный корень?
Квадратный корень – это обратная операция возведения числа в квадрат. Например, корень из 25 это 5, так как 5 в квадрате равно 25. Квадратный корень можно вычислить с помощью специального знака √ или функции sqrt() в программировании.
Для того, чтобы вычислить квадратный корень вручную, нужно найти число, которое возведенное в квадрат будет наиболее близким к исходному числу, а затем провести несколько простых алгоритмических действий.
Например, для того, чтобы вычислить корень из 36, можно начать с предположения, что корень примерно равен 6. Затем нужно возвести это предположение в квадрат, чтобы проверить его точность: 6 * 6 = 36.
Если предположение верно, то результат найден. Если нет, то нужно продолжать процесс, приближаясь к корню. Например, можно предположить, что корень равен 7. Тогда нужно возвести 7 в квадрат: 7 * 7 = 49. Это число уже больше, чем 36. То есть корень должен быть меньше 7. Пробуем предположить, что он равен 6.5…
Таким образом, нужно продолжать процесс, уточняя предполагаемое значение корня и проверяя его точность методом проб и ошибок.
Второй знак после запятой при нахождении квадратного корня

Когда мы решаем задачи в математике, часто приходится находить квадратный корень из дробного числа. При этом может возникнуть вопрос, как найти вторую цифру после запятой в ответе.
Для этого достаточно использовать округление до второго знака после запятой. Так, если результатом вычислений будет число 3,125, то округлив его до второго знака после запятой, получим 3,13.
Также можно использовать метод, который называется методом Ньютона. Он заключается в повторении вычисления несколько раз с уточнением результата. Этот метод используется в тех случаях, когда требуется большая точность.
Итак, при нахождении квадратного корня из числа, чтобы найти вторую цифру после запятой, нужно использовать округление до второго знака или метод Ньютона.
Что такое иррациональные числа?
Иррациональные числа – это числа, которые нельзя представить в виде дроби, где числитель и знаменатель являются целыми числами. Такие числа имеют бесконечное количество десятичных цифр после запятой, но не имеют периодической структуры.
Примеры иррациональных чисел: √2, π, e. Они невозможно точно представить в виде дроби, но могут быть приближены сколь угодно близко.
Иррациональные числа приводят к интересным математическим проблемам и способны удивлять своими свойствами. Они встречаются в геометрии, теории чисел, анализе и многих других областях математики.
Некоторые иррациональные числа появляются в природе, например, π используется для расчетов окружности, а число φ (золотое сечение) связано с геометрией искусства и фракталами.
Интересно, что сочетание иррациональных и рациональных чисел может создать новые иррациональные числа. Например, сумма √2 и 2 является иррациональным числом, а сумма двух рациональных чисел обычно является рациональным числом.
Иррациональные числа имеют важное значение в математике, науке и технологии, и изучение их свойств может привести к новым открытиям и применениям.
Приближенное вычисление корней
Приближенное вычисление корней – это метод, который используется для нахождения корня уравнения, когда нет возможности найти его аналитически, т.е. точно.
Один из наиболее популярных методов приближенного вычисления корней – метод равномерного деления отрезка пополам (метод бисекции). Для его применения необходимо определить отрезок, на котором существует корень уравнения. Затем отрезок делится пополам и определяется, на какой из частей находится корень. Этот процесс повторяется до тех пор, пока не достигнется требуемая точность или не будет найден корень.
Другой метод приближенного вычисления корней – метод Ньютона. Он основан на использовании производной функции для нахождения более точного приближения к корню. При этом начальное приближение выбирается произвольно, а затем вводится формула, которая позволяет уточнить приближение. Этот процесс также повторяется до достижения требуемой точности.
Независимо от метода приближенного вычисления корней, важно помнить о необходимости выбирать начальное приближение точно и проводить достаточное количество итераций, чтобы достигнуть нужной точности.
- Метод равномерного деления отрезка пополам является простым в использовании и требует меньше вычислительных ресурсов, чем метод Ньютона.
- Метод Ньютона обычно сходится быстрее, но может быть более чувствителен к выбору начального приближения и может зациклиться, если производная функции близка к нулю.
В заключение, приближенное вычисление корней является важным инструментом в математике, который позволяет находить корни уравнений, когда аналитическое вычисление невозможно. Методы равномерного деления отрезка пополам и Ньютона являются наиболее известными методами, которые могут быть использованы для этой цели.
Решение квадратных уравнений на пальцах

Квадратное уравнение – это уравнение вида ax2 + bx + c = 0, где a, b и c – некоторые числа, а переменная x принимает значения.
Для решения квадратного уравнения на пальцах, нужно знать формулу, которая выглядит так: x = (-b ± √(b2-4ac)) / 2a
Здесь нужно раскрыть скобки и вычислить корни. Чтобы упростить себе задачу, можно записать таблицу со всеми значениями и постепенно проводить вычисления.
abcДискриминантКорни
| 1 | 2 | 1 | 0 | x = -1 |
| 1 | 5 | 6 | 1 | x1 = -2, x2 = -3 |
| 1 | -3 | 2 | 1 | x1 = 2, x2 = 1 |
Если дискриминант (b2-4ac) равен нулю, то уравнение имеет только один корень x = -b/2a. Если дискриминант больше нуля, то уравнение имеет два корня. Если же дискриминант отрицательный, то действительных корней уравнение не имеет.
Важно помнить, что этот метод решения квадратных уравнений на пальцах является одним из самых простых, но не всегда применим. Некоторые уравнения могут быть решены только численными методами и методами анализа функций.
Задачи на корни в школьной программе

Корень числа – это число, возведенное в эту степень даёт данное число. В школьной программе можно столкнуться с задачами на корни разных порядков. Рассмотрим некоторые из них.
- Задачи на нахождение корней квадратных уравнений. Квадратное уравнение имеет вид ax²+bx+c=0. Его решениями являются два корня: x₁=(-b+√D)/2a и x₂=(-b-√D)/2a, где D=b²-4ac. В школе учат находить два корня квадратного уравнения с помощью формулы и сведения уравнения к квадрату.
- Задачи на вычисление корня из числа. В школе дети учатся вычислять корень из числа с помощью извлечения корня по ступеням (т.е. нахождения корня из каждой цифры числа по отдельности) и с помощью метода Ньютона (итерационный метод нахождения корня).
- Задачи на нахождение площади фигур с корнями. Например, для нахождения площади треугольника со сторонами a, b, c можно воспользоваться формулой Герона: S=√p(p-a)(p-b)(p-c), где p=(a+b+c)/2 – полупериметр треугольника.
Задачи на корни являются важной частью школьной программы и помогают развивать логическое мышление и умение работать с формулами и уравнениями.
Использование корней в жизни
Корни – это понятие, которое приходится использовать в разных сферах жизни. Например, в строительстве корни используются для расчета длины кабеля, необходимого для проведения электрического тока на большие расстояния.
В области финансов математические корни используются для расчета сложных процентов и анализа рисков вложений. Это помогает инвесторам принимать взвешенные решения и минимизировать риски.
В биологии корни – это неразрывно связанный с землей элемент растительного мира. Через корни растения получают воду и питательные вещества, они же служат опорой для стеблей и листьев.
Кроме того, математические корни используются в геометрии для расчета длин сторон и диагоналей фигур.
Таким образом, корни – это неотъемлемая часть нашей жизни, которая помогает нам в решении разных задач и проблем.
Вопрос-ответ:
Как начать изучать корни в математике?
Начните с изучения определения корня, основных свойств и примеров решения задач. Затем решайте уровневые задачи, постепенно усложняя их.
Как вычислить корень из натурального числа?
Для вычисления корня из натурального числа используется радикал. Например, корень квадратный из 25 равен 5, так как 5 * 5 = 25.
Как решать задачи на нахождение корней?
Для решения задач на нахождение корней необходимо уметь переходить от равенства к корню и обратно, использовать свойства корня и алгебраические преобразования.
Как вычислить корень из отрицательного числа?
Корень из отрицательного числа нельзя вычислить в рамках действительных чисел. Для этого используют комплексные числа.
Какие ошибки чаще всего допускают при работе с корнями?
Ошибки могут быть связаны с неправильным применением свойств корня, неправильным переходом от равенства к корню и обратно, неправильным вычислением корня из отрицательного числа.
Как связаны корни многочлена и его коэффициенты?
Коэффициенты многочлена определяют его корни. Например, многочлен x^2 – 5x + 6 имеет корни 2 и 3, так как (x-2)*(x-3) = x^2-5x+6.
Как использовать корни в решении задач физики?
Корни используются в задачах, связанных с вычислением силы тяжести, равновесия, колебаний и др. Например, в задаче о свободном падении тела на Земле используется корень из ускорения свободного падения, равный 9,81 м/c^2.






