Узнайте, как правильно составить математическую модель с помощью нашей статьи. Мы расскажем о шагах, которые нужно сделать, чтобы построить точную и эффективную модель. Получите полезные советы и рекомендации от наших экспертов прямо сейчас.
Математическое моделирование – это процесс представления реального объекта или явления в виде математических формул. Это позволяет описать объект с использованием вычислительных средств и проанализировать его поведение в различных условиях. Моделирование широко используется в различных сферах, например, в экономике, физике, медицине и технике.
Чтобы правильно составить математическую модель, необходимо иметь хорошее представление о сущности исследуемого объекта и его особенностях. Необходимо также выбрать подходящую математическую модель, которая позволит наилучшим образом описать объект и его взаимодействие с окружающей средой.
При составлении математической модели следует использовать различные математические методы и инструменты, например, дифференциальные уравнения, интегральные уравнения, теорию вероятностей и другие. Важно учитывать также факторы, которые могут влиять на поведение объекта, например, изменения внешней среды, воздействие других объектов или изменения в условиях эксплуатации.
В итоге, математическая модель позволяет получить более глубокое понимание поведения исследуемого объекта и предсказать его дальнейшее развитие. Кроме того, математическое моделирование позволяет оптимизировать процессы, уменьшить затраты и сократить время на разработку и испытания новых продуктов и технологий.
Как создать математическую модель
Математическая модель – это абстрактная структура, созданная для описания и изучения реального явления. С помощью математической модели мы можем оценивать возможные последствия изменений параметров системы и принимать решения на основе этих прогнозов. Важно понимать, что для создания математической модели необходимо понимание принципов работы системы, которую мы хотим моделировать.
Для создания математической модели необходимо собрать данные о системе и разработать уравнения, описывающие ее поведение. Уравнения должны отображать зависимости между различными элементами системы и качественно описывать эти зависимости. Для этого необходимо использовать знания математики, в том числе теорию вероятности, дифференциальные уравнения, статистику и др.
Важно также проверять математическую модель на соответствие реальной системе. Для этого проводятся эксперименты, которые позволяют оценить точность и применимость модели. Если модель не соответствует реальности, то необходимо внести изменения и усовершенствовать ее.
- Шаг 1: Понимание принципов работы системы
- Шаг 2: Сбор данных о системе
- Шаг 3: Разработка уравнений, описывающих поведение системы
- Шаг 4: Проверка модели на соответствие реальности
- Шаг 5: Изменение и усовершенствование модели (если необходимо)
Важно помнить, что математическая модель – это лишь упрощенное описание реальности, которое необходимо для принятия решений. Однако, хорошо спроектированная и проверенная модель может помочь в достижении целей более эффективно и точно, что делает ее важным инструментом в различных областях науки, техники, экономики и т. д.
Определение проблемы
Определение проблемы – это первый этап в составлении математической модели. На этом этапе необходимо определить, что именно требуется решить или объяснить с помощью модели.
Пример: Компания хочет определить оптимальное количество рабочих дней в неделю для достижения максимальной производительности, с учетом затрат на оплату труда.
Шаги определения проблемы:
- Определение цели: что именно нужно решить или объяснить с помощью модели.
- Описание ситуации: каким образом работает система, ситуация или процесс, который требуется исследовать.
- Идентификация основных переменных: какие величины и параметры могут влиять на ситуацию и каких данных необходимо для их анализа.
Пример: Цель – определить оптимальное количество рабочих дней в неделю. Ситуация – производство, работающее в определенные часы, с определенным штатом сотрудников. Основные переменные – количество рабочих дней в неделю, производительность, затраты на оплату труда.
В результате определения проблемы получается более ясное представление о том, что необходимо решить и какие данные могут быть использованы при создании математической модели.
Сбор данных
Первый шаг в составлении математической модели – это сбор данных. Сбор данных представляет собой тщательный процесс сбора информации, необходимой для создания модели. Данные могут быть получены из различных источников, включая статистические данные, наблюдения, опросы или иные источники информации.
Сбор данных требует особой внимательности и точности. Ключ к сбору данных является точность их качества, поэтому данные должны быть собраны так, чтобы их можно было использовать в качестве основы для математической модели.
Для успешного сбора данных необходимо определить источники данных и выбрать методы сбора данных. Методы сбора данных могут варьироваться в зависимости от источника данных, включая опросы, наблюдения и прочие источники. Кроме того, для минимизации ошибок, связанных со сбором данных, необходимо убедиться, что данные собираются согласно определенным протоколам и в соответствии с заранее определенными требованиями.
Кроме того, необходимо проводить проверку качества данных на протяжении всего процесса сбора данных. Это может быть сделано через тестирование, проверку различных факторов и пр., чтобы убедиться в точности данных. Важно убедиться, что собранные данные действительно отражают выборку, которую мы исследуем.
Итак, сбор данных – это главный шаг в создании математической модели. Чтобы сделать это эффективно, нужно определить источники данных, выбрать методы сбора данных и проводить проверку качества данных на протяжении всего процесса.
Анализ данных
Анализ данных – это процесс изучения информации и получения новых знаний о явлениях, процессах и объектах. Он помогает увидеть закономерности и связи в данных и принимать более обоснованные решения. В мире больших данных анализ данных становится все более важным и незаменимым инструментом для бизнеса и науки.
Для проведения анализа данных необходимо собрать данные и подготовить их для обработки. Затем следует выбрать методы анализа, которые позволят получить нужную информацию из данных. Эти методы могут включать в себя статистические методы, машинное обучение и другие алгоритмы математического моделирования.
- Статистический анализ может использоваться для определения статистически значимых различий между группами данных, а также для определения корреляции между переменными.
- Машинное обучение позволяет создавать алгоритмы, которые могут обнаруживать закономерности в данных и создавать модели, которые могут использоваться для прогнозирования будущих результатов.
После проведения анализа данных необходимо интерпретировать полученные результаты и принимать решения на основе полученной информации. Анализ данных может помочь выявить проблемы и возможности, которые не были замечены ранее, и сделать более обоснованные решения на основе данных.
Выбор подходящей модели

Для того чтобы построить математическую модель, необходимо выбрать подходящую формулу или алгоритм, который бы описывал процесс или явление, на которое направлена модель. Однако, выбор подходящей модели не всегда простой задачей.
Важно учитывать специфику задачи и иметь достаточное количество данных для того, чтобы проверить и адаптировать выбранную модель. Модели можно классифицировать по типу данных, которые они используют, по степени аппроксимации, по типу функций или алгоритмов, которые демонстрируют и др.
Для выбора подходящей модели можно использовать итеративный подход, когда каждая модель проверяется на заданных данных, пока не будет найдена подходящая. Также можно использовать статистические методы, которые позволят оценить точность и качество модели.
Важно помнить, что выбранная модель должна иметь достаточную точность для решения поставленной задачи, но не стоит стараться описать все нюансы процесса до мелочей, так как это может привести к необходимости использования слишком сложных моделей, которые будут трудно интерпретировать и адаптировать в будущем.
- Выбирайте модель, которая наилучшим образом описывает процесс или явление
- Учитывайте специфику задачи и имейте достаточное количество данных
- Проверяйте каждую модель на заданных данных и используйте статистические методы для выбора подходящей модели
- Выбранная модель должна иметь достаточную точность, но не стоит описывать все нюансы процесса до мелочей и использовать слишком сложные модели
Формулирование гипотезы
Для создания математической модели необходимо определить гипотезу, которая будет основой моделирования. Гипотеза – это предположение о том, как работает процесс или система.
При формулировании гипотезы нужно, чтобы она была четкой, конкретной и проверяемой. Это позволит проверить ее правильность и определить достоверность полученных результатов.
Важно учитывать, что гипотеза должна быть основана на знаниях о системе и процессе, которые уже имеются, исходя из имеющихся данных и опыта. Она также должна быть логически последовательной и объективной, не должна содержать предвзятости в отношении тех или иных результатов.
Когда гипотеза сформулирована, ее следует проверить на основе имеющихся данных. При этом важно, чтобы результаты были проанализированы и интерпретированы правильно, а сама гипотеза подтвердилась или опроверглась.
В целом, формулирование правильной гипотезы – это важный этап в создании математической модели, который определяет ее точность и достоверность. Он требует внимательного и основательного подхода, но, стоит приложить усилия, результат будет ключевым в достижении целей моделирования.
Построение математической модели
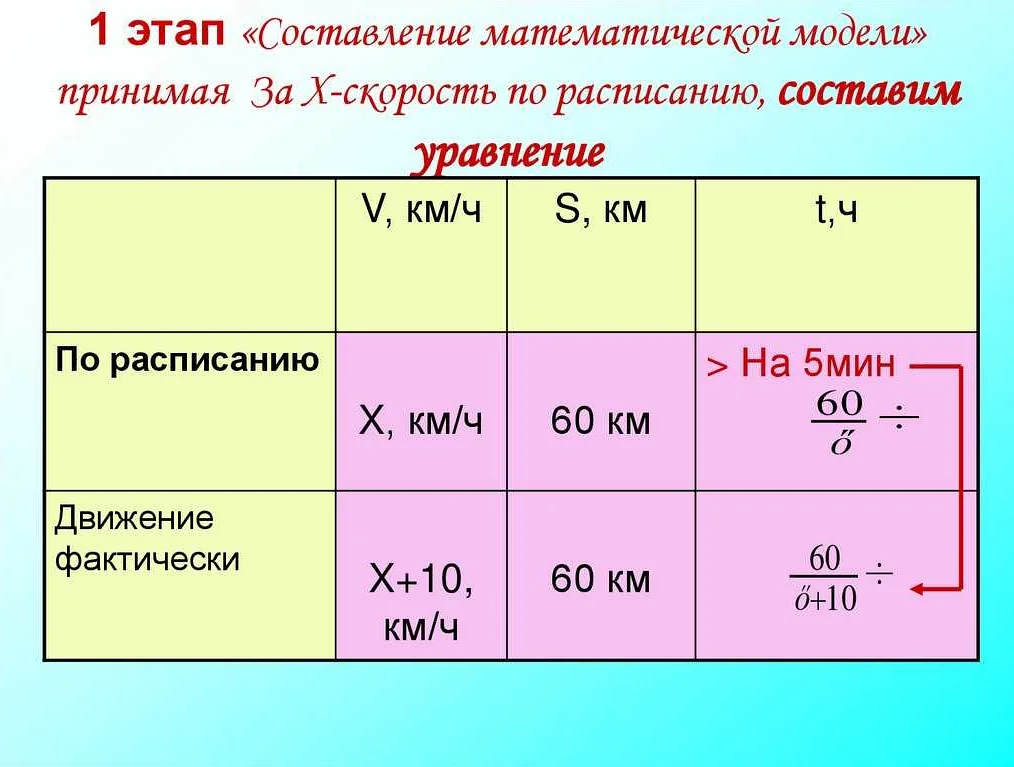
Построение математической модели является важной задачей во многих областях науки и техники. Она позволяет описать явления и процессы, предсказывать их поведение и совершать различные аналитические вычисления.
В процессе построения математической модели необходимо определить ее цель, выбрать подходящие переменные и параметры, и установить связи между ними. Важно также проводить эксперименты и наблюдения, чтобы получить данные для проверки и корректировки модели.
Существует несколько типов математических моделей, включая аналитические модели, дискретные модели, стохастические модели и дифференциальные модели. Выбор типа модели зависит от цели и особенностей рассматриваемого явления.
Математические модели широко используются в различных областях, включая физику, экономику, биологию, инженерию и т.д. Они позволяют прогнозировать и оптимизировать процессы, улучшать качество продуктов и услуг, разрабатывать новые технологии и методологии.
Построение математической модели – это сложный и многогранный процесс, требующий знаний и опыта в соответствующих областях. Но правильно построенная модель может стать мощным инструментом для принятия решений и достижения успеха в науке и бизнесе.
Тестирование модели
Тестирование математической модели – это процесс, в результате которого производится оценка эффективности модели в решении задач. Обычно тестирование включает в себя проверку модели на реальных данных или на данных, созданных специально для проверки.
Одним из способов тестирования математической модели является ввод данных в модель и анализ результатов. Если результаты соответствуют ожиданиям, то можно утверждать, что модель работоспособна. Если же результаты не соответствуют ожиданиям, то необходимо провести анализ входных данных и проверить модель на наличие ошибок.
Важно помнить, что тестирование математической модели должно быть проведено несколько раз на разных данных для проверки ее универсальности и реагирования на различные сценарии.
Также при тестировании математической модели необходимо принимать во внимание ограничения модели, возможные погрешности при вычислениях и неопределенность данных. В случае обнаружения проблем в работе модели, необходимо провести дополнительный анализ и модифицировать модель.
Тестирование математической модели – это важный этап ее создания, который помогает убедиться в работоспособности и эффективности модели в решении задач.
Калибровка модели
Калибровка математической модели – это процесс, который помогает уточнить настройки модели и сделать ее более точной. Для этого используются различные методы, например, сравнение результатов моделирования с экспериментальными данными, оптимизация параметров модели, анализ чувствительности модели к различным воздействиям и т.д.
Один из наиболее распространенных методов калибровки – метод наименьших квадратов. Он заключается в выборе таких параметров модели, которые минимизируют расстояние между значениями, полученными при моделировании, и результатами эксперимента. Данный метод помогает достичь наилучшей согласованности модели с имеющимися данными.
Также важно помнить, что калибровка модели может быть многократной. То есть после настройки модели и получения оптимальных параметров, их могут потребоваться уточнить, если появятся новые данные или изменятся условия, при которых производится моделирование. В этом случае необходимо провести новый этап калибровки для получения более точных результатов.
Таким образом, калибровка модели – это важный этап при работе с математическими моделями, который позволяет достичь наилучшей согласованности модели с имеющимися данными и увеличить точность ее прогнозов.
Валидация модели
После того, как математическая модель была построена, необходимо ее проверить на правильность и соответствие реальности. Этот процесс называется валидацией модели.
Для начала необходимо убедиться в правильности выбора переменных и параметров модели. Во многих случаях, возможны различные комбинации переменных, и необходимо выбрать те, которые наиболее точно описывают изучаемую систему.
Далее, необходимо проверить правильность использования уравнений и формул, выбранных для построения модели. Это может быть сделано с помощью анализа измерений и сравнения результатов, полученных с помощью модели и реальных экспериментов.
Также необходимо проверить модель на стабильность и повторяемость результатов. Это гарантирует, что модель может быть использована для прогнозирования будущих событий и изменений в исследуемой системе.
- Валидация модели является важной частью процесса ее построения.
- Необходимо проверить правильность выбора переменных и параметров.
- Также нужно проверить правильность использования уравнений и формул.
- Модель должна быть проверена на стабильность и повторяемость результатов.
Применение модели на практике
Составление математической модели – это важный и иногда сложный процесс, но его результаты могут быть очень полезны на практике. Модель может помочь ученым и инженерам предсказать поведение системы, оценить ее производительность и найти возможные слабые места.
Примером применения математической модели может служить моделирование таких систем, как автомобили, самолеты, системы управления транспортом, финансовые и экономические системы и многие другие. Это позволяет оценить их характеристики до физической реализации в масштабах настоящего объекта.
Модель может быть использована для определения оптимальных решений в различных сферах деятельности. Например, модель может определить оптимальные цены на товары, оптимальные маршруты доставки грузов, оптимальное время работы производственной линии или оптимальное использование ресурсов. Это помогает компаниям увеличить доходы и снизить затраты.
Также, математические модели могут быть использованы для анализа данных и прогнозирования будущих трендов и событий. Это может быть полезным в инвестиционной деятельности, прогнозировании продаж и выборе стратегии компании.
В целом, использование математической модели на практике может привести к улучшению бизнес-процессов, оптимизации использования ресурсов и повышению производительности систем и компаний в целом.
Обновление модели
Обновление математической модели является необходимым процессом для достижения максимальной точности и эффективности ее использования. Как правило, модель требует обновления при изменении параметров или условий, на которые она влияет.
Перед обновлением модели необходимо провести подробный анализ ее текущего состояния. Это включает в себя оценку точности, проверку выполнения базовых уравнений и тестирование модели на новых данных.
Одним из основных методов обновления модели является введение новых параметров и уравнений, учитывающих измененные условия. При этом необходимо стремиться к максимальной простоте модели, чтобы избежать избыточности и снизить сложность вычислений.
Также необходимо учитывать, что обновление модели может привести к неожиданным результатам, поэтому необходимо проводить тщательное тестирование и сравнение результатов с реальными наблюдениями. Важно помнить, что математическая модель является всего лишь приближением реальной ситуации и не может учитывать все факторы, влияющие на процесс.
Таким образом, обновление математической модели является важным и неотъемлемым процессом в ее разработке и использовании. Оно способствует повышению ее точности и эффективности, а также помогает улучшать прогнозирование и принимать более обоснованные решения в реальных условиях.
Вопрос-ответ:
Какие шаги нужно выполнить, чтобы составить математическую модель?
Первым шагом необходимо понять, какие переменные влияют на решаемую задачу и как они связаны между собой. Затем стоит сформулировать математические уравнения, описывающие взаимодействие этих переменных. После этого следует провести анализ и проверку модели на соответствие поставленной задачи.
Какие математические методы используются для составления моделей?
Для составления математических моделей используются различные методы, включая статистический анализ, алгебраические и дифференциальные уравнения, булевы функции, теорию вероятностей и др.
Какие навыки необходимо иметь для успешной работы с математическими моделями?
Для работы с математическими моделями необходимы знания в области математики, статистики и информатики. Также важны навыки логического мышления, умение анализировать данные и принимать взвешенные решения.
Как проводится проверка математической модели?
Проверка математической модели проводится с помощью сравнения результатов, полученных на основе модели, с фактическими данными. Также модель может быть проверена на различных задачах и оценена на предмет ее эффективности и точности.
Какие существуют проблемы при создании математических моделей?
Одной из основных проблем при создании математических моделей является нехватка данных или их некачественность. Также может возникнуть проблема выбора подходящего математического метода и настройки параметров модели.
Можно ли использовать одну и ту же математическую модель для решения разных задач?
Да, можно. Однако, для каждой конкретной задачи необходимо произвести настройку параметров модели и проверить ее на соответствие задаче.
Какие преимущества может дать использование математических моделей в решении задач?
Использование математических моделей позволяет проводить более точный анализ данных, прогнозировать различные ситуации и принимать обоснованные решения. Это может помочь снизить затраты и улучшить продуктивность бизнеса, а также обеспечить безопасность и эффективность различных процессов.






