Круглые тела в математике – это трехмерные геометрические фигуры, имеющие форму сферы, цилиндра, конуса и т.д. Научитесь распознавать их, разберитесь, какие свойства они имеют, и как их рассчитывать.
В математике, круглыми телами называются граничные объекты в трехмерном пространстве, которые образуются вращением двумерной фигуры вокруг оси.
Эти тела могут иметь различные формы – от сферы до цилиндра и конуса. Круглые тела часто встречаются в естественных науках и инженерии, поэтому их изучение имеет важное практическое значение.
В математике круглые тела широко изучаются в рамках геометрии и алгебры, для того чтобы понимать их свойства и уметь рассчитывать объем, площадь поверхности и другие характеристики.
Круглые тела в математике: все, что вам нужно знать
Круглые тела – это тела, которые могут быть описаны круговой или эллиптической поверхностью. Эти фигуры имеют большое значение в геометрии, физике и инженерных науках.
Одним из наиболее известных круглых тел является сфера. Сфера – это круглое тело, у которого каждая точка на поверхности находится на одинаковом расстоянии от центра. Объем сферы можно вычислить по формуле V = (4/3)πr³, где r – радиус сферы, π – число пи.
Другим известным круглым телом является цилиндр. Цилиндр – это тело, у которого основание и верхняя и нижняя крышки имеют форму круга, а боковая поверхность представляет собой прямоугольный параллелепипед. Объем цилиндра можно вычислить по формуле V = πr²h, где h – высота цилиндра.
Другие примеры круглых тел включают конус, тор, шарнир и т.д. Круглые тела широко используются в производстве и конструировании для создания деталей, машин и сооружений, таких как мосты и здания. Некоторые известные строения, такие как Эйфелева башня и Гуггенхайм-музей, используют круглые формы и круглые тела в своем дизайне.
Суммируя, круглые тела – это важная тема в математике и инженерии. Их формулы и свойства не только позволяют рассчитывать объемы и площади поверхности, но и дают возможность создавать красивые и эффективные конструкции. Поэтому, знание круглых тел является необходимым и полезным для всех, кто занимается наукой и технологией.
Видео по теме:
Определение круглых тел
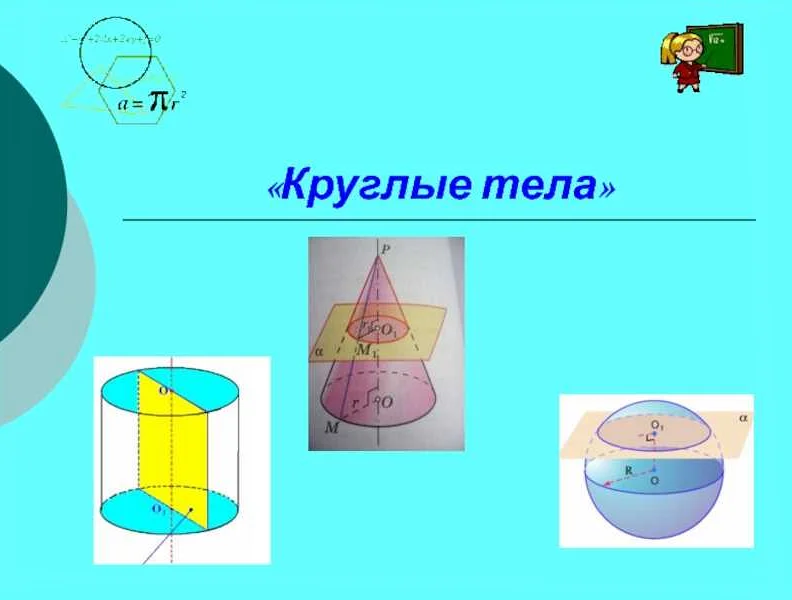
Круглыми телами в математике называют геометрические фигуры, имеющие форму сферы или цилиндра. В отличие от плоских фигур, круглые тела имеют три измерения – длину, ширину и высоту.
Сферы являются примером круглых тел, которые имеют форму шара. Они обладают радиусом, который является расстоянием от центра сферы до любой точки на ее поверхности. В математике сферы часто используются, чтобы решать задачи настолько разных областей, как физика и геодезия.
Цилиндры состоят из двух круговых плоскостей, которые называются основаниями цилиндра и боковой поверхности, которая является прямоугольной. Радиус оснований цилиндра является расстоянием между центром окружностей, которые образуют основания, и гранью цилиндра, где две окружности пересекаются.
Круглые тела не только имеют важное значение в математике, но также находят свое применение в реальной жизни. Например, многие инструменты и механизмы имеют форму цилиндра, включая бутылки, консервные банки и канистры для бензина. Сферы также используются во многих промышленных и технических приложениях, включая производство шариковых подшипников и лампочек.
Признаки круглых тел
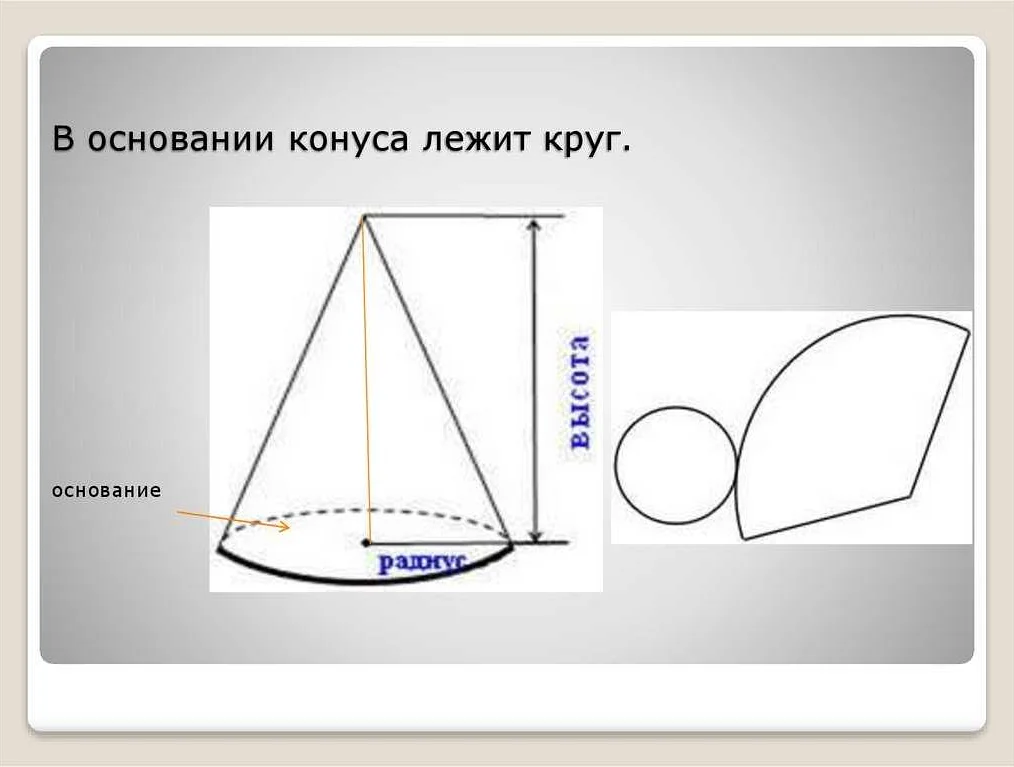
Круглость поверхности: главным признаком круглых тел является свойство поверхностей этих тел быть круглыми. Это означает, что поверхность круглого тела может быть описана с помощью круга, который расположен на этой поверхности.
Равномерность распределения: внутри круглых тел равномерно распределены все точки. Это означает, что любой диаметр, проводимый через тело, будет проходить через центр тела. Кроме того, расстояние от центра круглого тела до любой точки на его поверхности будет одинаковым.
Инвариантность формы: круглое тело имеет инвариантную форму. Это означает, что форма тела сохраняется при любом его перемещении или вращении. Например, шар сохранит свою форму независимо от того, как его повернуть или передвинуть в пространстве.
Отсутствие ребер и углов: круглые тела не имеют ребер и углов. Вместо этого у них есть гладкие кривые и изогнутые поверхности, которые их определяют. Из-за отсутствия ребер и углов нельзя разложить круглое тело на грани или части.
Разновидности круглых тел
Круглые тела – это геометрические фигуры, которые имеют форму сферы, шара или гемисферы. Круглые тела применяются в различных областях математики, физики, астрономии и техники. В зависимости от формы, круглые тела могут иметь различные свойства и характеристики.
Сфера – это круглое тело, которое имеет одинаковые расстояния от центра до всех точек на его поверхности. Сферы используются, например, для моделирования планет и звезд в астрономии, а также для создания костылей и шариков для игр.
Шар – это круглое тело, которое также имеет одинаковые расстояния от центра до всех точек на его поверхности. Шары используются в физике и механике для моделирования движения мячей и других объектов.
Гемисфера – это половина сферы, которая образуется плоскостью, проходящей через ее центр. Гемисферы используются в архитектуре и строительстве для создания куполов и других крышных конструкций.
Круглые тела также могут быть объединены для создания более сложных фигур, таких как цилиндры и конусы. Например, цилиндр состоит из двух параллельных круговых боковых поверхностей и одной прямой боковой поверхности. Конус состоит из круговой и одной конической боковой поверхности.
Более подробно изучить разновидности круглых тел можно в двумерной геометрии или в пространственной геометрии в рамках школьной программы. Это поможет лучше понять свойства круглых тел и применять их в практических задачах.
Характеристики круглых тел
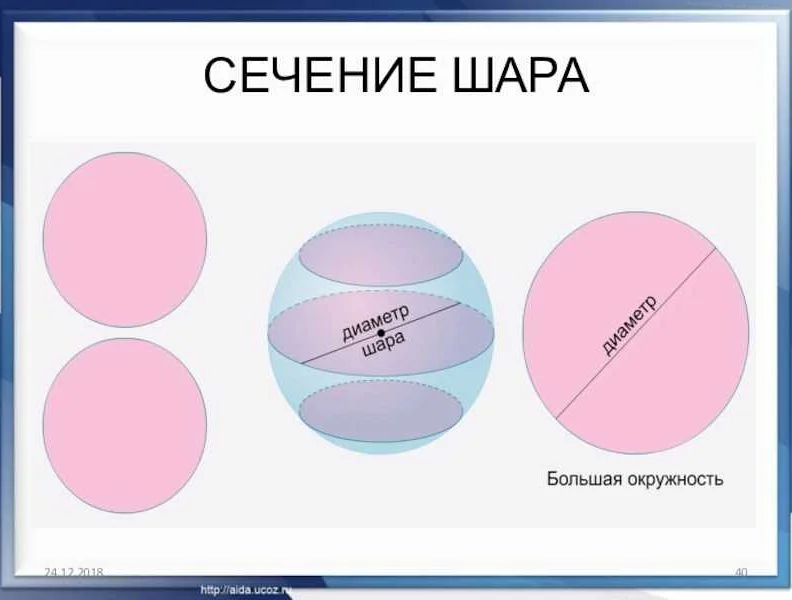
Круглые тела – это тела, у которых поперечное сечение является кругом. Они имеют ряд характеристик, которые определяют их свойства и применения в разных областях математики и физики.
Объём круглых тел. Объём круглых тел можно вычислить с помощью формулы, зависящей от реализации тела. В случае сферы используется формула V = (4/3)πr^3, где r – радиус сферы.
Площадь поверхности круглых тел. Площадь поверхности круглых тел также зависит от конкретной реализации тела. Например, для сферы показательные формулы – S = 4πr^2.
Инерционные характеристики круглых тел. Инерционные характеристики круглых тел, такие как масса, момент инерции и радиус инерции, играют важную роль при решении задач динамики и механики материалов. Они могут быть вычислены с помощью соответствующих формул.
Приложения круглых тел. Круглые тела находят широкое применение в различных областях математики и физики. Например, для решения задач о движении тел в пространстве используются формулы, основанные на характеристиках круглых тел.
Формулы расчета объема круглых тел
Шар:
Объем шара можно рассчитать по формуле: V = (4/3)πr³, где π – математическая константа, приблизительно равная 3,14, а r – радиус шара.
Цилиндр:
Объем цилиндра равен произведению площади основания на высоту: V = S⋅h, где S – площадь основания, а h – высота цилиндра.
Конус:
Объем конуса можно рассчитать по формуле: V = (1/3)S⋅h, где S – площадь основания конуса, а h – высота конуса.
Сфера:
Объем сферы можно рассчитать по формуле: V = (4/3)πr³, где π – математическая константа, приблизительно равная 3,14, а r – радиус сферы.
Как определить площадь поверхности круглых тел
Площадь поверхности круглого тела представляет собой сумму площадей всех его граней. Для определения площади поверхности круглого тела необходимо сначала найти площади всех его граней, а затем сложить их.
Для примера рассмотрим площадь поверхности шара. Шар имеет всего одну грань – его поверхность. Площадь его поверхности можно найти по формуле:
S = 4πr²
где r – радиус шара, а π – математическая константа, равная примерно 3,14.
Площадь поверхности цилиндра можно найти по формуле:
S = 2πrh + 2πr²
где r – радиус основания цилиндра, а h – его высота.
Площадь поверхности конуса можно найти по формуле:
S = πr(r+√(h²+r²))
где r – радиус основания конуса, а h – его высота.
Также можно использовать таблицы для определения площади поверхности круглых тел. В таких таблицах указаны формулы для расчета площадей различных тел.
Общие свойства круглых тел
Круглое тело – это тело, объем которого равен объему шара. Некоторые известные круглые тела: шар, сферический сектор, сферический слой.
Существует несколько важных свойств круглых тел. Во-первых, они обладают симметрией. Это означает, что при повороте вокруг оси находящейся в центре тела, тело остается неизменным.
Во-вторых, у круглых тел есть минимальная поверхность. В случае шара, это сфера, у которой каждая точка находится на одинаковом расстоянии от центра. Это свойство имеет много применений в различных областях, включая архитектуру и инженерное дело.
Также круглые тела имеют максимальную внутреннюю пространственную свободу. То есть, круглые тела имеют максимальный объем при заданной площади поверхности.
Несмотря на то, что круглые тела используются во многих областях, включая физику, химию и математику, они также являются важными для многих практических задач, таких как дизайн упаковки, дизайн зданий, а также живопись и визуальное искусство.
Геометрический смысл круглых тел
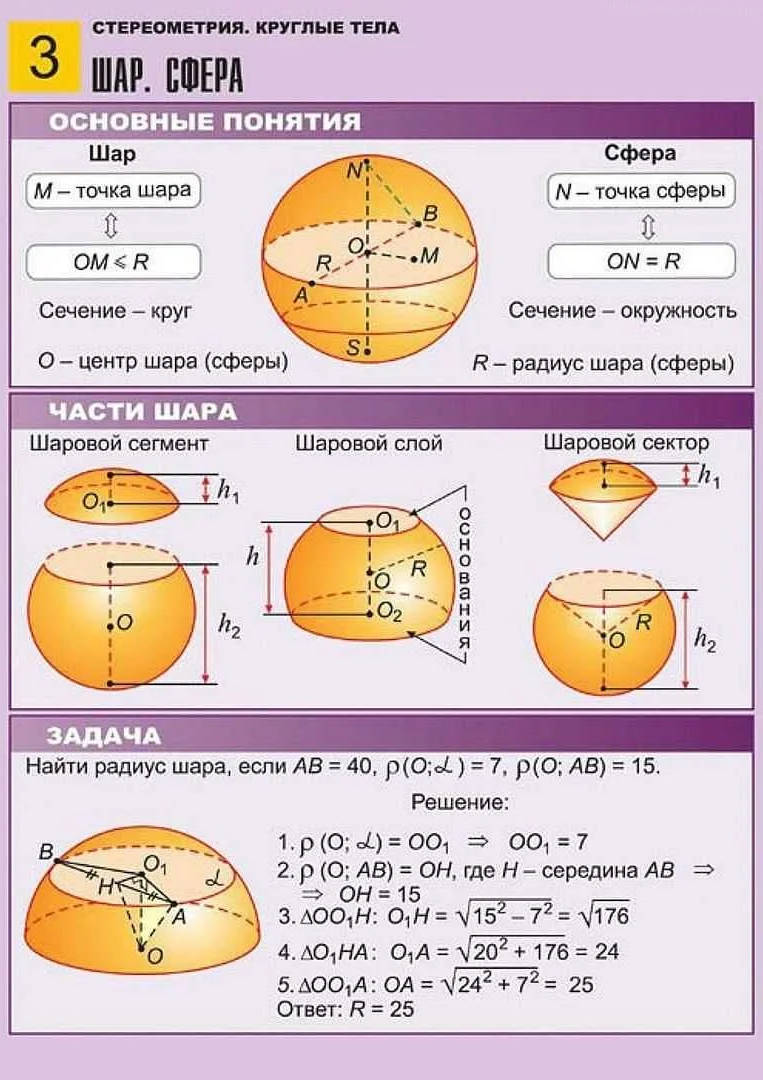
В математике круглые тела являются объектами, имеющими форму сферы, шара, цилиндра или конуса. Эти тела имеют определенные геометрические свойства, которые описываются с помощью различных параметров и характеристик.
Например, радиус и диаметр являются основными параметрами сферы и шара, определяющими размер тела. Высота и радиус основания – параметры цилиндра и конуса. По этим параметрам можно определить другие характеристики круглых тел, такие как объем, площадь поверхности, длина окружности, угол наклона и т.д.
Геометрический смысл круглых тел заключается в том, что они играют важную роль в геометрии и физике, а также в приложениях реального мира. Например, шар используется для определения объема жидкостей или газов, а конусы и цилиндры используются для моделирования трубопроводов, цилиндрических баков и других конструкций.
Круглые тела также являются объектами, которые часто встречаются в природе – кристаллы имеют форму сферы или геометрических фигур, пузыри мыльной воды также имеют форму шаров, а леденцы или конфеты могут иметь форму цилиндров или конусов.
Таким образом, геометрический смысл круглых тел в математике не ограничивается только теорией и абстрактными объектами, но имеет практическое применение в реальном мире.
Примеры использования круглых тел в жизни
Футбольные мячи – это самые популярные круглые тела в мире. Они используются в футболе, самой популярной спортивной игре в мире, которая объединяет миллионы людей по всему миру. Футбольные мячи изготавливаются из кожи, резины и других материалов, и используются в различных условиях – от профессиональных матчей до игр во дворах.
Шары для боулинга – это еще один пример круглых тел, которые используются для развлечения и спорта. Шары для боулинга выпускаются в разных размерах и весах, и использование правильного размера и веса может увеличить шансы на победу в этой игре. Шары для боулинга изготавливаются из полиэстера или других материалов и имеют отверстия для пальцев, чтобы игроки могли удерживать их лучше.
Кулеры – это устройства, которые используют круглые запаянные трубки для охлаждения воды. Кулеры часто используются в качестве источников питьевой воды в офисах, школах и других общественных местах. Вода поступает в кулер, проходит через запаянные трубки, и охлаждается перед тем, как поступить в чашу, где ее можно выпить.
Газовые баллоны – это еще один пример круглых тел, которые имеют важное значение в жизни людей. Газовые баллоны используются для хранения сжатого газа и используются в различных отраслях, включая производство пищевых продуктов, медицинскую технику и сварочное оборудование. Газовые баллоны изготавливают из стали или алюминия и имеют давление в несколько сотен или тысяч фунтов на квадратный дюйм.
Стаканчики для профессионального питания – это круглые тела, которые используются для подачи десертов и других блюд, в которых важно сохранить форму и декоративность. Их используют в профессиональном питании, например на свадьбах и банкетах, а также в кафе и ресторанах, чтобы удивить посетителей интересным дизайном и оригинальностью.
Шары для настольного тенниса – это круглые тела, которые используются в настольном теннисе, который является одним из самых популярных рекреационных видов спорта в мире. Шары для настольного тенниса изготавливаются из пластика или целлюлозы и должны соответствовать определенным стандартам размера и веса, чтобы быть допущены в соревнования.
Кабошоны для ювелирных изделий – это круглые тела, которые используются в ювелирном деле для придания красивого внешнего вида различным украшениям. Кабошоны вырезаются из разных материалов, таких как камни, стекло или синтетические материалы, которые покрываются специальной обработкой, чтобы придать им блеск и яркость. Их используют для изготовления колье, браслетов, сережек и других ювелирных изделий.
Лампы – это еще один пример круглых тел, которые используются повсеместно. Лампы имеют круглую форму и используются в различных типах освещения, от домашнего освещения до освещения улиц и торговых центров. Лампы могут быть сделаны из разных материалов, в зависимости от типа освещения, и иметь разную мощность и яркость.
Таким образом, круглые тела имеют широкое применение в различных сферах жизни – от спорта и развлечений до промышленности и ювелирного деле. Они являются незаменимой частью нашей повседневной жизни и производства, и не перестают удивлять своими различными формами и материалами изготовления.
Вопрос-ответ:
Как определить круглое тело?
Круглое тело – это геометрическое тело, состоящее из точек, равноудаленных от центра. Круглые тела бывают разных форм: сферы, шары, цилиндры, конусы и т.д.
Какие свойства имеют круглые тела?
Основные свойства круглых тел: радиус, диаметр, объем, площадь поверхности и высота. Также для каждого конкретного круглого тела могут быть свои уникальные характеристики.
Какие математические методы применяются для изучения круглых тел?
Для изучения круглых тел применяются различные методы математического анализа: интегралы, дифференциальные уравнения, векторная алгебра и геометрия, аналитическая геометрия и т.д.
Что такое объем круглого тела?
Объем круглого тела – это мера его внутреннего пространства. Для сферы объем можно вычислить по формуле V = 4/3πr^3, для шара – V = 4/3πr^3, для цилиндра – V = πr^2h, для конуса – V = 1/3πr^2h и т.д.
Как вычислить площадь поверхности круглого тела?
Площадь поверхности круглого тела – это сумма всех поверхностей, составляющих это тело. Для сферы площадь поверхности можно вычислить по формуле S = 4πr^2, для шара – S = 4πr^2, для цилиндра – S = 2πrh + 2πr^2, для конуса – S = πrl + πr^2 и т.д.
Какие примеры круглых тел встречаются в реальной жизни?
Примеры круглых тел включают: мячи (футбольные, баскетбольные, теннисные и т.д.), яблоки, оранжевые, шарики для гольфа, шары мира, планеты, капли воды и т.д.
Какая философская концепция связана с круглыми телами?
В философии античности круглое тело было символом совершенства и божественности, так как шар был считается формой, имеющей неограниченность и неразрывность. Также круглые тела очень часто использовались в магических обрядах и ритуалах.






