Квадратный сантиметр – это единица площади, которую изучают дети в 3 классе математики. В данной статье мы расскажем, что такое квадратные сантиметры, как их измерять и зачем это нужно знать. Пригодится как школьникам, так и их родителям в современном мире, где математика занимает прочное место!
Квадратные сантиметры – это единица измерения площади, которая используется в математике. В 3 классе, дети начинают изучать основные понятия геометрии, включая понятие площади. Площадь – это мера поверхности фигуры. Квадратные сантиметры помогают измерить площадь в квадратных сантиметрах.
Для того, чтобы прочувствовать, что такое квадратные сантиметры, можно представить простую ситуацию. Возьмем лист бумаги и измерим его длину и ширину с помощью линейки. Умножим эти два числа друг на друга и получим площадь листа бумаги в квадратных сантиметрах. Если лист бумаги имеет длину 20 сантиметров и ширину 15 сантиметров, то его площадь будет равна 300 квадратных сантиметров.
Далее, в 3 классе дети начинают изучать фигуры с помощью которых можно учиться измерять площадь. Это могут быть квадраты, прямоугольники, треугольники и другие фигуры. Квадратные сантиметры помогают изучать площадь фигур и решать задачи, связанные с этой темой.
Определение квадратных сантиметров
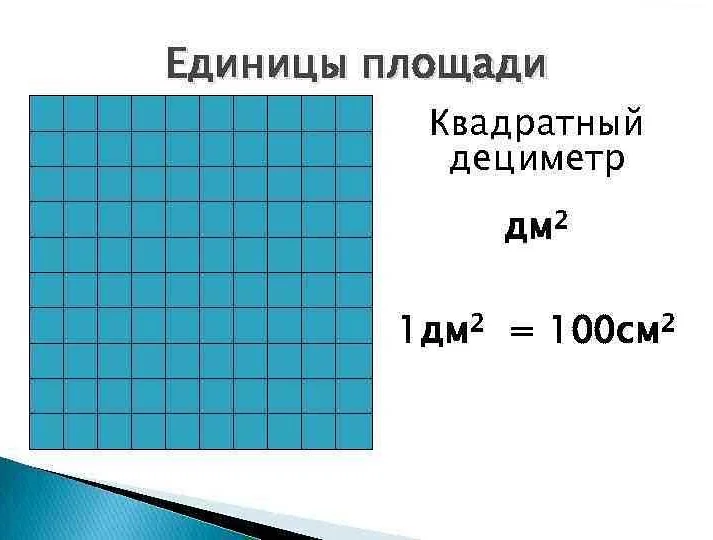
Квадратные сантиметры – это мера площади. Когда мы говорим о площади, мы говорим о том, сколько места занимает объект на плоскости. Измерять площадь можно разными единицами, но одной из наиболее удобных является квадратный сантиметр.
Квадратный сантиметр представляет собой квадрат со стороной в один сантиметр. Таким образом, квадратный сантиметр имеет площадь один квадратный сантиметр. Его обозначают с помощью сокращения “см²”.
Для измерения площади объекта мы считаем количество квадратных сантиметров, которые занимает этот объект на плоскости. Например, если мы хотим измерить площадь стола, мы можем разбить его на квадраты со стороной в один сантиметр и посчитать количество этих квадратов. Полученное число и будет показателем площади стола в квадратных сантиметрах.
Знание квадратных сантиметров помогает нам понимать, насколько большой или маленькой является площадь объекта. Это важно не только для математических расчетов, но и для повседневного использования, например, при выборе размеров ковра или площади комнаты.
Измерение площади
Площадь – это количество поверхности, которую занимает фигура. Для измерения площади используется различные единицы измерения, например, квадратные сантиметры, квадратные метры, квадратные футы и т.д.
Для расчета площади прямоугольника необходимо умножить длину на ширину. Например, если длина прямоугольника равна 4 см, а его ширина – 3 см, то общая площадь составит 12 квадратных сантиметров.
Для особенных фигур существует свой метод расчета площади. Так, площадь треугольника можно рассчитать по формуле «1/2 * основание * высота», а площадь круга – по формуле «π * радиус²».
В школьной программе, как правило, рассматриваются простые фигуры, к которым применяются основные методы измерения площади. Ученики должны уметь расчитывать площадь прямоугольника, квадрата и треугольника, а также уметь сравнивать их между собой.
- Применение в жизни: понимание измерения площади является важным навыком во многих сферах жизни, начиная от строительства и кончая земельным правом;
- Развитие логики: измерение площади позволяет развивать у детей логическое мышление и умение анализировать информацию;
- Практическая польза: умение расчитывать площадь помогает в жизни решить множество практических задач, например, количества краски для окрашивания стен в комнате;
- Подготовка к более сложным задачам: понимание основных принципов измерения площади является важной подготовкой к более сложным вычислениям на более продвинутых этапах обучения.
Формула для нахождения площади квадрата
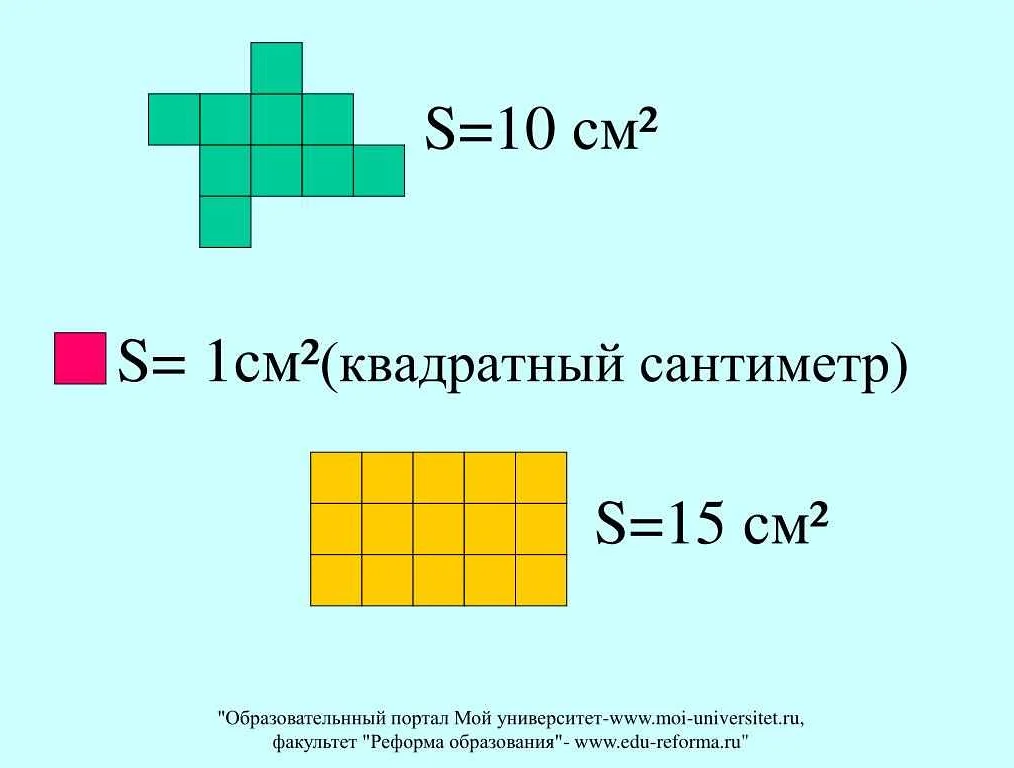
Квадрат – это фигура, которая имеет четыре равные стороны и четыре прямых угла. Площадь квадрата – это количество площади, занимаемой данной фигурой.
Формула для нахождения площади квадрата очень простая. Нужно умножить длину одной стороны на себя. Таким образом, если нам дана сторона квадрата длиной 5 см, мы можем найти его площадь, используя следующую формулу:
Площадь квадрата = сторона × сторона
В данном случае:
- сторона = 5 см
- площадь квадрата = 5 × 5 = 25 квадратных сантиметров
Таким образом, площадь квадрата можно найти, зная длину любой его стороны. Это очень полезная формула, которая поможет вам в решении задач в школе и в жизни.
Практические задачи на нахождение площади квадрата
Принцип нахождения площади квадрата прост: сначала нужно измерить длину стороны квадрата, а затем возвести ее в квадрат.
Например, если сторона квадрата равна 5 сантиметров, то его площадь равна 25 квадратным сантиметрам (5 × 5 = 25).
Вот несколько практических задач на нахождение площади квадрата:
- Найдите площадь квадрата со стороной 8 сантиметров.
- Если площадь квадрата равна 36 квадратным сантиметрам, какова длина его стороны?
- У квадрата сторона равна 12 сантиметров. Найдите его площадь.
Для нахождения ответа на каждую задачу нужно использовать принцип, описанный выше. Вы можете использовать таблицу для записи решения каждой задачи.
ЗадачаРешениеОтвет
| № 1 | 8 × 8 = 64 | Площадь равна 64 квадратным сантиметрам |
| № 2 | √36 = 6 | Сторона равна 6 сантиметрам |
| № 3 | 12 × 12 = 144 | Площадь равна 144 квадратным сантиметрам |
Таким образом, нахождение площади квадрата – это простой и важный математический навык, который позволяет решать множество задач в повседневной жизни.
Формула для нахождения площади прямоугольника
Площадь прямоугольника – это показатель, выражающий понятие площади фигуры, образованной четырьмя прямыми линиями. Она равна произведению длины и ширины прямоугольника.
Формула для нахождения площади прямоугольника: S = a * b, где S – площадь, а и b – длины сторон прямоугольника.
Эту формулу можно просто запомнить и применять в любой ситуации. Например, если нам даны значения длины и ширины прямоугольника, мы можем вычислить его площадь, используя эту формулу.
Имея понимание о том, что такое квадратные сантиметры, можно легко рассчитать площадь прямоугольника в данной единице измерения. Например, если длина и ширина прямоугольника равны соответственно 5 см и 6 см, то его площадь будет равна 30 квадратным сантиметрам.
Практические задачи на нахождение площади прямоугольника
Задача 1: У Антона есть прямоугольный участок земли длиной 15 метров и шириной 8 метров. Найдите площадь участка земли.
Решение: Площадь прямоугольника находится по формуле:
S = a * b
где S – площадь прямоугольника, a – длина прямоугольника, b – ширина прямоугольника.
Подставляем значения из задачи: S = 15 м * 8 м = 120 квадратных метров.
Задача 2: Матвей решил покрасить свою комнату, которая имеет форму прямоугольника. Длина комнаты 6 метров, а ширина 4 метра. Сколько квадратных метров нужно закрасить, если на один квадратный метр придется 1 литр краски.
Решение: Нужно найти площадь комнаты и узнать, сколько литров краски потребуется. Площадь комнаты находим по формуле:
S = a * b
где S – площадь прямоугольника, a – длина комнаты, b – ширина комнаты.
Подставляем значения из задачи: S = 6 м * 4 м = 24 квадратных метра.
Значит, для закраски комнаты нужно 24 литра краски.
Задача 3: Вася увлекается выращиванием овощей на даче. Он замерил грядку, которая имеет форму прямоугольника, длиной 8 метров и шириной 2 метра. Найдите площадь грядки.
Решение: Площадь грядки находим по формуле:
S = a * b
где S – площадь прямоугольника, a – длина грядки, b – ширина грядки.
Подставляем значения из задачи: S = 8 м * 2 м = 16 квадратных метров.
Задачи на нахождение площади квадрата и прямоугольника
Площадь фигуры – это понятие, которое обозначает количество площади той поверхности, которую занимает эта фигура. Найдем площадь квадрата и прямоугольника.
Задача 1: Найдите площадь квадрата со стороной 5 см.
Решение: Для определения площади квадрата нужно умножить значение длины его стороны на саму себя. Так как у нас квадрат со стороной 5 см, то его площадь равна:
5 см x 5 см = 25 квадратных сантиметров.
Ответ: Площадь квадрата со стороной 5 см равна 25 квадратных сантиметров.
Задача 2: Найдите площадь прямоугольника со сторонами 6 см и 8 см.
Решение: Для определения площади прямоугольника нужно умножить значение длины его сторон. Так как у нас прямоугольник с длиной 6 см и шириной 8 см, то его площадь равна:
6 см x 8 см = 48 квадратных сантиметров.
Ответ: Площадь прямоугольника со сторонами 6 см и 8 см равна 48 квадратных сантиметров.
Теперь вы знаете, как находить площадь квадрата и прямоугольника. Помните, что площадь измеряется в квадратных единицах.
Формула для нахождения площади треугольника
Площадь треугольника – это одна из важнейших величин в геометрии. Она позволяет нам определить, сколько площади занимает треугольная фигура на плоскости.
Формула для нахождения площади треугольника выглядит следующим образом:
S = 1/2 * a * h
где S – это площадь, a – это длина основания треугольника, а h – это высота, опущенная из вершины на основание.
Для того чтобы применить эту формулу, необходимо знать длину основания и высоту треугольника. Длину основания можно измерить с помощью линейки, а высоту можно найти, проведя перпендикуляр от вершины до основания.
Также существуют другие способы нахождения площади треугольника, например, с помощью формулы Герона, если известны длины всех трех сторон. Но формула с высотой и основанием является самой простой и удобной для использования.
Практические задачи на нахождение площади треугольника
Решение задач по нахождению площади треугольника является важным элементом обучения математике в начальной школе. Необходимо понимать, как правильно рассчитать площадь треугольника и как применить полученные знания на практике.
Одна из задач заключается в определении площади равнобедренного треугольника. Для этого нужно найти высоту, проведенную к основанию, затем умножить основание на высоту и разделить полученный результат пополам.
Другая задача состоит в нахождении площади прямоугольного треугольника. В данном случае необходимо умножить длину одного катета на длину другого катета и разделить полученный результат пополам.
Третья задача – определение площади произвольного треугольника. Для этого требуется знать длины всех трех сторон. По формуле Герона можно вычислить площадь, зная все стороны треугольника. Сначала нужно найти полупериметр – сумму длин всех сторон, разделенную на 2, затем использовать этот результат для вычисления площади по формуле Герона.
Учитывая все вышеперечисленные задачи, можно заключить, что нахождение площади треугольника – важный компонент в обучении математике в начальной школе. Это помогает развивать логическое мышление, приобретать умения решения практических задач и применять полученные знания на практике.
Задачи на нахождение площади фигур из нескольких простых фигур
В математике часто бывает нужно найти площадь фигуры, состоящей из нескольких простых фигур. Для этого необходимо знать формулы нахождения площади простых фигур: квадрата, прямоугольника, треугольника и круга.
Например, для нахождения площади прямоугольника нужно умножить его длину на ширину: S = a * b. А для нахождения площади круга нужно возвести радиус в квадрат и умножить на число пи (π): S = π * r².
Задачи на нахождение площади фигур из нескольких простых фигур могут быть самыми разными. Например, нужно найти площадь фигуры, состоящей из трех треугольников и квадрата. Для этого нужно сначала найти площади каждого из этих простых фигур, а затем сложить их: S = Sквадрата + Sтреугольника 1 + Sтреугольника 2 + Sтреугольника 3.
Чтобы решить задачу на нахождение площади фигуры из нескольких простых фигур, нужно использовать знания о формулах площади простых фигур и умение складывать числа. Такие задачи помогают развивать логическое мышление и способность анализировать сложные ситуации.
- Пример задачи: Найди площадь фигуры, состоящей из прямоугольника и круга.
- Решение: Сначала найдем площадь прямоугольника, умножив его длину и ширину: Sпрямоугольника = 6 * 4 = 24. Затем найдем площадь круга, используя формулу площади круга: Sкруга = π * 3² = 28,27. И, наконец, сложим эти площади: S = Sпрямоугольника + Sкруга = 24 + 28,27 = 52,27.
Вопрос-ответ:
Что такое квадратные сантиметры?
Квадратные сантиметры – это единица измерения площади в системе метрических единиц. Один квадратный сантиметр – это площадь квадрата со стороной равной одному сантиметру.
Для чего нужны квадратные сантиметры в 3 классе математики?
В 3 классе математики квадратные сантиметры используются для изучения понятия площади. Дети учатся находить площадь прямоугольника, квадрата, а также различных фигур на сетке.
Как правильно измерять площадь?
Площадь измеряется в квадратных единицах измерения, например, квадратных сантиметрах. Для нахождения площади прямоугольника необходимо умножить длину на ширину. Для квадрата, достаточно возвести в квадрат длину стороны.
Как находить площадь фигур на сетке?
Для нахождения площади фигур на сетке нужно знать количество квадратных клеточек, которые занимает фигура. Например, для нахождения площади треугольника на сетке, нужно поделить треугольник на прямоугольники из клеточек и сложить площади этих прямоугольников.
Какие еще единицы измерения площади существуют?
Единицы измерения площади, помимо квадратных сантиметров, могут быть квадратными метрами, квадратными миллиметрами, квадратными километрами и др. Каждая из этих единиц измерения соответствует своей площади.
Как находить площадь круга?
Площадь круга вычисляется по формуле: S = πr², где S – площадь круга, π – число пи (отношение длины окружности к диаметру), r – радиус круга.
Зачем нужно изучать понятие площади?
Понятие площади широко используется в нашей повседневной жизни и в различных областях науки и техники. Изучение площади помогает детям лучше понять отношения и масштабы, а также развивает логическое мышление и умение решать задачи.
Примеры задач на нахождение площади, используя все формулы
1. Найдем площадь прямоугольника, у которого стороны равны 6 см и 8 см.
Формула для нахождения площади прямоугольника:
S = a * b
где a и b – длины сторон.
Подставляем значения в формулу:
S = 6 см * 8 см = 48 см²
Ответ: площадь прямоугольника равна 48 квадратным сантиметрам.
2. Найдем площадь квадрата со стороной 5 см.
Формула для нахождения площади квадрата:
S = a²
где a – длина стороны.
Подставляем значение в формулу:
S = 5 см * 5 см = 25 см²
Ответ: площадь квадрата равна 25 квадратным сантиметрам.
3. Найдем площадь треугольника, у которого основание равно 10 см, а высота 6 см.
Формула для нахождения площади треугольника:
S = 1/2 * a * h
где a – длина основания, h – высота треугольника.
Подставляем значения в формулу:
S = 1/2 * 10 см * 6 см = 30 см²
Ответ: площадь треугольника равна 30 квадратным сантиметрам.
4. Найдем площадь трапеции, у которой верхнее основание равно 8 см, нижнее основание – 12 см, а высота – 4 см.
Формула для нахождения площади трапеции:
S = 1/2 * (a + b) * h
где a и b – длины верхнего и нижнего оснований соответственно, h – высота трапеции.
Подставляем значения в формулу:
S = 1/2 * (8 см + 12 см) * 4 см = 40 см²
Ответ: площадь трапеции равна 40 квадратным сантиметрам.






