LM – это сокращение от Linear Model (линейная модель), статистического метода, используемого в математическом анализе данных для описания и прогнозирования зависимостей между переменными. Узнайте, как работает LM и какие применения у этого метода.
В математике существует множество терминов и обозначений, которые могут показаться непонятными для новичков или просто людей, не знакомых с этой наукой. В частности, многие могут столкнуться с обозначением lm, которое часто используется в статистике и анализе данных.
Кратко говоря, lm означает линейную регрессию, которая используется для построения модели связи между двумя переменными величинами. Примерами могут служить связь между температурой и количеством продаж мороженого или же связь между количеством часов, посвященных учебе, и оценками студентов.
Построение модели связи между переменными является важным инструментом анализа данных и может быть полезным для многих областей, начиная от бизнеса до научных исследований. Использование lm позволяет не только определить наличие связи между переменными, но и предсказать значения одной перменной на основе значений другой.
Определение линейной модели
Линейная модель (LM) – это математическая модель, используемая в статистике, которая описывает связь между зависимой переменной и одной или несколькими независимыми переменными. Его основное свойство – это линейная зависимость между зависимой переменной и независимой переменной.
Данные модели могут быть использованы в различных областях, таких как экономика, бизнес, физика, инженерия и т.д. Они могут использоваться для прогнозирования будущих значений, обнаружения взаимосвязей, оценки вестибулярного эффекта и так далее.
В линейной модели независимой переменной называется регрессором, а зависимой переменной – регрессантом. В модели может присутствовать несколько регрессоров, которые могут иметь линейную, квадратичную или другую нелинейную зависимость с регрессантом.
Одним из важных аспектов линейной модели является выбор наилучшей модели, которая наиболее точно предсказывает данные и имеет лучшую экспланаторную способность. Этот выбор может основываться на статистических критериях, таких как MSE, R-квадрат, AIC, BIC и другие.
Видео по теме:
Как работает lm в математике
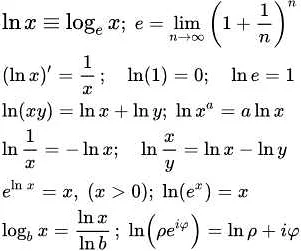
lm (линейная регрессия) – это статистический алгоритм, который используется для описания и анализа связи между двумя переменными. Этот алгоритм особенно полезен в анализе экономических и финансовых прогнозов, а также в исследованиях социальных наук и медицины.
В линейной регрессии lm модель строится путем поиска наилучшей прямой (линейной) зависимости между двумя переменными. Эта прямая обеспечивает наилучшую подгонку данных и может быть использована для предсказания значений зависимой переменной на основе известных значений независимой переменной.
Алгоритм lm использует метод наименьших квадратов (OLS), чтобы минимизировать разницу между фактическими и предсказанными значениями зависимой переменной. Этот метод наименьших квадратов определяет линейную функцию, которая наилучшим образом соответствует данным, и на основе этой функции определяется коэффициент r^2, который показывает насколько хорошо модель соответствует данным.
Важно отметить, что линейная регрессия lm не подходит для анализа нелинейных зависимостей между переменными, а также не гарантирует причинно-следственную связь между переменными. Она лишь помогает описать и анализировать корреляцию между переменными и на основе этой корреляции предсказывать значения зависимой переменной.
В заключение, линейная регрессия lm – это мощный инструмент статистического анализа, который позволяет строить модели, описывающие взаимосвязь между парами переменных. Однако для правильного использования этого инструмента важно иметь хорошее понимание статистических методов и умение интерпретировать результаты.
Зачем нужно использовать lm в математике
Lineal model (lm) – это тип регрессионного анализа, который используется в математике для описания связи между наблюдаемыми данными. Он может быть использован для выявления зависимостей между различными переменными, а также для прогнозирования будущих значений на основе известных данных.
Одним из главных преимуществ использования lm в математике является то, что он позволяет исследовать отношения между несколькими переменными одновременно. Он может быть использован для анализа комплексных данных, которые могут быть сложными для понимания и интерпретации с помощью других методов.
Кроме того, lm является ресурсосберегающим методом анализа данных. Он позволяет получить высокую точность прогнозов при ограниченных ресурсах, что делает его привлекательным выбором для исследователей и бизнесменов.
Поэтому, использование lm в математике может помочь в принятии лучших решений, улучшении производительности и достижении более точных прогнозов в различных областях, таких как экономика, финансы, наука и технологии.
И, наконец, необходимым условием для правильного использования lm в математике является математическая подготовка специалистов, что делает его наиболее эффективным при работе со специалистами в этой области.
Вопрос-ответ:
Что такое lm в математике?
LM (англ. linear model) — линейная модель, используемая в статистике для анализа и представления зависимости между переменными.
Какие примеры применения LM в математике?
Примерами применения LM могут быть: анализ зависимости зарплаты от опыта работы и уровня образования; анализ влияния факторов (выпуск продукции, рекламный бюджет, цены на рынке) на прибыль компании.
Как вычисляются коэффициенты линейной модели?
Коэффициенты линейной модели вычисляются методом наименьших квадратов (МНК), который минимизирует сумму квадратов остатков между фактическими значениями переменных и их модельными значениями.
Какие ограничения есть у линейной модели?
Линейная модель предполагает линейную зависимость между переменными, отсутствие мультиколлинеарности между факторами, гомоскедастичность и нормальность остатков.
Чем отличается простая линейная регрессия от множественной?
Простая линейная регрессия анализирует зависимость между двумя переменными, в то время как множественная линейная регрессия позволяет учитывать влияние нескольких факторов на исследуемую переменную.
В каких программах можно проводить анализ линейной модели?
Анализ линейной модели можно проводить во многих программных пакетах, таких как R, Python, SPSS, Stata, SAS и др.
Как интерпретировать коэффициенты линейной модели?
Каждый коэффициент линейной модели указывает на изменение зависимой переменной при изменении соответствующей независимой переменной на единицу, при условии, что остальные переменные не меняются.
Основные свойства lm в математике
lm — это сокращение от английского словосочетания linear model, по-русски это означает линейную модель. Она представляет собой статистический метод для изучения связи между различными переменными. В основном, lm используется в эконометрике, где он используется для анализа экономических данных.
Основные свойства lm следующие:
- Линейность – модель строится на предположении, что зависимая переменная и независимые переменные имеют линейную связь. Это означает, что график отображает прямую линию, что упрощает анализ данных и экономических выводов;
- Независимость ошибок – ошибки в модели должны быть случайными и независимыми между собой;
- Гомоскедастичность – ошибка должна иметь постоянную дисперсию во всех уровнях независимых переменных, что позволяет оценить степень изменчивости результатов;
- Нормальность – ошибка должна распределена нормально, что помогает в определении значимости результатов модели.
В результате использования метода линейной модели, экономисты и исследователи могут получить ценную информацию об отношении независимых переменных к зависимым переменным. Это может помочь предсказывать будущие результаты и принимать эффективные решения в различных областях, таких как экономика, финансы и бизнес.
Примеры применения lm в математике
Метод линейной регрессии (lm) является одним из наиболее распространенных и простых способов моделирования в математике. В частности, он часто используется для прогнозирования результатов экспериментов и исследований.
Например, можно использовать lm для построения модели зависимости между размером популяции и количеством продукции. Это может быть полезно для определения оптимального размера производства в зависимости от количества потребности рынка, а также для прогнозирования будущих продаж на основе текущих данных.
Другой пример использования lm в математике – построение моделей прогнозирования цен на акции и другие финансовые инструменты на основе текущих исторических данных. По сути, lm позволяет определить, какие факторы могут влиять на цену и как значение каждого из них может изменяться в будущем.
Также метод линейной регрессии можно использовать для анализа влияния факторов на здоровье человека. Например, можно определить, какие факторы повышают риск заболевания сердечно-сосудистой системы, и какие лекарства или процедуры могут снижать этот риск.
В целом, использование lm позволяет установить закономерности между различными переменными, что может быть полезно для принятия решений и определения оптимальных стратегий в различных областях деятельности.
Как создать lm модель

Линейная регрессия является одним из наиболее распространенных методов статистического моделирования. Для создания lm модели необходимо выполнить следующие шаги:
- Подготовить данные: собрать данные и подготовить их к использованию в R. Данные могут быть представлены в виде таблиц или списков.
- Загрузить библиотеку: для работы с lm моделью в R необходимо загрузить библиотеку “stats”. Это можно сделать с помощью команды library(stats).
- Построить модель: с помощью функции lm() можно построить модель. Например, lm(y ~ x1 + x2) построит модель с зависимой переменной y и двумя независимыми переменными x1 и x2.
- Анализировать результаты: после построения модели необходимо проанализировать результаты и определить, насколько хорошо модель соответствует данным. Для этого можно использовать различные метрики, такие как коэффициент детерминации (R-квадрат).
Хорошо подобранная lm модель может помочь сделать предсказания о поведении данных в будущем и принимать более эффективные решения.
Интерпретация lm модели
Чтобы правильно интерпретировать результаты lm модели, необходимо понимать, какие переменные были включены в модель и какие коэффициенты регрессии получились после обучения модели.
Каждый коэффициент регрессии отражает влияние соответствующей переменной на зависимую переменную в модели. Знак коэффициента указывает на направление этого влияния: положительный знак означает прямую зависимость, отрицательный – обратную. Абсолютное значение коэффициента указывает на силу влияния переменной на зависимую переменную в единицах измерения.
Кроме того, необходимо обратить внимание на значимость коэффициентов. Коэффициент считается значимым, если его p-значение меньше уровня значимости (обычно принимается равным 0.05). Если коэффициент не значим, то его влияние на зависимую переменную можно считать незначительным и не существенным.
Важно помнить, что lm модель описывает только линейную зависимость между переменными, поэтому если в данных присутствует нелинейность, интерпретация результатов может быть неправильной.
В целом, интерпретация lm модели требует внимательности и аккуратности, так как неправильное объяснение результатов может привести к неверным выводам и даже к ошибкам в принятии решений.
Как проводить статистические тесты для lm модели
lm модель – это математическая модель, которая используется для прогнозирования значения зависимой переменной на основе значений одной или нескольких независимых переменных. Чтобы проверить, насколько хорошо lm модель объясняет зависимость между переменными, проводят статистические тесты.
Тест F по ANOVA таблице
Первым шагом в проведении статистических тестов является ANOVA таблица, которая показывает, насколько хорошо модель описывает данные. Для этого используются тесты F в ANOVA таблице. Они сравнивают объясненную и необъясненную дисперсии между группами и позволяют определить, есть ли значимые различия между группами.
Тест t для проверки значимости коэффициентов
Для проверки значимости каждого из коэффициентов в lm модели используется t-тест. Он определяет, является ли оценка коэффициента значимой. Критические значения t-статистики зависят от числа степеней свободы и уровня значимости. Если t-значение соответствует p-уровню значимости меньше, чем заданный уровень значимости (обычно 0,05), то коэффициент считается значимым.
Тест R-квадрат для определения объяснительной способности модели
Чтобы оценить, насколько хорошо lm модель подходит для данных, используется тест R-квадрат. Этот тест определяет, какой процент изменчивости переменной зависимости можно объяснить переменными, используемыми в модели. Чем выше значение R-квадрат, тем лучше модель подходит для данных.
Оценка остатков
Еще одним способом проверки точности lm модели является анализ остатков. Остатки – это разница между фактическими значениями зависимой переменной и предсказанными значениями, полученными с помощью модели. Анализ остатков позволяет определить, есть ли какие-либо неустранимые ошибки в модели. Например, если остатки распределены неравномерно, то может быть необходимо изменить модель для улучшения точности предсказания.
Какие ошибки могут возникать при использовании lm в математике
1. Неверно заданные данные: Наиболее распространенной ошибкой при использовании lm является неверно заданные данные, например, неправильно указанные переменные или неправильно прочитанные числа. Такие ошибки могут привести к некорректным результатам.
2. Нарушение предположений о данных: lm, как и любой другой метод, имеет определенные предположения о данных. Если эти предположения нарушены, результаты могут быть неточными или несостоятельными. Например, если данные не проходят проверку на нормальность, то часто возникают проблемы.
3. Проблемы с мультиколлинеарностью: Мультиколлинеарность – это проблема, когда одна или несколько переменных в модели линейно связаны друг с другом. В этом случае lm может дать неверные или неточные результаты. Эта проблема возникает, когда в модели присутствует большое количество переменных или когда эти переменные имеют очень высокую степень корреляции друг с другом.
4. Проблемы с выбросами: Если в данных присутствуют выбросы, то результаты могут быть неточными или искаженными. lm считается чувствительным к выбросам, и поэтому очень важно корректно обрабатывать такие значения.
5. Недостаточная выборка: Другой распространенной ошибкой является недостаточный объем выборки, то есть слишком маленькое количество данных для корректной оценки модели. В этом случае lm может не дать надежных результатов, и требуется использовать другие методы, например, регрессию.
Несмотря на то, что lm является одним из наиболее распространенных методов регрессии, он имеет определенные ограничения и предположения относительно данных. Поэтому для получения точных результатов необходимо уделять должное внимание корректному выбору переменных, правильной обработке данных, а также использованию других методов, если lm не подходит.
Сравнение lm с другими моделями в математике
Линейная регрессия, также известная как модель lm, является одним из наиболее широко используемых в математике способов представления связи между двумя переменными. В отличие от некоторых других моделей, lm основана на представлении отношений между переменными как линейной функции, что означает, что изменение одной переменной будет приводить к пропорциональному изменению другой переменной.
Сравнительный анализ lm с другими моделями показывает, что, поскольку она работает только с линейными отношениями, она может быть менее точной, когда отношения между переменными нелинейные. Например, если отношение между двумя переменными имеет форму U, то линейная регрессия может дать менее точные результаты, чем другие модели, которые могут аппроксимировать нелинейную кривую.
Однако, lm может быть полезной, когда отношение между переменными линейное, которым обладает большое число взаимосвязей в экономических, научных и социологических исследованиях. Кроме того, поскольку lm быстро и просто вычисляется компьютером, она может быть более практичной для анализа данных, чем более сложные модели, когда точность не требуется на высоком уровне.
В итоге, lm может быть важным инструментом для анализа данных при наличии линейного отношения между переменными. Однако, при работе с данными, где отношения между переменными нелинейные, рекомендуется использовать другие модели.
Возможные дальнейшие исследования lm в математике
1. Расширение модели lm
Модель lm – это один из самых простых методов для описания связи между зависимой и независимыми переменными. Однако, он может быть неприменим к сложным ситуациям, когда имеются нелинейные зависимости, выбросы и выборки с пропущенными значениями. Дальнейшие исследования могут направляться на разработку расширенных моделей lm, которые учтут эти факторы.
2. Применение lm в машинном обучении
Метод lm может быть применен в машинном обучении для задач регрессии. Однако, дальнейшие исследования могут направляться на исследование его возможностей в задачах классификации и кластеризации.
3. Оптимизация модели lm
Метод lm можно оптимизировать, чтобы он имел лучшую точность предсказаний. Возможные направления – улучшение выбора признаков, уменьшение ошибки выборки, использование более сложных статистических методов.
4. Исследование устойчивости lm
Метод lm может быть чувствителен к выбросам в данных, что может приводить к сильному искажению результатов. Дальнейшие исследования могут направляться на исследование устойчивости lm к выбросам и разработку методов для уменьшения их влияния.
5. Сравнение lm с другими методами регрессии
Существует множество других методов регрессии, имеющих свои преимущества и недостатки. Дальнейшие исследования могут направляться на сравнение метода lm с другими методами регрессии и выбор лучшей модели для конкретных задач.






