Что такое нод в математике 5 класс определение

Главная » Медицина » Нод в математике 5 класс: определение и примеры вычисления

15.08.2023

На чтение: 11 мин.

Нод (наибольший общий делитель) — это наибольшее целое число, которое одновременно является делителем двух или более других целых чисел. В данной статье мы рассмотрим определение нод в математике для учеников 5 класса и приведем примеры его вычисления.

НОД, или наибольший общий делитель, является одной из базовых математических тем, которую изучают в 5 классе. Наибольший общий делитель двух чисел — это наибольшее число, на которое оба числа делятся без остатка. Например, НОД (4, 6) равен 2, потому что 2 является наибольшим числом, которое делится на оба числа 4 и 6 без остатка.

Применение НОДа может быть особенно полезно при работе с дробями. Изучение НОДа также может помочь с пониманием простых чисел и их связи с произведением.

НОД легко можно вычислить при помощи алгоритма Евклида, который состоит из последовательного вычитания одного числа из другого и повторения этой операции до тех пор, пока числа не станут равными. Результат будет наибольшим общим делителем изначальных чисел.

Определение понятия нод

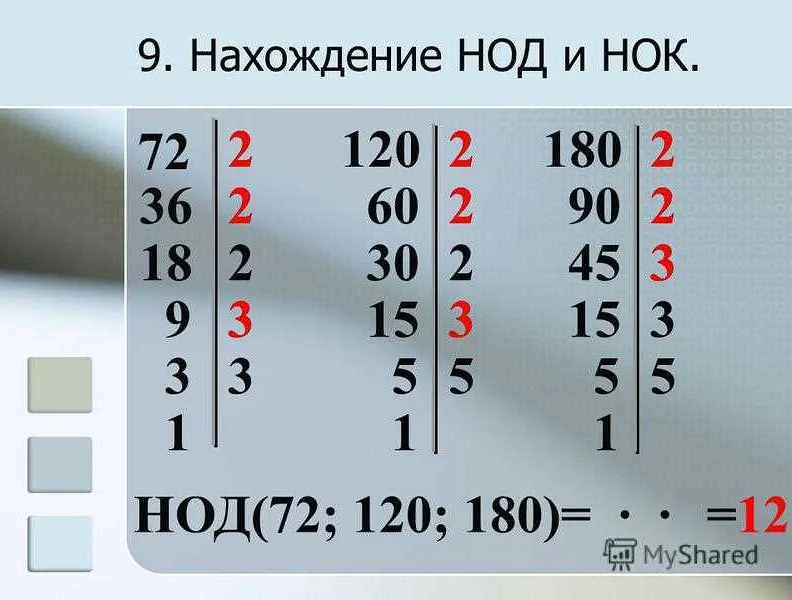
Нод (наибольший общий делитель) — это наибольшее число, которое делит два или несколько чисел без остатка. То есть, если мы имеем два числа, то наибольший общий делитель — это наибольшее число, которое делит оба этих числа без остатка.

Одним из примеров, где может понадобиться знание понятия нод, является упрощение обыкновенных дробей. Для этого нужно найти наибольший общий делитель числителя и знаменателя, и разделить оба числа на него. Таким образом, мы получим дробь, которую нельзя сократить.

Другой важный пример, который связан с понятием нод, — это поиск наименьшего общего кратного двух или нескольких чисел. Наименьшее общее кратное (НОК) — это наименьшее число, которое делится на все заданные числа без остатка. Нок можно найти, зная нод исходных чисел. Для этого нужно умножить числа на их отношение к ноду.

Нод является важным понятием в математике, которое часто используется в различных областях, включая геометрию, вычислительную математику и теорию чисел. Знание понятия нод поможет решать различные задачи, связанные с дробями, делимостью и многими другими математическими проблемами.

Различия между нод и НОК

НОК (наименьшее общее кратное) и НОД (наибольший общий делитель) — две важные математические концепции, которые используются для работы с числами. Однако, эти два понятия имеют различные функции и применяются в разных областях математики.

НОК — это наименьшее число, которое делится на два или более чисел, без остатка. Например, наименьшее число, которое делится без остатка на 4 и 6, это 12.

НОД — это наибольшее число, которое делит два или более чисел, без остатка. Например, наибольший общий делитель чисел 12 и 18 — это 6.

Различия между НОК и НОД:

НОК используется, когда необходимо найти общие кратные чисел, например, в расчетах времени или в работе с дробями.
НОД используется, когда необходимо найти наибольший общий делитель двух или более чисел, например, в упрощении дробей или при решении уравнений.
НОК всегда больше, чем любое из чисел, которые он делит, тогда как НОД всегда меньше или равен любому из чисел, которые он делит.
НОД может быть единственным, тогда как НОК может быть не единственным и существуют разные способы нахождения НОК.

Таким образом, НОК и НОД — это два важных концепта математики, которые можно использовать для решения многих задач, но при этом они различаются по своей сути и применяются в разных областях.

Примеры вычисления нод

НОД двух чисел можно вычислить с помощью метода Эвклида. Этот метод заключается в том, чтобы повторять деление большего числа на меньшее до тех пор, пока остаток не будет равен нулю.

Рассмотрим пример: найдем наибольший общий делитель чисел 24 и 36.

36 ÷ 24 = 1 (остаток 12)
24 ÷ 12 = 2 (остаток 0)

Таким образом, НОД(24, 36) = 12.

Другой пример: найдем НОД чисел 15 и 25.

25 ÷ 15 = 1 (остаток 10)
15 ÷ 10 = 1 (остаток 5)
10 ÷ 5 = 2 (остаток 0)

Таким образом, НОД(15, 25) = 5.

Еще один пример: найдем НОД чисел 36 и 48.

48 ÷ 36 = 1 (остаток 12)
36 ÷ 12 = 3 (остаток 0)

Таким образом, НОД(36, 48) = 12.

Метод Эвклида можно применять для любого количества чисел. Например, для чисел 24, 36 и 48:

48 ÷ 36 = 1 (остаток 12)
36 ÷ 12 = 3 (остаток 0)
24 ÷ 12 = 2 (остаток 0)

Таким образом, НОД(24, 36, 48) = 12.

Метод Эвклида для вычисления нод

Нахождение наибольшего общего делителя двух чисел — это задача, которая решается методом Эвклида. Самый простой способ применить его — использовать деление с остатком.

Для начала находим остаток от деления большего числа на меньшее. Если этот остаток равен нулю, то наименьшее из двух чисел и есть нод. Если остаток не равен нулю, то мы делим меньшее число на остаток и находим новый остаток. Находим остаток от деления наименьшего числа, пока не получим остаток равный нулю. Тот момент, когда мы получили ноль, означает, что последнее меньшее число и есть наибольший общий делитель.

Для примера, пусть нужно найти нод чисел 48 и 18. Сначала находим остаток от деления 48 на 18: 48 mod 18 = 12. Затем, делим 18 на 12 и находим остаток от деления: 18 mod 12 = 6. Далее, делим 12 на 6 и находим остаток: 12 mod 6 = 0. Таким образом, наибольший общий делитель 48 и 18 равен 6.

Метод Эвклида является одним из самых эффективных и простых способов вычисления наибольшего общего делителя двух чисел, и он широко используется в различных областях математики и информатики.

Алгоритм вычисления нод двух чисел

Для вычисления наибольшего общего делителя (нод) двух чисел можно использовать алгоритм Евклида. Он основывается на том, что если находим остаток от деления первого числа на второе, то этот остаток точно не меньше нод этих двух чисел.

1. Найдем остаток от деления большего числа на меньшее: a % b = r. Если r равен 0, то b является искомым нод. Если же r не равен 0, то перейдем к следующему шагу.

2. Повторим прошлый шаг, но теперь числом a будет являться более маленькое число, а числом b — остаток от деления a на b. Если r снова равен 0, то b — наибольший общий делитель. Если же r не равьн 0, то продолжим алгоритм.

3. Повторяем шаг 2 до тех пор, пока не найдем нод.

Пример: Найдем наибольший общий делитель для чисел 28 и 14.

28 % 14 = 0, значит, нод равен 14.

Алгоритм Евклида очень прост и быстро находит наибольший общий делитель, что делает его очень популярным для вычислений в компьютерных программах.

Алгоритм вычисления нод трех чисел

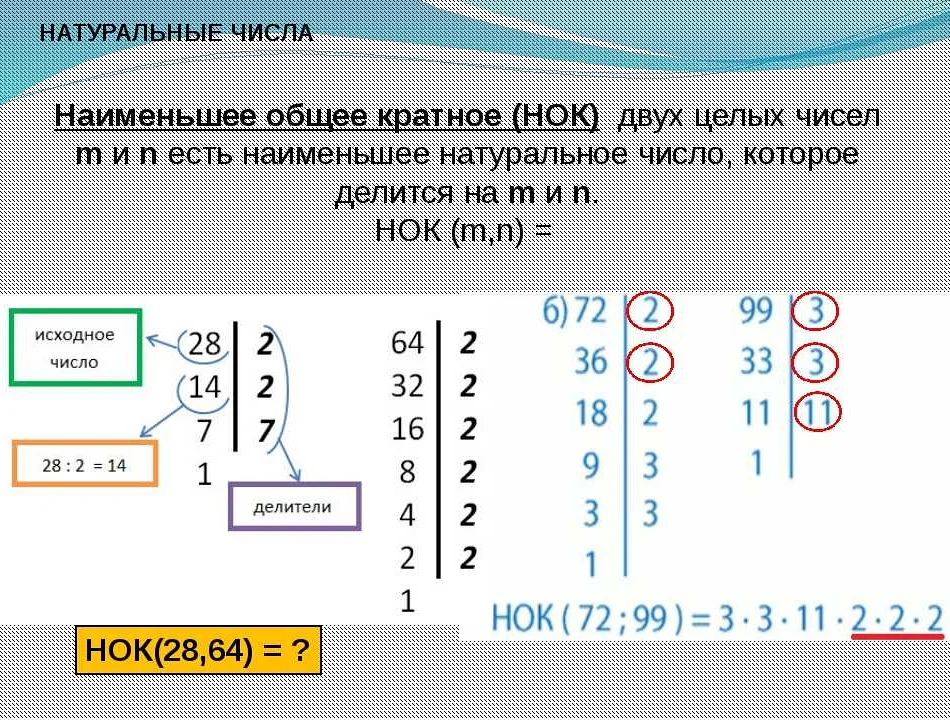
НОД (Наибольший Общий Делитель) – это самое большое число, на которое делятся три заданных числа без остатка.

Алгоритм нахождения НОД трех чисел сводится к последовательному нахождению НОД двух чисел по формуле:

НОД(a, b, c) = НОД(НОД(a, b), c)

Применяем эту формулу некоторое количество раз до тех пор, пока не останется последнее НОД двух чисел:

НОД(a, b) = НОД(b, a % b)

где % обозначает операцию нахождения остатка от деления.

Пример:

Исходные числа:	15	27	81
НОД(15, 27) =	3	НОД(3, 81) =	3

Ответ: НОД(15, 27, 81) = 3.

Свойства нод

Состояние — каждая нода может быть в одном из двух состояний: «открыта» или «закрыта». Это означает, что у нода может быть потомки (если она открыта), или нет (если она закрыта).
Уровень вложенности — это свойство показывает, на каком уровне вложенности находится данная нода. То есть, сколько раз данная нода была вложена в другую ноду.
Количество потомков — это свойство показывает, сколько потомков содержит данная нода. То есть, сколько дочерних нод располагается относительно данной.
Тип элемента — это свойство показывает, является ли данная нода элементом HTML-кода или текстовым узлом. Текстовый узел не имеет дочерних элементов, он содержит только текст.

Пример:

НодаСостояниеУровень вложенностиКоличество потомковТип элемента

html	Открыта	1	1	Элемент HTML-кода
head	Открыта	2	3	Элемент HTML-кода
title	Открыта	3	0	Элемент HTML-кода
text	Закрыта	3	0	Текстовый узел
body	Открыта	2	2	Элемент HTML-кода
div	Открыта	3	1	Элемент HTML-кода
p	Открыта	4	0	Элемент HTML-кода
text	Закрыта	4	0	Текстовый узел
div	Закрыта	3	0	Элемент HTML-кода
p	Закрыта	2	0	Элемент HTML-кода

В данном примере мы имеем HTML-код, состоящий из двух основных элементов — html и body. Внутри элемента html находится head и body. Head в свою очередь содержит элементы title и text. Также внутри body содержится элемент div, который в свою очередь содержит элемент p и текстовый узел.

Применение нод в решении задач

НОД (наибольший общий делитель) является очень полезной математической концепцией, которая используется во многих задачах. Например, когда необходимо разделить несколько предметов на равные группы или найти наименьшее общее кратное двух чисел, мы можем использовать НОД.

В решении задач на число друзей, которые могут разделить ряд предметов между собой, мы можем использовать НОД. Если количество предметов не делится на количество друзей без остатка, то возникает вопрос о том, сколько предметов должен получить каждый друг, чтобы они были одинакового размера. В этом случае НОД помогает найти максимальное количество предметов, которые можно разделить равномерно между всеми друзьями.

Также, НОД используется в задачах на наименьшее общее кратное. Например, если мы хотим найти наименьшее общее кратное (НОК) двух чисел, мы можем использовать формулу НОК = (число 1 * число 2) / НОД. Это формула работает потому, что НОК всегда является произведением двух чисел, разделенных на их НОД.

Таким образом, понимание того, как использовать НОД, может помочь в решении многих математических задач, связанных с разделением и сокращением.

Решение задач на вычисление нод

Задача 1. Найти наибольший общий делитель чисел 24 и 30.

Решение:

Найдем все делители числа 24: 1, 2, 3, 4, 6, 8, 12, 24.
Найдем все делители числа 30: 1, 2, 3, 5, 6, 10, 15, 30.
Общие делители: 1, 2, 3, 6.
Наибольший общий делитель — наибольший из общих делителей, т.е. НОД(24, 30) = 6.

Задача 2. Найти наибольший общий делитель чисел 42 и 28.

Решение:

Найдем все делители числа 42: 1, 2, 3, 6, 7, 14, 21, 42.
Найдем все делители числа 28: 1, 2, 4, 7, 14, 28.
Общие делители: 1, 2, 7, 14.
Наибольший общий делитель — наибольший из общих делителей, т.е. НОД(42, 28) = 14.

Практическое применение нод в жизни

НОД (наибольший общий делитель) – это одно из базовых понятий в математике, которое находит свое практическое применение в различных областях жизни. Особенно часто НОД используется в экономике и финансах, при решении различных задач, связанных с оптимизацией и распределением ресурсов.

Например, если у компании есть несколько заказов с различными сроками исполнения, то НОД поможет определить минимальный общий срок, за который все заказы могут быть выполнены. Аналогично, при расчете налогов, НОД может быть использован для определения общей стоимости имущества, на основе которой будет происходить налогообложение.

НОД также широко используется в технике и науке. Например, в электронике его часто применяют для определения оптимального соотношения частоты и шага микропроцессорного сигнала, чтобы достичь максимальной производительности устройства.

В целом, НОД – это неотъемлемая часть математики, которая находит свое применение в различных сферах жизни, помогая решать сложные задачи и оптимизировать процессы.

Резюме

В процессе изучения математики в 5 классе ученики сталкиваются с понятием «нода». Нода — это узел на графике, который является точкой пересечения двух или более стержней на диаграмме.

Ноды используются для решения задач, связанных с графиками и диаграммами. Они помогают определить точку, где два объекта пересекаются или взаимодействуют друг с другом, что может быть полезно в контексте физики, химии, экономики и других дисциплин.

Учителя математики в 5 классе на протяжении всего года обучения учеников уделяют особое внимание пониманию и использованию нод. Они помогают ученикам развивать навыки анализа и решения проблем, что может быть полезно не только в математике, но и в жизни в целом.

В целом, понимание ноды и ее использование — это важный аспект в изучении математики в 5 классе, который позволяет ученикам развивать навыки решения задач и аналитического мышления, что будет полезно во многих других областях их жизни.

Вопрос-ответ:

Что такое нод в математике 5 класс определение?

НОД (Наибольший общий делитель) двух чисел – это наибольшее число, которое делит оба этих числа без остатка. Например, НОД чисел 20 и 30 равен 10, т.к. 10 делит и 20, и 30 без остатка, а больше чем 10 получить не удастся.

Какие свойства имеет НОД?

НОД обладает несколькими свойствами: 1) Если a и b — неотрицательные целые числа и a делится на b без остатка, то НОД(a,b) = b. 2) Если c делит и a, и b, то c также делит и НОД(a,b). 3) Для любых целых чисел a,b и c выполняется тождество НОД(a,b) = НОД(a, b+ac).

Как находить НОД?

Существует несколько способов нахождения НОД: 1) Разложить каждое число на простые множители и найти общие множители. НОД будет равен произведению этих множителей. 2) Использовать алгоритм Евклида. Его суть заключается в последовательном вычитании из большего числа меньшего до тех пор, пока не получится два равных числа. НОД будет равен этому числу. Например, для чисел 84 и 30: 84-30=54, 30-54=-24 (вычитание изменить знак). Отбросим отрицательность и продолжим: 54-(-24)=78, 24-78=-54, 54-(-54)=108, 54-108=-54, 0-(-54)=54. Получаем, что НОД(84,30)=54.

Зачем нужен НОД в математике 5 класс?

НОД используется во многих областях математики, в том числе в алгебре и геометрии. В 5 классе его часто рассматривают в рамках изучения делимости чисел и разложения на простые множители, что является основой арифметических операций с целыми числами.

Как находить НОД большого множества чисел?

Для этого можно использовать алгоритм Евклида для двух чисел, примененный к каждой паре чисел из множества, затем снова к каждой паре и т.д. до тех пор, пока не получится одно число. Например, для нахождения НОД чисел 12, 18 и 30: НОД(12,18)=6, НОД(6,30)=6.