Нумерация в математике — это система символов или цифр, используемых для обозначения чисел в порядке их возрастания или убывания. В статье рассматриваются различные системы нумерации, применяемые в математике, и их особенности.
Нумерация – это система, которая используется для обозначения чисел. Она является одной из основных и фундаментальных концепций математики и представляет собой процесс, посредством которого числа превращаются в удобочитаемый и понятный формат.
Нумерация играет огромную роль в повседневной жизни человека – мы используем ее для того, чтобы установить порядок, отличить одно количество от другого и решать различные задачи, связанные с математическими операциями. Для этого нам нужно знать особенности каждой системы нумерации и уметь переводить числа из одной системы в другую.
В настоящее время наиболее распространены две системы нумерации – десятичная и двоичная. Десятичная система нумерации основана на десяти цифрах, от 0 до 9, и используется повсеместно в повседневной жизни. Двоичная система нумерации, с другой стороны, основана на двух цифрах, 0 и 1, и широко применяется в компьютерных технологиях и электронике.
Определение и принципы нумерации

Нумерация – это процесс отображения чего-либо в численной форме. В математике нумерация используется для идентификации и упорядочивания объектов и чисел. Зачастую нумерация обеспечивает удобство и точность в работе с числами и данными.
В математике упорядочивание элементов по номерам происходит с помощью последовательности чисел, следующих друг за другом в порядке возрастания или убывания. Принципы нумерации включают в себя нумерацию целых чисел, рациональных чисел, иррациональных чисел и комплексных чисел.
Нумерация целых чисел начинается с нуля и, соответственно, содержит отрицательные и положительные целые числа. Рациональные числа нумеруются с помощью дробей, которые содержат целое числитель и знаменатель (ненулевой целый делитель) – каждая дробь соответствует определенному числу. Иррациональные числа не могут быть записаны в виде дроби и имеют бесконечную десятичную дробь с нерегулярным повторением цифр. Наконец, комплексные числа нумеруются на плоскости с помощью действительной и мнимой оси.
- Нумерация – это процесс отображения объектов и чисел в численной форме
- Нумерация используется для идентификации и упорядочивания элементов
- Принципы нумерации включают в себя нумерацию целых, рациональных, иррациональных и комплексных чисел
- Целые числа начинаются с нуля, рациональные – с помощью дробей, иррациональные – не могут быть записаны в виде дроби, а комплексные нумеруются на плоскости с помощью действительной и мнимой оси
Какие системы нумерации существуют

Существует много систем нумерации, но наиболее распространены в повседневной жизни следующие:
- Десятичная система – основана на использовании 10 цифр: 0,1,2,3,4,5,6,7,8,9. Она используется повсеместно, включая финансовые операции, математику и компьютерные программы.
- Двоичная система – основывается на использовании всего 2 цифр: 0 и 1. Она используется в электронике и компьютерной технике, где два состояния выключено и включено могут быть представлены двумя значениями.
- Восьмеричная система – основывается на использовании 8 цифр: 0,1,2,3,4,5,6,7. Она также используется в электронике и компьютерной технике, но менее распространена, так как двоичная система предпочтительнее.
- Шестнадцатеричная система – основывается на использовании 16 цифр: 0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F. Она часто используется в программировании и компьютерной технике для представления цветов и адресов памяти.
Кроме этих систем нумерации, существуют и другие, такие как троичная и двадцатиричная, но они менее распространены и используются только в специфических областях.
Система десятичной нумерации
Десятичная нумерация является одной из наиболее распространенных систем нумерации в нашей жизни. Она основана на использовании десяти цифр: от 0 до 9. Каждая цифра является разрядом, а ее значение определяется ее позицией в числе.
Например, число 456 может быть записано как 4*10^2 + 5*10^1 + 6*10^0, где ^ обозначает степень. Таким образом, цифра “4” находится в разряде “сотен”, цифра “5” в разряде “десятков”, а цифра “6” в разряде “единиц”.
Десятичная нумерация используется во многих сферах, где требуется работать с числами, таких как финансы, наука, техника и т.д. Кроме того, она является основой для других систем нумерации, таких как двоичная и шестнадцатеричная.
При работе с десятичной нумерацией важно уметь складывать, вычитать, умножать и делить числа. Также стоит понимать, как конвертировать числа из одной системы нумерации в другую.
В целом, система десятичной нумерации является неотъемлемой частью нашей культуры и пространства, в котором мы живем, что делает ее важной для изучения и понимания.
Система двоичной нумерации
В математике есть различные системы нумерации, и одной из них является двоичная система нумерации. Как следует из названия, эта система использует всего две цифры: 0 и 1. Используя только две цифры, можно представить любое число в двоичном формате.
Для того чтобы записать число в двоичной системе, вам нужно разбить его на степени двойки. Затем необходимо записать коэффициенты для каждой степени двойки, начиная со степени, равной самому высокому числу.
Например, если вы хотите записать число 13 в двоичной системе, вам нужно разбить его на степени двоек: 8, 4, 2 и 1. Далее замените каждую степень двойки на соответствующую цифру в двоичной системе. Если степень присутствует в числе, то коэффициент равен 1, в противном случае — 0.
Таким образом, число 13 в двоичной системе будет записано как 1101. Первая цифра соответствует двойке в степени 3 (8), которая присутствует в исходном числе. Далее идет двойка в степени 2 (4), которая также есть в исходном числе. Далее — двойка в степени 1 (2), которой нет в числе, поэтому коэффициент равен 0. И, наконец, последняя цифра соответствует единице в степени 0 (1), которая присутствует в исходном числе.
Система восьмеричной нумерации
Восьмеричная система нумерации – это система с основанием 8. В этой системе используются цифры от 0 до 7. Как и в двоичной и шестнадцатеричной системах, восьмеричная система часто используется в компьютерных науках.
Для обозначения чисел в восьмеричной системе используется префикс “0” и “o”, например, число 25 в восьмеричной системе написано как “031”.
Как и в любой другой системе с основанием отличным от 10, числа в восьмеричной системе приравниваются к степеням основания (8) в соответствии с их позицией в числе, начиная справа налево.
Например, число “031” в восьмеричной системе можно перевести в десятичную систему следующим образом: 1 * 8^1 + 3 * 8^0 = 8 + 3 = 11.
Восьмеричная система нумерации также может быть использована для представления двоичных данных, например, восьмеричное число “311” соответствует двоичному числу “11001101”.
Система шестнадцатеричной нумерации
Шестнадцатеричная система нумерации – это система счисления, основанная на 16 символах: цифры от 0 до 9 и латинские буквы от A до F (или a до f).
В шестнадцатеричной системе каждая цифра представляет собой определенное количество единиц, умноженное на 16 в степени, соответствующей позиции числа. Например, число 3AC в шестнадцатеричной системе представляет собой:
- 3 x 16^2 (или 768)
- A x 16^1 (или 160)
- C x 16^0 (или 12)
Итого: 3AC = 768 + 160 + 12 = 940 (в десятичной системе).
Шестнадцатеричная система широко используется в информатике, особенно для представления цветов и адресов памяти. Каждый цвет можно представить как комбинацию трех шестнадцатеричных чисел, обозначающих уровень красного, зеленого и синего. Например, цвет #FF0000 представляет максимально возможный уровень красного и минимальный уровень зеленого и синего.
Шестнадцатеричная цифраДесятичное значение
| 0 | 0 |
| 1 | 1 |
| 2 | 2 |
| 3 | 3 |
| 4 | 4 |
| 5 | 5 |
| 6 | 6 |
| 7 | 7 |
| 8 | 8 |
| 9 | 9 |
| A (или a) | 10 |
| B (или b) | 11 |
| C (или c) | 12 |
| D (или d) | 13 |
| E (или e) | 14 |
| F (или f) | 15 |
Учитывая разницу в количестве символов в разных системах счисления, можно заметить, что шестнадцатеричная система намного компактнее и удобнее для использования в некоторых случаях, например, при работе с цветом и памятью.
Перевод чисел из одной системы нумерации в другую
Система счисления – это способ записи чисел при помощи цифр и их соответствующих разрядов. В математике самые распространенные системы счисления это десятичная (основа 10), бинарная (основа 2) и шестнадцатеричная (основа 16).
Конвертирование числа из одной системы счисления в другую может оказаться полезным, особенно если имеется дело с компьютерными приложениями и программированием. Для перевода числа из одной системы нумерации в другую следует использовать базу целевой системы и правила перевода из системы исходного числа.
Например, чтобы перевести число 267 из десятичной системы счисления в двоичную, нужно последовательно разделить число на 2 и оставлять остатки до тех пор, пока результат деления не станет равен 0. В этом примере результатом будет 100001011, что означает, что 267 в десятичной системе равно 100001011 в двоичной системе.
Для перевода числа из двоичной системы счисления в десятичную, нужно просуммировать произведения каждой цифры числа на 2 в степени, которая соответствует позиции цифры в числе, начиная с нулевой степени. Например, число 1101010 в двоичной системе счисления переводится в десятичную следующим образом:
| 7 | 6 | 5 | 4 | 3 | 2 | 1 |
| 1 | 1 | 0 | 1 | 0 | 1 | 0 |
В итоге получается: 1*2^6 + 1*2^5 + 0*2^4 + 1*2^3 + 0*2^2 + 1*2^1 + 0*2^0 = 90. Таким образом, число 1101010 в двоичной системе счисления эквивалентно числу 90 в десятичной системе счисления.
Значение позиций чисел в разрядной системе нумерации
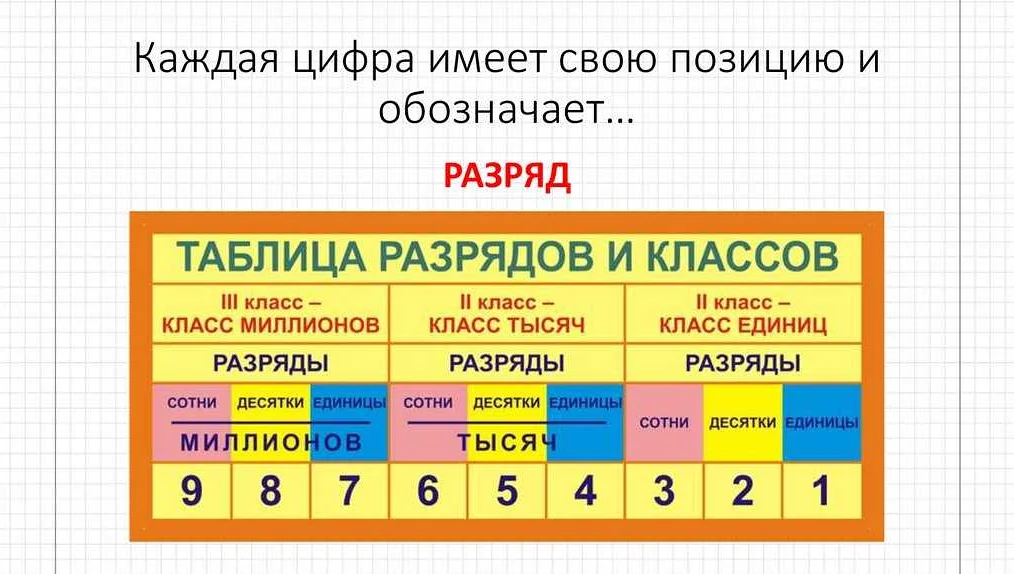
Разрядная система нумерации, также известная как позиционная система, основана на том, что значение числа зависит от позиции числа в числовой последовательности. В этой системе числа записываются с помощью цифр и различных степеней числа, которые указывают на позицию цифры в числе.
При записи числа каждая цифра занимает конкретную позицию в числе, которая определяет ее значение. Например, в числе 247, 2 находится в позиции сотен, 4 в позиции десятков и 7 в позиции единиц. Значение каждой цифры зависит от позиции, которую она занимает в числе.
Для примера, рассмотрим число 357. Каждая цифра в этом числе имеет свое значение, которое зависит от ее позиции. 3 находится в позиции сотен, значит, его значение равно 300. 5 находится в позиции десятков, значит, его значение равно 50. И, наконец, 7 находится в позиции единиц, значит, его значение равно 7. Таким образом, значение числа 357 равно сумме значений каждой цифры в его позиции: 300 + 50 + 7 = 357.
Разрядная система нумерации является основой для всех систем нумерации, используемых в математике и науке. Она также позволяет использовать более компактную запись чисел, поскольку более большие числа могут быть записаны с помощью меньшего количества цифр.
Применение нумерации в информатике и компьютерах
Нумерация является важной составляющей в информатике и компьютерах. Она используется при многих операциях, таких как индексирование, сортировка и фильтрация данных.
Одним из примеров применения нумерации является нумерация строк и столбцов в таблицах. Она позволяет легко ориентироваться в большом объеме данных и быстро находить нужную информацию.
Нумерация также используется в адресации веб-страниц и электронных документов. Она помогает быстро переходить на нужную страницу и легко находить необходимую информацию.
В программировании нумерация используется для обращения к элементам массивов, элементам списка, символам строк и многим другим объектам. Это позволяет удобно обрабатывать и анализировать данные в процессе написания кода.
Итак, использование нумерации в информатике и компьютерах является неотъемлемой частью многих операций и позволяет упростить обработку больших объемов данных, а также повысить эффективность работы с ними.
Вопрос-ответ:
Каково значение нумерации в математике?
Нумерация в математике предназначена для упорядочивания и идентификации элементов множества. Она позволяет присвоить каждому элементу числовое значение и определить его место в порядке следования.
Какие виды нумерации используются в математике?
В математике используются различные виды нумерации, такие как естественная, целочисленная, дробная, десятичная, римская, двоичная, восьмеричная, шестнадцатеричная и др.
Что означает естественная нумерация?
Естественная нумерация – это нумерация натуральных чисел, начиная с единицы: 1, 2, 3, 4, 5 и т.д.
Как применяется нумерация в алгебре?
В алгебре нумерация используется для идентификации переменных и коэффициентов. Например, в выражении 2x + 5y = 10 переменная x имеет номер 1, переменная y – номер 2, а коэффициенты 2, 5 и 10 – это элементы множества с порядковыми номерами 1, 2 и 3 соответственно.
Как применяется нумерация в теории вероятностей?
В теории вероятностей нумерация используется для задания вероятностей событий. Например, если имеется множество А = {a, b, c, d, e, f} и каждому элементу этого множества соответствует вероятность 1/6, то вероятность события “выпадение числа 4” равна 1/6.
Какие математические объекты можно пронумеровать?
В математике могут быть пронумерованы различные объекты, такие как числа, множества, точки, линии, плоскости, пространства и т.д.
Какова роль нумерации в геометрии?
В геометрии нумерация используется для идентификации точек, линий и других геометрических объектов. Она позволяет задавать координаты точек, определять расстояние между точками и строить графики функций.
Примеры задач на нумерацию в школьной математике
Задание 1. На стене висит 10 картин. Найдите порядковый номер четвертой по счету картинки.
Решение: Порядковый номер четвертой картинки равен 4.
Задание 2. В книжном магазине продается 20 книг. Они пронумерованы от 1 до 20. Каков номер книги, если ее номер больше на 7, чем номер предыдущей?
Решение: Пусть номер искомой книги равен Х. Тогда предыдущая книга имеет номер Х-1. Согласно условию задачи, Х – (Х-1) = 7. Решив уравнение, получим, что номер искомой книги равен 8.
Задание 3. В группе 25 учеников. Их ФИО занесены в таблицу, которая содержит 5 столбцов. Каков порядковый номер ученика, стоящего во втором столбце, если в этом столбце находятся ученики с 6-го по 10-й?
1 столбец2 столбец3 столбец4 столбец5 столбец
| 1-й ученик | 6-й ученик | 11-й ученик | 16-й ученик | 21-й ученик |
| 2-й ученик | 7-й ученик | 12-й ученик | 17-й ученик | 22-й ученик |
| 3-й ученик | 8-й ученик | 13-й ученик | 18-й ученик | 23-й ученик |
| 4-й ученик | 9-й ученик | 14-й ученик | 19-й ученик | 24-й ученик |
| 5-й ученик | 10-й ученик | 15-й ученик | 20-й ученик | 25-й ученик |
Решение: Ученик, стоящий во втором столбце и имеющий порядковый номер 6, стоит на месте (1-1)*5+2 = 2. То есть он занимает второе место в первой строке таблицы. Для того, чтобы найти порядковый номер ученика, стоящего во втором столбце на месте 6, надо прибавить 5 к порядковому номеру предыдущего ученика (на месте 2), получим 10. То есть ученик, стоящий на месте 6 во втором столбце, имеет порядковый номер 10.






