Объемный прямоугольник в математике называется параллелепипедом. Узнайте об особенностях этой геометрической фигуры и как вычислить её объем.
В математике есть несколько терминов, обозначающих объемные фигуры. Одной из таких фигур является прямоугольник, который обладает не только площадью, но и объемом. Объемный прямоугольник, как следует из его названия, представляет собой прямоугольную фигуру в трехмерном пространстве.
Объемный прямоугольник имеет шесть граней, которые являются прямоугольниками. Длина каждой из сторон может быть разной, но важно помнить, что объем прямоугольника вычисляется по формуле V = a * b * c, где a, b и c — это длины трех сторон прямоугольника.
Объемный прямоугольник используется в различных областях математики, физики и инженерии. Например, при расчете объема жидкостей, газов или при проектировании строительных конструкций. Изучение объемных фигур помогает исследовать основные законы трехмерной геометрии и приложить их на практике.
Определение понятия
Объемный прямоугольник (или просто параллелепипед) — это трехмерная геометрическая фигура, имеющая три пары параллельных граней, каждая из которых является прямоугольником. Объемный прямоугольник имеет шесть прямоугольных граней, 12 ребер и восемь вершин.
Для нахождения объема прямоугольника необходимо перемножить длину, ширину и высоту. Формула для нахождения объема выглядит следующим образом:
| Формула: | Объем = длина * ширина * высота |
Объемный прямоугольник находит широкое применение в геометрии, архитектуре, строительстве, инженерии и других науках, которые связаны с изучением трехмерных форм и их применением в реальном мире.
Также стоит отметить, что объекты, которые можно приблизить объемными прямоугольниками, называются блоками.
Формула расчета объема
Объем прямоугольного параллелепипеда — это объем пространства, занимаемого фигурой в форме прямоугольника. Формула расчета объема прямоугольника достаточно проста и строится на основе трех соответствующих измерений: длины, ширины и высоты.
Формула: V = a * b * c
- V — объем прямоугольного параллелепипеда
- a — длина
- b — ширина
- c — высота
Таким образом, чтобы определить объем прямоугольного параллелепипеда, нужно умножить длину, ширину и высоту, которые выражаются в одинаковых единицах измерения.
Данную формулу можно удобно применять на практике, особенно при расчете объема контейнеров, ящиков, коробок и других подобных объектов.
Виды объемных прямоугольников
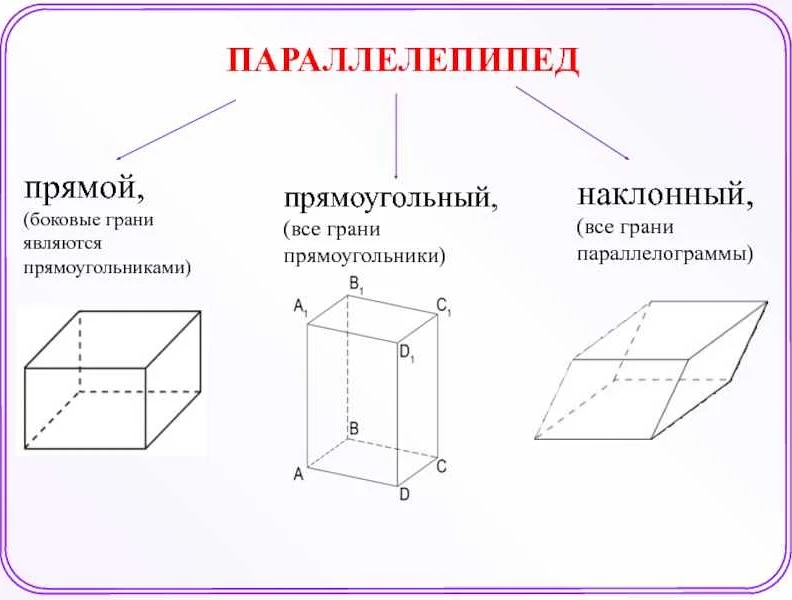
Объемный прямоугольник, известный также как параллелепипед, является фигурой, состоящей из шести прямоугольных граней. Прямоугольник может иметь различную форму, размеры и соотношение сторон. На основании этих характеристик можно выделить несколько видов объемных прямоугольников, которые часто используются в математике и инженерных расчетах.
- Куб — это объемный прямоугольник, у которого все стороны равны между собой.
- Квадратный параллелепипед — это прямоугольный параллелепипед, у которого две пары смежных сторон равны между собой.
- Прямоугольный параллелепипед — это прямоугольный объемный прямоугольник любых размеров и пропорций.
Одним из важных понятий, связанных с объемными прямоугольниками, является их объем. Объемный прямоугольник можно выразить через длину, ширину и высоту, используя формулу: объем = длина x ширина x высота. Также можно использовать площадь одной из граней и высоту, чтобы найти объем: объем = площадь грани x высота.
Характеристики объемного прямоугольника
Объемный прямоугольник — это геометрический объект, который обладает несколькими характеристиками:
- Длина: это длина прямоугольника вдоль его наибольшей стороны.
- Ширина: это ширина прямоугольника вдоль его менее длинной стороны.
- Высота: это высота прямоугольника, которая измеряется вдоль его третьей стороны.
- Диагонали: это линии, которые соединяют противоположные вершины прямоугольника.
- Боковые грани: это стороны прямоугольника, которые находятся на одном уровне высоты и соединяют соответствующие вершины.
- Площадь поверхности: это сумма площадей всех граней прямоугольника.
- Объем: это пространство, которое занимает объемный прямоугольник.
Эти характеристики очень важны, когда нужно определить размеры прямоугольной упаковки для товара, объем аквариума или грузового отсека транспортного средства. Знание этих характеристик поможет правильно рассчитать объем, площадь поверхности или количество материала, необходимого для изготовления нужного размера прямоугольника.
Построение объемных прямоугольников в пространстве
Объемный прямоугольник может быть построен в пространстве с помощью трех измерений: длины, ширины и высоты. Для построения прямоугольника необходимо иметь три стороны, соответствующие каждому измерению. Длина и ширина определяются в плоскости, а высота — перпендикулярна к этой плоскости.
Объем прямоугольника вычисляется путем умножения длины, ширины и высоты:
Объем = длина x ширина x высота
При построении объемного прямоугольника важно учитывать правила геометрии. Например, параллельные грани должны иметь одинаковую ширину и длину, а стороны должны быть перпендикулярны между собой.
Объемные прямоугольники широко используются в инженерии и архитектуре для проектирования зданий и конструкций. Использование объемных прямоугольников позволяет точно определить объемы расходуемых материалов и убедиться в корректности размещения объектов в пространстве.
Построение объемных прямоугольников также может быть использовано для моделирования твердых тел в физике и математике. Множество вычислительных задач, разработка программ и расчетов при этом сводится к работе с объемными прямоугольниками.
Задачи на нахождение объема
Одной из главных задач математики является нахождение объема геометрических фигур. Объем — это мера, которая показывает, сколько места занимает тело в пространстве. Важно помнить, что каждая фигура имеет свой собственный способ нахождения объема. В этой статье мы рассмотрим некоторые из задач на нахождение объема.
Задача 1. Найти объем куба
Куб — это прямоугольный параллелепипед, все его грани равны друг другу. Объем куба можно вычислить, умножив длину его ребра на само себя три раза: V = a³.
Задача 2. Найти объем цилиндра
Цилиндр — это тело, образованное двумя круглыми основаниями и цилиндрической оболочкой. Объем цилиндра можно найти, умножив площадь основания (πr²) на высоту (h): V = πr²h.
Задача 3. Найти объем пирамиды
Пирамида — это тело, образованное многогранной основой и треугольными гранями, сходящимися в вершину. Объем пирамиды можно найти по формуле V = 1/3Sh, где S — площадь основания, h — высота пирамиды.
Задача 4. Найти объем шара
Шар — это тело, все точки которого находятся на одинаковом расстоянии от центра. Объем шара можно найти, используя формулу V = 4/3πr³, где r — радиус шара.
Все вышеописанные формулы позволяют находить объемы различных тел. Они могут быть использованы для решения задач в различных областях науки и техники. Но помните — формулы нужно применять правильно, с учетом условий задачи и с учетом единиц измерения!
Некоторые свойства объемных прямоугольников

Объемный прямоугольник — это геометрическое тело, ограниченное шестью прямоугольниками. В математике он часто используется для вычисления объема различных объектов.
Одно из основных свойств объемных прямоугольников — их объем можно вычислить по формуле: V = a * b * c, где a, b и c — длины трех сторон прямоугольника.
Также объемный прямоугольник имеет три пары параллельных граней. Это означает, что любую из сторон можно рассматривать как основание прямоугольника, а две другие стороны будут выступать в роли боковых граней.
Кроме того, объемные прямоугольники могут быть различными по пропорциям сторон. Если все три стороны одной длины, получится куб. Такие же по пропорциям могут быть и боковые грани. Например, при равных соотношениях между длиной, шириной и высотой, получится правильный прямоугольный параллелепипед.
- Объемный прямоугольник можно разрезать поперек. В результате получится несколько параллелепипедов, объемы которых можно вычислить отдельно и сложить.
- Объемный прямоугольник может быть представлен как обобщенная ориентированная площадь. Такое представление данного геометрического тела может использоваться для решения различных задач в математике и физике.
Несмотря на свою простоту, объемные прямоугольники являются важным инструментом для решения математических задач. Их свойства и формулы позволяют проводить вычисления в разномасштабных задачах, начиная от вычисления объема бассейна до расчетов объемов сложных многогранных тел.
Объемный прямоугольник в геометрии
Объемный прямоугольник — это геометрическое тело, которое имеет форму прямоугольного параллелепипеда. Он состоит из шести прямоугольных граней, каждая из которых имеет две параллельные стороны и прямой угол между ними. Объемный прямоугольник характеризуется тремя линейными размерами — длиной, шириной и высотой.
Для вычисления объема прямоугольника в геометрии используется формула V = a * b * c, где a, b и c — это длина, ширина и высота соответственно. Объем измеряется в кубических единицах, таких как кубический метр или кубический дециметр.
Объемный прямоугольник широко используется в различных областях математики и науки, таких как геометрия, физика, инженерия и строительство. Он часто применяется для определения объема геометрических тел и расчета объемов жидкостей и газов в контейнерах и резервуарах.
- Характеристики объемного прямоугольника в геометрии:
- Имеет форму прямоугольного параллелепипеда.
- Состоит из шести прямоугольных граней.
- Характеризуется тремя линейными размерами — длиной, шириной и высотой.
Объемный прямоугольник является одним из наиболее простых геометрических тел, поэтому он широко используется при решении математических задач и в реальных приложениях. Его легко понять и рассчитать объем, что делает его незаменимым инструментом при работе с объемными данными и расчетами.
Применение в различных отраслях науки и техники
Строительство: объемные прямоугольники используются в строительстве для определения объемов фундаментов, стен и потолков. Они также помогают инженерам и архитекторам в расчетах строительных материалов, таких как бетон, кирпичи и дерево. Объемные прямоугольники используются для определения экономической эффективности проектов застройки территории.
Производство: объемные прямоугольники используются в промышленности для контроля объемов производства и хранения продуктов. Например, производители пищевых продуктов могут использовать объемные прямоугольники для установления оптимального размера упаковки товара.
Наука: объемные прямоугольники используются в многих научных исследованиях. В физике, объемный прямоугольник может помочь в расчетах гидродинамики и определении объемов пространства. В химии, объемные прямоугольники могут использоваться для измерения объема жидкостей и газов.
Транспорт: объемные прямоугольники используются в транспортной индустрии для определения объема грузовых отсеков и багажных отсеков самолетов, вагонов и автомобилей. Это помогает оптимизировать производство и обеспечить безопасность пассажиров.
Инженерия: инженеры используют объемные прямоугольники для определения объемов твердых тел, использования в компьютерном моделировании и виртуальной реальности. Объемные прямоугольники помогают представлять объекты в трехмерном пространстве и понимать их свойства.
История возникновения понятия объемного прямоугольника
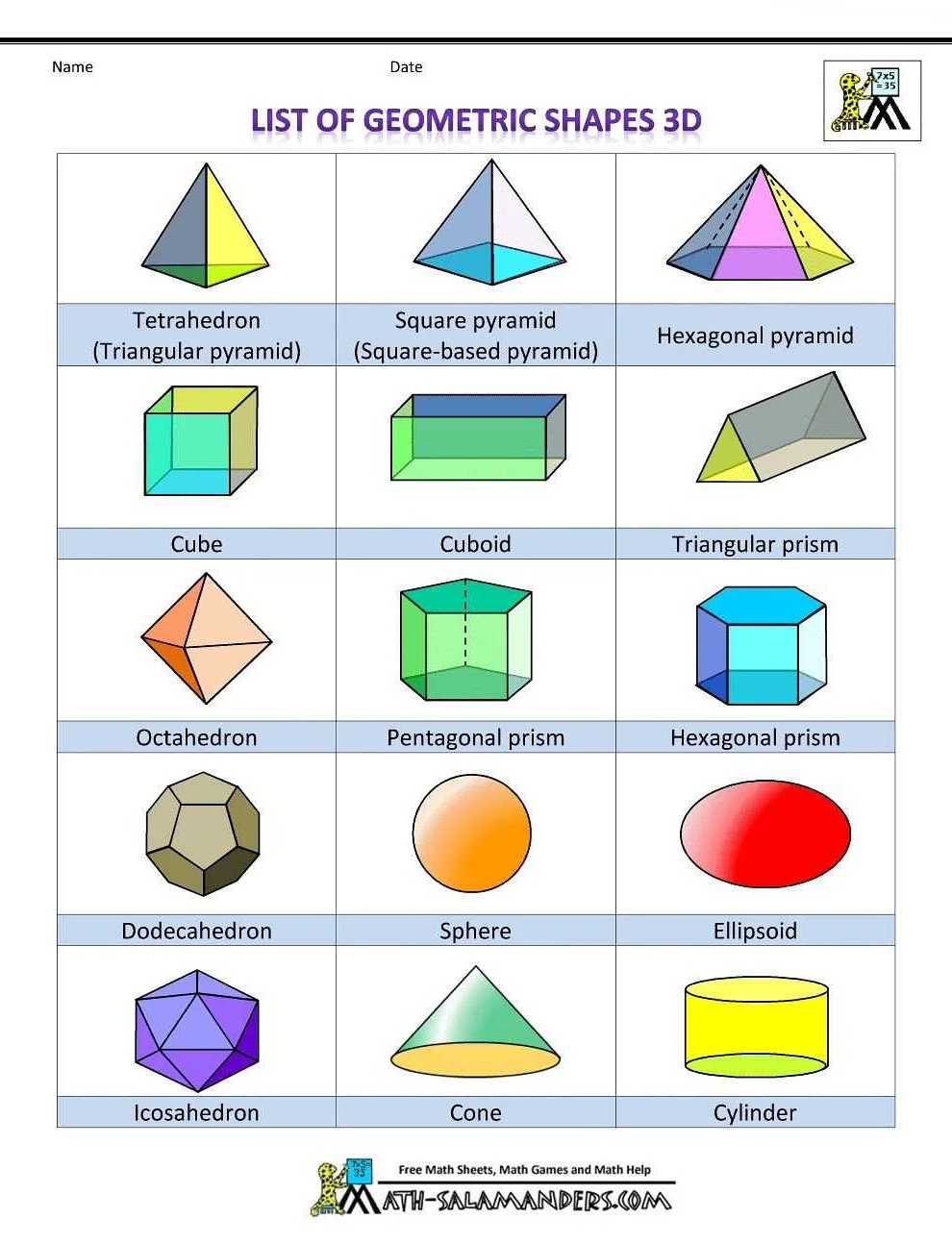
Понятие объема первоначально было связано с измерением объема жидкостей и зерновых культур, ведь это были вещества, которые измеряли в кувшине или мерной ложке. Однако в дальнейшем понятие объема расширилось, и начали измерять объем твердых тел, таких как геометрические фигуры.
Объем прямоугольника начали изучать еще в Древней Греции и Египте. В этих странах математики развивались самостоятельно, поэтому у них были свои методы и подходы. Например, греки использовали метод сечений, а египтяне — метод альтернативного повторения.
Одним из первых, кто впервые определил объем прямоугольника, был Евклид. В своем труде «Начала» он доказал, что объем прямоугольного параллелепипеда равен произведению его длины, ширины и высоты.
В дальнейшем, на основе работ Евклида, математики стали изучать объем более сложных геометрических фигур, таких как тела вращения и пирамиды. С развитием математического аппарата стали появляться новые способы расчета объемов, однако до сих пор формула для расчета объема прямоугольного параллелепипеда является базовой и широко используется.
- Изначально понятие объема начали изучать в связи с измерением объема жидкостей и зерновых культур.
- Первые математики, которые изучали объем прямоугольника, появились в Древней Греции и Египте.
- Евклид одним из первых определил объем прямоугольника в своем труде «Начала».
- С развитием математического аппарата стали появляться новые способы расчета объемов более сложных геометрических фигур.
Вопрос-ответ:
Как называется фигура, которая получается, если поставить на ребро квадрата еще один квадрат?
Такая фигура называется куб.
Что такое прямоугольный параллелепипед?
Прямоугольный параллелепипед — это объемная геометрическая фигура, у которой все грани являются прямоугольниками, а противоположные стороны равны между собой.
Как вычислить объем прямоугольного параллелепипеда?
Объем прямоугольного параллелепипеда можно вычислить по формуле V = a * b * c, где a, b и c — длины трех взаимно перпендикулярных ребер.
Какие свойства имеет прямоугольный параллелепипед?
Прямоугольный параллелепипед имеет такие свойства как: все грани являются прямоугольниками; противоположные грани параллельны и равны по размеру; противоположные ребра равны; каждая диагональ параллелепипеда является осью симметрии.
Какое отношение между объемом прямоугольного параллелепипеда и его боковой поверхностью?
Нет строго определенного отношения между объемом прямоугольного параллелепипеда и его боковой поверхностью, так как величины этих параметров зависят от размеров фигуры. Однако, можно сказать, что боковая поверхность параллелепипеда представляет собой сумму площадей всех боковых граней.
Каковы особенности расчета площади боковой поверхности прямоугольного параллелепипеда?
Для расчета площади боковой поверхности прямоугольного параллелепипеда необходимо умножить периметр основания на высоту. При этом, если все стороны основания равны (квадратный параллелепипед), то площадь боковой поверхности равна удвоенной площади одной из граней.
Каковы примеры использования прямоугольного параллелепипеда в повседневной жизни?
Прямоугольный параллелепипед является очень распространенной фигурой и используется в различных сферах жизни: в строительстве (кирпич, блоки, бетонные плиты), в упаковке товаров (коробки, контейнеры), в производстве мебели (шкафы, комоды), в обучении (геометрические модели), и т.д.






