Развертка – это процесс превращения трехмерной фигуры в плоскость. В математике она применяется для удобства расчетов и построений. Узнайте больше о том, что такое развертка и как ее делать.
Развертка – одно из понятий геометрии, которое используется для описания тел, окружностей и других математических фигур. Этот термин подразумевает раскрытие поверхности объекта на плоскость, в виде развертки. Она представляет собой плоскую фигуру, которую можно получить путем разрезания и расправления поверхности тела.
Когда развертывают поверхность, они делают это, чтобы легче рассчитать его площадь или общий объем. Эта техника также может быть использована для создания дизайна объектов, из которых потом будут сделаны эскизы для их производства.
В этой статье мы рассмотрим основные принципы развертки, примеры ее использования в геометрии и инженерии, а также узнаем, какие задачи решает математик в процессе работы с разверткой.
Развертка в математике: основная информация

Развертка в математике – это процесс преобразования трехмерной фигуры в двумерную плоскую сетку. Это полезный инструмент для работы с геометрическими объектами и их изображениями.
Процесс развертки включает в себя разбиение поверхности фигуры на части и растягивание этих частей до плоской формы, что позволяет легко изучать параметры и свойства фигуры. Развертки широко используются в областях, где трехмерные объекты требуются представлять и обрабатывать на двумерном уровне, таких как промышленный дизайн, архитектура и теория игр.
Типичным примером развертки является процесс создания шаблона для складывания бумажной фигуры, такой как коробка. С помощью развертки, можно создать бумажный шаблон, который легко складывается в трехмерную форму. Этот метод широко используется в моделировании и играх, где развертка позволяет создавать сложные фигуры, которые затем можно преобразовывать в игровую символику или анимированные персонажи.
Существует множество методов развертки в математике, включая методы преобразования, методы минимизации и методы ограничения. Каждый метод имеет свои преимущества и недостатки, и выбор метода зависит от конкретной задачи и типа фигуры.
- Преобразование: Этот метод основан на преобразовании трехмерной фигуры в цилиндр, который затем можно разрезать и распространить на плоскости.
- Минимизация: Этот метод использует алгоритмы минимизации поверхностной площади для создания развертки, которая имеет наименьшее количество сгибов.
- Ограничение: Этот метод основан на установлении правил и ограничений, которые должны соблюдаться при развертке, таких как минимальный радиус сгиба или максимальное количество сгибов на единицу площади.
Видео по теме:
Определение развертки
Разверткой называют плоское изображение какого-либо трехмерного тела, полученное путем его разреза и последующего разложения на плоскость.
Развертка является важным инструментом при проектировании и изготовлении трехмерных объектов. Она позволяет легче визуализировать и понимать форму и размеры объекта, а также упрощает процесс изготовления, так как на плоскости легче отобразить все детали и сегменты объекта.
Развертка используется во многих отраслях, таких как машиностроение, архитектура, текстильная промышленность и т.д.
По сути, развертка представляет собой двумерную карту трехмерного объекта, на которой отображены все детали в соответствующем масштабе и пропорциях. Она может быть представлена как в виде чертежей, так и в виде компьютерных моделей и раскроев.
Виды разверток в математике
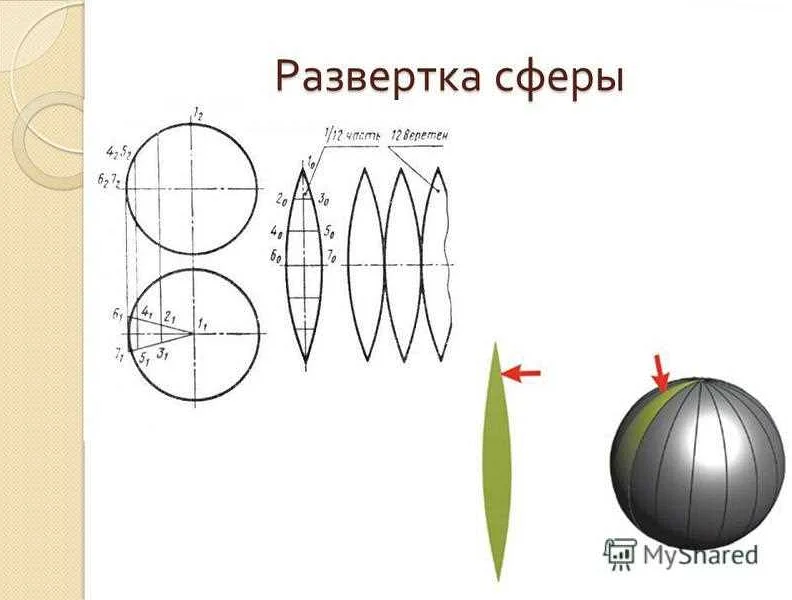
Развертка поверхности – это способ изображения поверхности в плоскости, который основан на ее разглаживании и отображении на плоскость без искажений. Развертку поверхности можно использовать для подсчета площади поверхности и изображения различных геометрических фигур.
Развертка тела – это способ изображения тела в плоскости, который основан на его разбиении на части и отображении каждой части на плоскость без искажений. Развертку тела можно использовать для подсчета объема тела и изображения различных пространственных фигур.
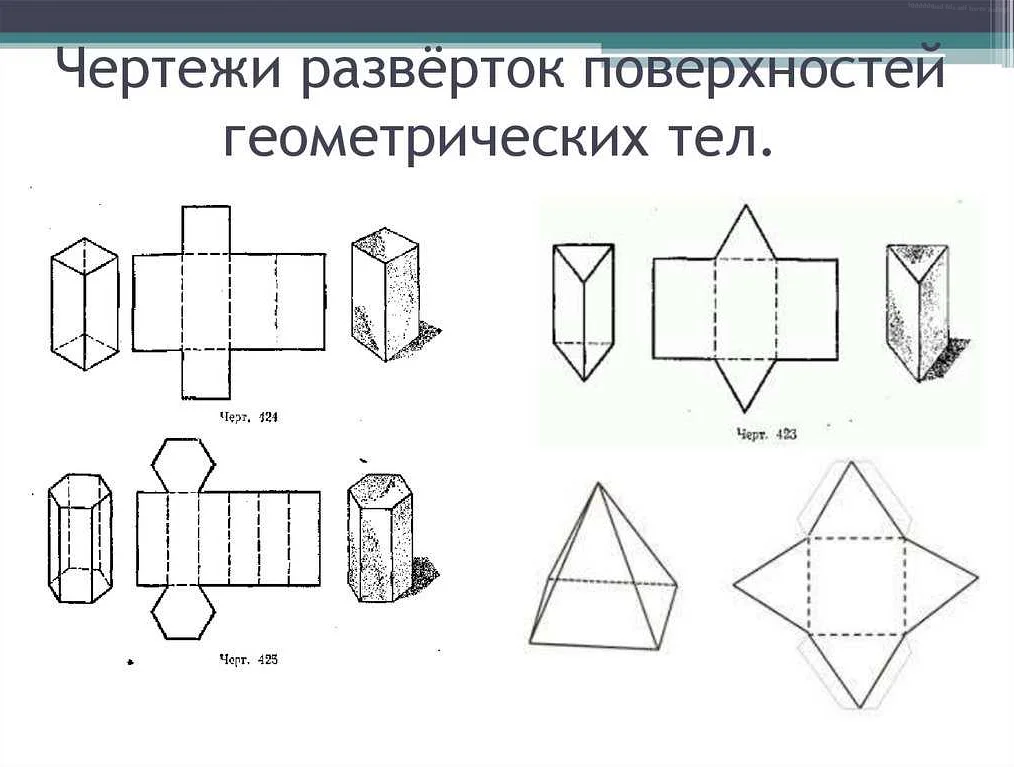
Развертка многогранника – это способ изображения многогранника в плоскости, который основан на разрезании многогранника и его отображении на плоскость без искажений. Развертку многогранника можно использовать для нахождения площади каждой грани многогранника, числа его вершин и ребер, а также для изображения различных многогранников.
Развертка дуги – это способ изображения дуги окружности в плоскости, который основан на ее разбиении на части и отображении каждой части на плоскость без искажений. Развертку дуги можно использовать для нахождения длины дуги и для изображения различных кривых.
Цель и применение развертки
Развертка в математике используется для превращения трехмерного объекта в плоскую фигуру, которую можно использовать для удобного изучения и анализа. При этом сохраняются все геометрические параметры объекта, такие как площадь, периметр и объем.
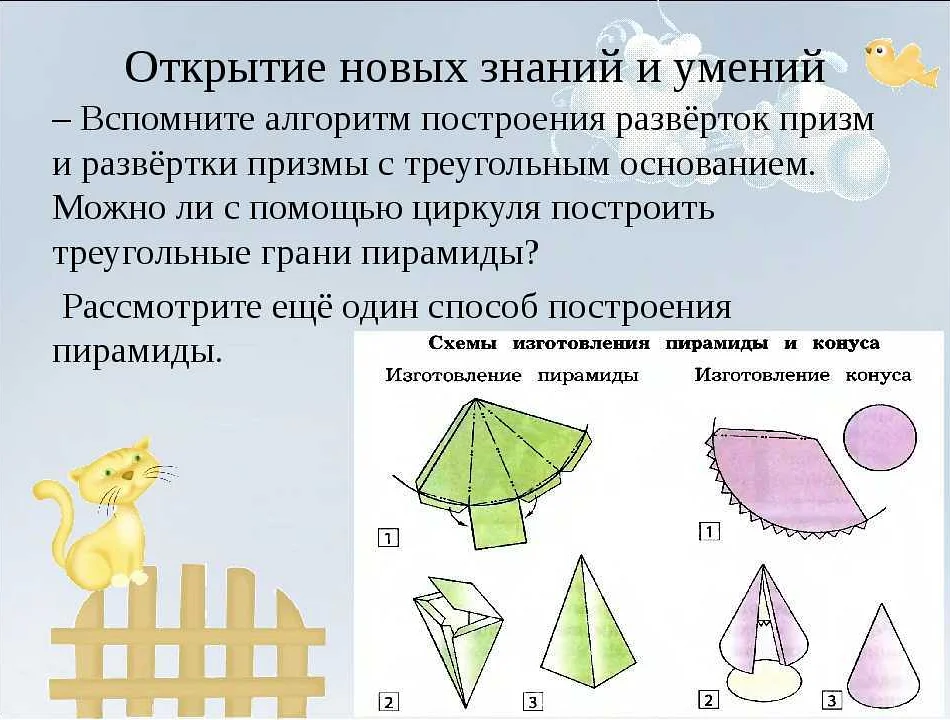
Один из основных применений развертки – это проектирование и изготовление деталей и конструкций, например, бумажной модели здания или автомобиля. Развертка позволяет получить плоские шаблоны, которые при необходимости можно разрезать и использовать для создания трехмерной фигуры.
Кроме того, развертка используется в геометрии для нахождения площади и периметра сложных форм, таких как несколько взаимосвязанных поверхностей, имеющих различную кривизну и угол наклона.
В архитектуре и строительстве развертки используются для проектирования крыш, фасадов, оконных рам и других элементов зданий. Развертки могут быть созданы как вручную, так и с помощью специальных компьютерных программ, которые позволяют быстро и точно расчитывать все геометрические параметры объекта.
- Развертка позволяет получить плоские шаблоны для создания трехмерных фигур.
- Развертка используется для нахождения площади и периметра сложных форм.
- Развертки применяются в архитектуре и строительстве для проектирования крыш, фасадов, оконных рам и других элементов зданий.
Развертка в геометрии
Развертка – это плоская фигура, которую можно изобразить на плоскости, если разрезать и разложить по ее граням многогранник. Этот процесс называется разверткой многогранника.
Развертка многогранника позволяет нам удобно изучать его свойства и многогранную форму. Она позволяет анализировать их свойства без необходимости рассматривать объемную форму многогранника.
Развертка имеет несколько свойств, которые определяют ее форму и размер. Одно из них – это площадь развертки. Она равна сумме площадей всех граней многогранника. Другое свойство – это периметр развертки, который характеризует длину всех граней многогранника.
Многогранники могут быть развернуты по-разному, поэтому может существовать несколько различных разверток одного и того же многогранника. Однако, в теории многогранников доказано, что всегда существует хотя бы одна правильная развертка многогранника.
Методы развертки многогранников используются в различных областях, включая архитектуру, дизайн и инженерное дело.
Развертка поверхностей
Развертка поверхности – это процесс преобразования трехмерной поверхности в плоскость. Это очень полезный метод, который используется в разных областях, таких как инженерия, дизайн, архитектура и т.д. Развертку можно использовать для проектирования и изготовления изделий, нарисовав плоскую схему, которая в последствии будет трансформирована в трехмерную поверхность.
Процесс развертки может быть достаточно сложным, так как некоторые поверхности, например, купол или конус, могут иметь необычную форму. Для того чтобы разложить такую поверхность на плоскую область, необходимо использовать специальные техники математических вычислений.
Существует множество способов развертки поверхностей. Например, один из наиболее распространенных методов – это метод аппроксимации. Он заключается в том, что поверхность разбивается на множество маленьких фрагментов, которые потом каждый разворачиваются в плоскость. Если используется этот метод, то точность развертки будет в основном зависеть от размера фрагментов.
Безусловно, развертка поверхностей очень важна в инженерных программных средах, где необходимо разработать сложные изделия. Также, этот метод может быть использован профессиональными дизайнерами для того, чтобы создавать красивые и сложные объекты, архитекторами для проектирования зданий и других сооружений.
Процесс развертки
Развертка в математике – это процесс преобразования трехмерного объекта в двумерный плоский лист, который может быть распечатан, вырезан и использован для создания оригинальной трехмерной формы.
Для развертки необходимо выполнить следующие действия:
- Выбрать объект, который нужно развернуть.
- Разделить объект на несколько частей, каждая из которых может быть развернутой на плоский лист. Как правило, разделение производится вдоль граней.
- На каждой грани устанавливаются метки, которые позже помогут соединить части формы.
- Далее каждая часть разворачивается на плоский лист.
- Части форм присоединяются в нужном порядке с помощью меток. Это позволяет воссоздать исходную трехмерную форму.
Процесс развертки используется в многих областях, таких как дизайн и производство. Например, при создании упаковок из картона развертка помогает определить необходимую форму и размеры упаковки, а также оценить количество материала, необходимого для ее создания.
Развертка также широко используется в проектировании мебели и других предметов интерьера. С помощью разверток можно создавать более сложные формы и переносить их на материалы, такие как дерево или металл.
Примеры развертки в математике
Разверткой в геометрии называется плоская фигура, полученная путем разрезания и распоковки поверхности. Этот метод позволяет удобно изучать свойства тел и площади их поверхности. Давайте рассмотрим несколько примеров развертки в математике.
1. Развертка и каркас куба. Для того, чтобы получить развертку куба, необходимо разрезать поверхность куба по граням и склеить получившиеся фигуры в плоскость. Развертка куба позволяет удобно изучать площадь его поверхности. Каркас куба позволяет увидеть его объем.
2. Развертка цилиндра. Развертка цилиндра представляет собой прямоугольник, удлиненный по одной из сторон. Она позволяет определить площадь боковой поверхности цилиндра. Развертка также позволяет увидеть, что площадь боковой поверхности цилиндра равна произведению высоты цилиндра на длину развертки.
3. Развертка октаэдра. Октаэдр представляет собой многогранник, состоящий из 8 граней. Развертка октаэдра представляет собой звезду с 8 лучами, расположенными в ряд один за другим. Развертка помогает определить площадь поверхности многогранника и удобно изучать его структуру.
Особенности восстановления тел по разверткам
Развертка в математике является одним из основных способов отображения трехмерных объектов в двухмерной плоскости. После развертки получается плоское изображение, которое называют разверткой.
Восстановление тела по развертке – задача, которая требует знания геометрии и умения работать с развертками. Особенностью процесса восстановления тел по разверткам является то, что трехмерный объект может быть представлен в развертке в разных масштабах, что может привести к ошибкам при восстановлении.
Для того чтобы восстановление проходило без ошибок, необходимо заранее определить масштабирование развертки и ее параметры. Важно также учитывать, что разные части развертки могут иметь разные размеры и ориентацию.
Для получения качественного восстановления тела по развертке необходимо уметь работать с габаритной сеткой, определять углы и расстояния между точками, правильно отображать детали. Без знания геометрии и опыта работы с развертками восстановление тела может стать неточным или даже невозможным.
Итак, восстановление тела по развертке – это непростая задача, требующая от человека знания математики и геометрии, а также опыта работы с развертками. Только зная особенности работы с развертками, можно получить качественное восстановление трехмерного объекта в двумерном пространстве.
Ошибки при развертке
Развертка – это изображение плоской фигуры, которая некоторым образом связана с трехмерной формой. Однако, при выполнении развертки могут возникнуть ошибки, которые могут привести к неверным результатам.
Ошибки при развертке могут возникнуть из-за следующих факторов:
- Неправильных знаний геометрии и пространственной конструкции;
- Плохой качества начальных данных (например, некачественная измерительная оснастка);
- Ошибок в конструкции самой фигуры (например, когда она не симметрична по отношению к своей оси).
Какие ошибки могут возникнуть при развертке:
- Накладывание развертки на саму фигуру;
- Необходимость наложения нескольких частей развертки друг на друга (если фигуры не соответствуют условиям теоремы развертки);
- Отступления от графических условий;
- Проблемы с масштабированием фигуры.
Итог: при выполнении развертки необходимо учитывать все вышеперечисленные факторы и быть внимательным при каждом этапе ее создания, чтобы минимизировать возможные ошибки.
Вопрос-ответ:
Какие виды разверток используются в математике?
В математике используются различные виды разверток: плоские развертки, цилиндрические развертки, конические развертки и сферические развертки. Каждый вид используется в зависимости от того, какую геометрическую фигуру необходимо развернуть.
Каковы особенности плоской развертки?
Плоская развертка представляет собой развернутое изображение трехмерной фигуры на плоскости. Особенностью плоской развертки является то, что при ее изготовлении некоторые углы и стороны фигуры могут быть искажены, поэтому перед изготовлением плоской развертки необходимо тщательно рассчитать размеры каждого элемента для получения точного изображения.
Каковы виды цилиндрических разверток?
В математике используются два вида цилиндрических разверток: прямая цилиндрическая развертка и развертка по спирали (винтовая). Прямая цилиндрическая развертка используется для выкройки деталей, имеющих форму цилиндра, а развертка по спирали применяется при изготовлении конических фигур, таких как конусы и пирамиды.
Как изготавливают конические развертки?
Для изготовления конических разверток необходимо разрезать коническую фигуру по определенной линии и развернуть ее на плоскость. Однако при изготовлении конических разверток требуется быть очень внимательным, так как даже малейшая ошибка при вычислении размеров может привести к искажению изображения конической фигуры.
Можно ли использовать развертку для изготовления мебели?
Да, развертки могут быть использованы для изготовления мебели. Использование разверток позволяет точно рассчитать размеры деталей для мебели, что помогает снизить вероятность ошибок при изготовлении. Кроме того, использование разверток позволяет ускорить процесс изготовления мебели и снизить затраты на материалы.
Можно ли использовать развертку при изготовлении космических кораблей?
Да, развертки могут быть использованы при изготовлении космических кораблей. Использование разверток позволяет точно рассчитать размеры деталей для корабля и определить, какие детали необходимо изготовить заранее для сборки в космосе. Кроме того, использование разверток позволяет сократить затраты на материалы и ускорить процесс изготовления космического корабля.
Как использовать развертку для изготовления кожаных изделий?
Для изготовления кожаных изделий можно использовать развертки, которые позволяют точно рассчитать размеры деталей и их расположение на коже. Для этого необходимо наложить образец детали на кожу и обвести его на ней, затем разрезать и развернуть на плоскость. Использование разверток позволяет значительно снизить затраты на кожу и ускорить процесс изготовления кожаных изделий.






