Решетка в дискретной математике является абстрактной структурой, которая позволяет сравнивать элементы их отношениями порядка. Она используется в различных областях, таких как теория множеств, логика, алгоритмы и другие. В статье подробно рассмотрены основные понятия и примеры применения решеток в математике.
Решетка – это абстрактная математическая модель, используемая в теории категорий и теории порядка. Можно сказать, что на решетке определен упорядоченный набор элементов, удовлетворяющих определенным свойствам. Решетка является дискретной моделью, что означает, что элементы, входящие в решетку, необходимо ограничивать предопределенным множеством значений.
В решетке все элементы имеют как нижнюю, так и верхнюю границы. Отношения частичного порядка на этих границах также являются свойствами решетки. Решетка может использоваться как инструмент для определения математических отношений между объектами, представленными набором общих свойств.
Решетки находят широкое применение в различных областях математики, включая алгебру, геометрию, теорию категорий и теорию порядка. Они также могут использоваться в компьютерных науках, когда необходимо упорядочивать и классифицировать данные.
Решетка дискретной математики
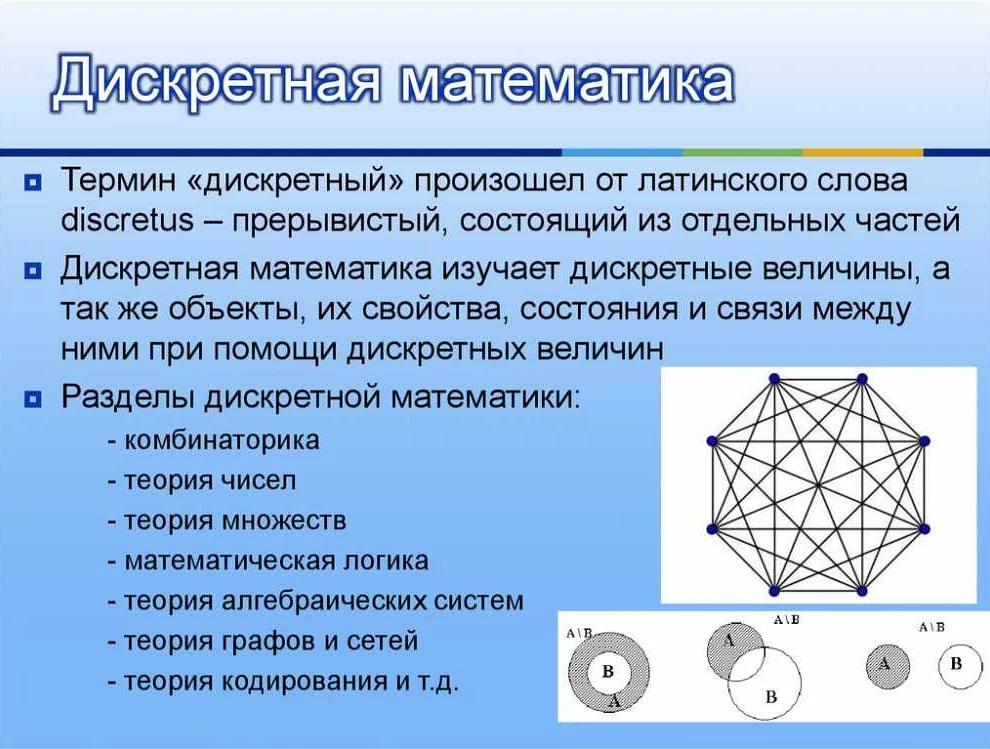
Решетка в дискретной математике – это алгебраическая структура, которая состоит из множества элементов и двух бинарных операций: наименьшего общего кратного и наибольшего общего делителя.
Основная идея решетки заключается в том, что каждый элемент имеет свой наименьший и наибольший элементы (в случае их существования) и все элементы могут быть отсортированы по взаимному порядку. Таким образом, решетка позволяет рассматривать элементы в контексте их отношений.
Решетка используется во многих областях дискретной математики, таких как теория графов, теория кодирования, теория алгоритмов и другие. Кроме того, решетки имеют множество приложений в физике, химии, экономике и других областях естественных наук и гуманитарных наук.
Решетки могут быть классифицированы по различным критериям, таким как размерность, свойства элементов, порядок и другие. Некоторые известные классы решеток включают пространственные решетки, решетки Булевых функций и дистрибутивные решетки.
Понятие решетки
Решетка – это множество, на котором определены две бинарные операции: “наименьший общий предшественник” и “наибольший общий последовательник”.
Каждая решетка состоит из элементов, которые могут быть упорядочены друг относительно друга с помощью подобных операций. Также элементы решетки удовлетворяют определенным свойствам, таким как ассоциативность, коммутативность, идемпотентность и дистрибутивность.
Решетки рассматриваются в различных областях математики, физики, компьютерных наук и других наук для решения задач, связанных с упорядочиванием и классификацией объектов.
Примерами решеток являются частично упорядоченные множества, такие как множество действительных чисел и множество строк, а также алгебраические структуры, такие как линейные пространства и алгебры Буля.
- Основные понятия, связанные с решеткой:
- Элемент решетки;
- Наименьший элемент решетки;
- Наибольший элемент решетки;
- Диаграмма Юнга;
- Супремум и инфимум.
Решетки являются важной темой в дискретной математике и широко используются в анализе и проектировании систем, таких как базы данных, сети, операционные системы и другие.
Элементы решетки
Решетка – это такое множество, на котором определены две операции: супремум и инфимум. Элементы решетки подчиняются двум законам: они ассоциативны (a ∨ (b ∨ c) = (a ∨ b) ∨ c и a ∧ (b ∧ c) = (a ∧ b) ∧ c) и коммутативны (a ∨ b = b ∨ a и a ∧ b = b ∧ a).
Если в решетке каждые два элемента имеют супремум и инфимум, то она называется полной (или дистрибутивной). Но в общем случае в решетке могут быть элементы, не имеющие инфимума или супремума.
Наибольший и наименьший элементы решетки называются соответственно верхней и нижней гранями решетки. В совершенные решетки, которые являются полными и имеют наибольший и наименьший элементы, входят только те элементы, которые можно получить путем объединения и пересечения некоторых элементов решетки.
- Пример совершенной решетки – множество подмножеств конечного множества с операциями объединения и пересечения. В этом случае наибольшим элементом является всё множество, наименьшим – пустое множество. Все элементы, которые можно получить из объединения и пересечения, являются элементами решетки.
- Еще один пример решетки – множество целых чисел с операциями max и min. В этом случае наибольшим элементом является +∞, наименьшим – -∞. Совершенную решетку в этом случае образуют все целые числа.
Решетки широко используются в математике, компьютерных науках и других областях, где необходимо работать с частичным порядком.
Бинарные отношения
Бинарным отношением называется любое подмножество кросс-продукта двух множеств. Есть два типа бинарных отношений: отношение равенства и отношение порядка.
Отношение равенства обозначается как “=” и свойства его такие, как рефлексивность, симметричность и транзитивность. Если мы хотим выразить отношение неравенства, мы используем символ “≠”.
Отношение порядка обозначается как “<” либо “≤”. Отношение “<” обладает такими свойствами, как иррефлексивность, анти-симметричность и транзитивность. Отношение “≤” является рефлексивным, анти-симметричным и транзитивным.
Однако бинарные отношения не ограничиваются только этими двумя типами. Они могут быть какими угодно, например, “предок-потомок” в генеалогическом дереве или “курс-пререквизит” в списке учебных предметов на курсах.
Бинарные отношения могут быть представлены в виде таблицы, где каждый элемент этой таблицы представляет пару элементов из двух множеств. Эти таблицы могут быть представлены в виде матриц, где каждый элемент матрицы представляет значение бинарного отношения.
Частичный порядок
Частичный порядок в теории решеток – это полурешетка, в которой между двумя элементами может быть только сравнение на “больше или равно” или “меньше или равно”. Таким образом, некоторые элементы могут оставаться несравнимыми.
Например, в множестве дробей, если две дроби не могут быть сравнены на “больше или равно” или “меньше или равно”, то они будут несравнимы.
Частичный порядок записывается как отношение порядка на множестве элементов. Оно является рефлексивным, транзитивным и антисимметричным.
- Рефлексивность – каждый элемент сравнивается сам с собой и является не менее “большим” или “меньшим”.
- Транзитивность – если элемент A сравним с элементом B и элемент B сравним с элементом C, то элемент A также сравним с элементом C.
- Антисимметричность – если элемент A сравним с элементом B и элемент B сравним с элементом A, то A и B равны.
Частичный порядок используется для построения решетки, которая является отношением иерархии между элементами.
Примеры решеток

Решетки используются в различных областях математики и дискретной математики в том числе. Решетки могут быть представлены различными способами, включая графические диаграммы, таблицы и матрицы. В этом разделе мы рассмотрим несколько примеров решеток.
Решетка натуральных чисел
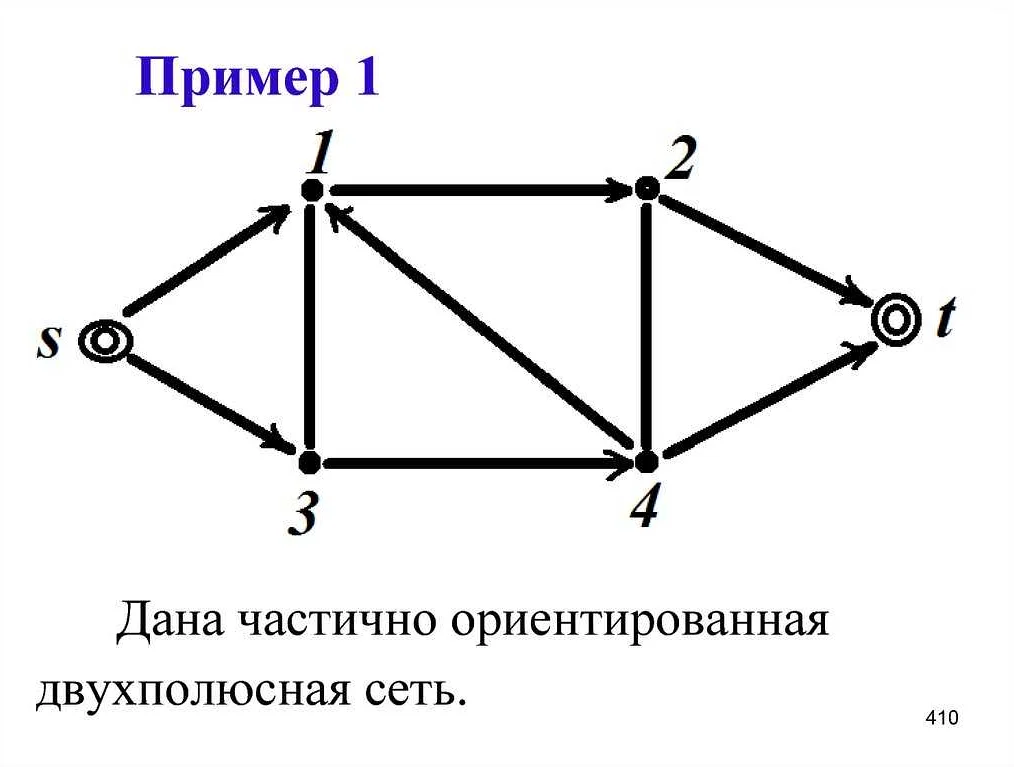
Простой пример решетки – решетка натуральных чисел. В этой решетке каждое число находится выше своих делителей, а ниже своих кратных. Например, число 15 находится ниже чисел 30 и 45, и выше чисел 5 и 3.
Булевы решетки
Булевы решетки состоят из двух элементов, которые мы будем обозначать 0 и 1. Эти элементы могут быть связаны с помощью операций «И» и «ИЛИ». Например, решетка {0, 1} с операцией «И» образует следующую решетку:
| И | 0 | 1 |
| 0 | 0 | 0 |
| 1 | 0 | 1 |
Эта решетка имеет следующие свойства:
- Элемент 1 является верхним элементом решетки.
- Элемент 0 является нижним элементом решетки.
- Операция «И» образует минимум в множестве.
- Операция «ИЛИ» образует максимум в множестве.
Теорема Дедекинда-Макнаба
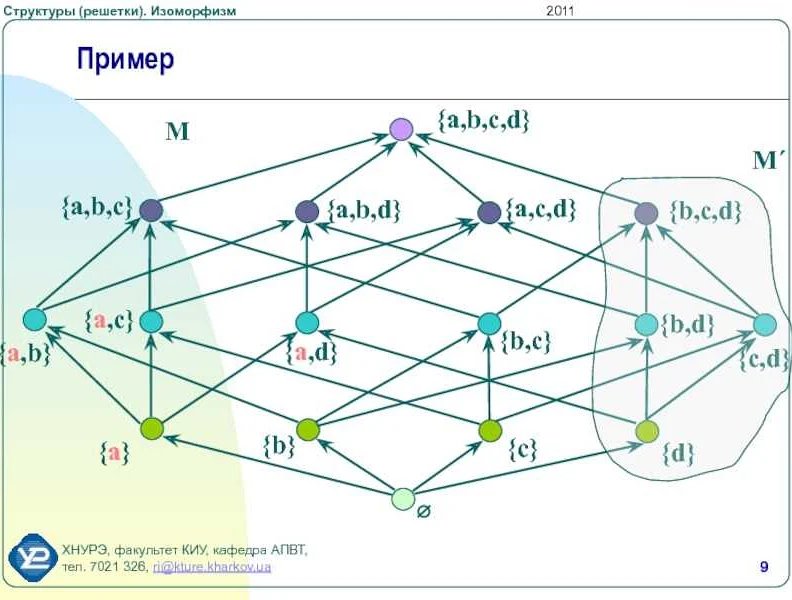
Теорема Дедекинда-Макнаба — это важное утверждение в области дискретной математики, которое гласит, что любое подмножество множества должно быть представлено в форме пересечения непересекающихся прямых.
Данная теорема имеет широкое применение в алгебре и теории чисел, где часто требуется найти базис в пространстве, порожденном некоторым множеством.
Одно из наиболее известных применений теоремы Дедекинда-Макнаба – это разложение любого конечного поля на прямое произведение полей Галуа.
Одним из ключевых факторов, определяющих важность теоремы Дедекинда-Макнаба, является то, что она позволяет обобщить понятие базиса и некоторые другие фундаментальные понятия линейной алгебры на произвольные множества.
Изоморфизм решеток
Изоморфизм решеток – это отображение двух решеток, которое сохраняет порядок элементов. То есть, если два элемента в первой решетке связаны каким-то отношением порядка, то и соответствующие им элементы во второй решетке также связаны этим же отношением порядка.
Изоморфизм решеток позволяет связать различные решетки между собой, даже если они различны по своей природе. Например, можно построить изоморфизм между решеткой подмножеств множества A и решеткой идеалов кольца многочленов в A.
Изоморфизм решеток обладает несколькими важными свойствами. Во-первых, он является биективным отображением, то есть каждому элементу одной решетки соответствует единственный элемент другой решетки и наоборот.
Во-вторых, изоморфизм решеток сохраняет некоторые структурные свойства решеток, такие как наличие наименьшего и наибольшего элементов, расщепляемость и непротиворечивость.
Это свойство изоморфизма решеток позволяет использовать одни решетки для изучения других решеток с аналогичной структурой и заданными связями порядка между элементами.
Потенциалы и атомы
Потенциалы – это особый вид функций, которые используются в физике для описания поля. В дискретной математике потенциалы могут быть использованы для описания различных решеток.
У каждого атома есть потенциал, обусловленный свойствами электронной оболочки. Взаимодействуя друг с другом, атомы образуют кристаллическую решетку, где каждый атом находится в устойчивом равновесном положении, соответствующем минимуму потенциальной энергии системы.
Обычно атомы в кристаллической решетке располагаются в узлах так называемой элементарной ячейки, которая повторяется бесконечное число раз по всему кристаллу. Параметры решетки, такие как длина ребра элементарной ячейки, углы её поворота и количество атомов в ячейке, определяются свойствами вещества, из которого состоит решетка.
Таким образом, понимание понятия потенциалов и атомов в дискретной математике очень важно для понимания структуры кристаллических решеток, что в свою очередь является важным аспектом в материаловедении и физике в целом.
Применение решеток в математике и информатике
В математике решетки широко используются для изучения порядка и связей между элементами в множествах. Например, на решетке можно определить отношение частичного порядка, когда каждый элемент имеет свое место и соответствующие связи с другими элементами. Это позволяет более точно определять свойства и отношения между элементами.
В информатике решетки также находят широкое применение. Они могут быть использованы для моделирования процессов в системах, анализа и оценки качества программ и алгоритмов. Например, решетки могут быть использованы при анализе времени исполнения программы, при поиске ошибок и оптимизации алгоритмов.
Кроме того, решетки нашли свое применение при проектировании баз данных и при работе с логическими исчислениями. Они позволяют более эффективно управлять данными и принимать решения на основе логических заключений.
В целом, решетки представляют собой важный инструмент в математике и информатике, который позволяет более точно определять свойства и отношения между элементами в разных системах и является важным элементом при моделировании и анализе сложных процессов.
Дальнейшие исследования решеток
Решетки являются важной разновидностью алгебраических структур, которые находят применение в различных областях математики и computer science. Современные исследования решеток открывают новые возможности для их применения в различных областях, таких как социальная и информационная наука, физика, химия и экономика.
Среди актуальных направлений исследований решеток можно выделить теорию полурешеток, которая изучает подкласс решеток, отвечающих специальным аксиомам. Также находятся в фокусе внимания исследования конечных решеток, которые имеют ограниченный размер и находят применение в задачах оптимизации и дискретной оптимизации.
Другое направление исследования решеток – это использование теории решеток в криптографии и безопасности информации. Бинарные решетки при этом служат в основном для построения криптосистем на основе задачи о решетках, которая является сложной вычислительной проблемой, найти решение которой вычислительно сложно.
В целом, исследования решеток продолжаются в нескольких областях математики и computer science, и новые результаты могут иметь отношение к применениям в различных отраслях науки и промышленности.






