Шпаргалки для подготовки к ОГЭ по математике с кратким изложением основных тем и понятий, приведением формул и правил, которые помогут облегчить процесс изучения и повысить успеваемость школьника.
ОГЭ по математике – это один из самых важных экзаменов, который сдают российские школьники. Он не только определяет уровень знаний и навыков ученика, но и влияет на возможность поступления в учебное заведение.
На экзамене ученикам предстоит решить множество задач на различные темы: от арифметики и геометрии до алгебры и функций. Для того чтобы успешно справиться с этими задачами, ученикам нужно знать не только теорию, но и уметь применять ее на практике.
В этой статье мы расскажем о том, какие шпаргалки помогут на ОГЭ по математике. Они позволят быстро найти нужную формулу или правило и не терять времени на поиск ответа на задачу.
Шпаргалки для огэ по математике
ОГЭ по математике — это ответственное событие для каждого школьника. Важно не только понимать материал, но и уметь его применять на практике. Шпаргалки могут очень помочь в подготовке к экзамену. Мы собрали несколько полезных советов, которые помогут вам успешно сдать ОГЭ по математике.
1. Список формул
Составьте список формул и примеров, которые вы должны знать наизусть. Разбейте их на блоки в зависимости от темы. Запишите этот список на бумаге или в электронном виде, чтобы иметь под рукой.
2. Законы арифметики
Помните, что законы арифметики являются основой математики. Освойте их наизусть, чтобы быстро решать задачи. Разбейте их на блоки и тренируйтесь в их применении.
3. Графики функций
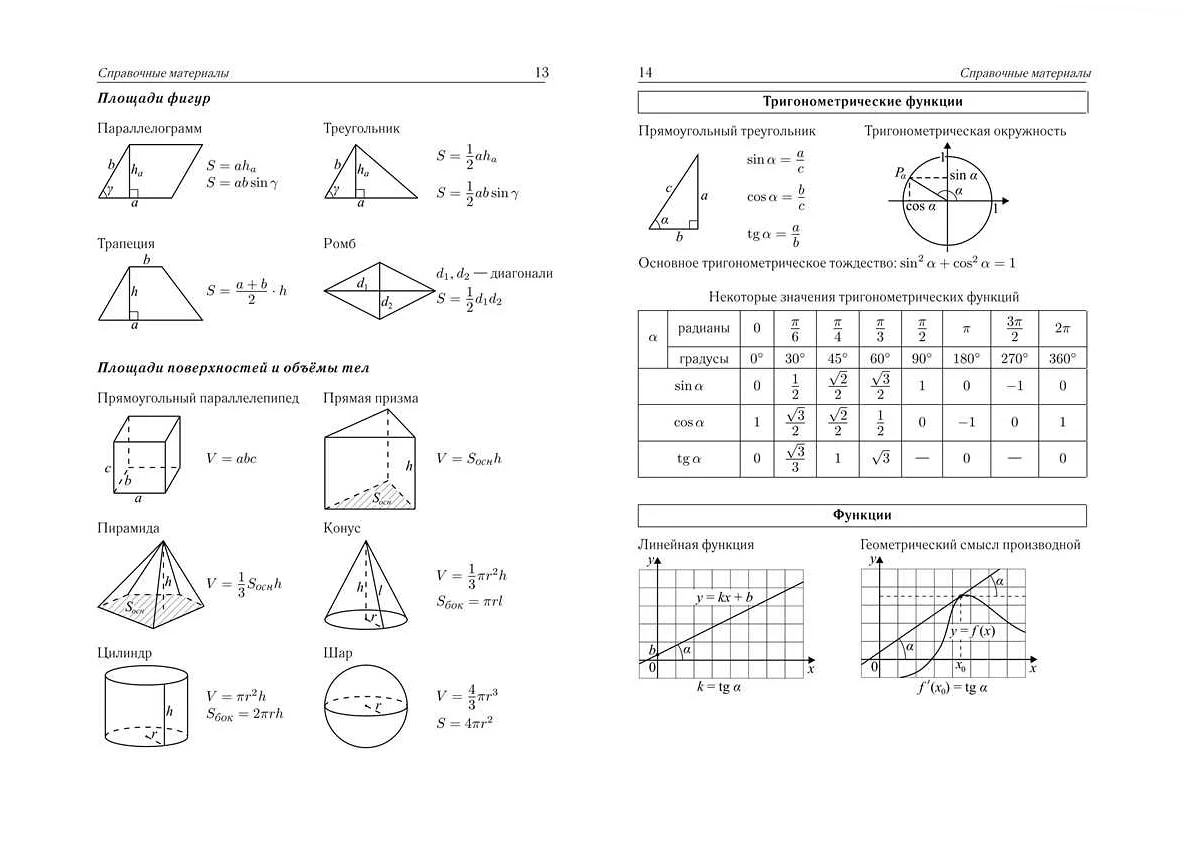
Графики функций являются важной темой для ОГЭ по математике. Составьте список функций и их графиков и тренируйтесь в их решении. Запомните основные типы графиков, такие как линейный, экспоненциальный, логарифмический, квадратичный.
4. Геометрия
Геометрия является одной из важнейших тем в математике. Советуем составить список основных теорем и понятий. Изучить основные понятия: перпендикуляр, параллель, угол, равнобедренный треугольник, прямоугольный треугольник. На основе этих понятий можно решить многие задачи.
5. Повторение и тренировка
Для успешной подготовки к ОГЭ необходимо много тренироваться и повторять материалы. Решайте много задач, используя шпаргалки, которые вы составили. Это поможет закрепить материал и улучшить вашу производительность.
Зачем нужны шпаргалки
Шпаргалки – это небольшие карточки, справочники или таблицы, которые содержат основные понятия и формулы, необходимые для определенной темы или предмета. Они могут помочь ученику быстро ориентироваться в материале и запомнить ключевые моменты без излишнего напряжения мозга.
Польза шпаргалок:
- Экономят время: когда ученик уверен в том, что находит нужную информацию мгновенно, он экономит время на поиск необходимых фактов и не теряет баллы за медлительность;
- Улучшают результаты: кратые и четкие шпаргалки могут помочь контролировать эмоциональное состояние во время экзамена, что позволяет сохранить уверенность, а также положительно отразиться на общем результате;
- Помогают запомнить формулы: шпаргалки с формулами могут помочь студенту быстро выучить необходимые формулы и правила без излишней траты времени.
Кроме того, шпаргалки могут быть полезными на протяжении всего года, когда ученик изучает новые темы и материалы.
Шпаргалки для алгебры
Алгебра – это один из основных разделов математики, на который стоит уделить особое внимание при подготовке к ОГЭ. Чтобы помочь вам упорядочить знания и быстрее решать задачи на экзамене, мы подготовили несколько шпаргалок.
1. Базовые формулы: умножения скобок, раскрытия скобок, степенные и корневые функции, формулы суммирования и разностей кубов и квадратов.
2. Таблица умножения: помните таблицу умножения до 10, это позволит быстрее решать задачи и проверять ответы.
3. Определения и свойства: линейная и квадратичная функции, системы уравнений и неравенств, геометрические фигуры и их свойства.
4. Список часто встречающихся типовых задач: построение уравнений, решение уравнений и неравенств, решение систем, определение координат точек на графиках.
5. Реализация алгоритма: умение последовательно выполнять действия по решению задач, разбивая их на более мелкие этапы.
В заключении, следует отметить, что эти шпаргалки не заменят полноценной подготовки и тренировок. Но они могут помочь вам упорядочить свои знания и быстрее решать задачи на экзамене.
Шпаргалки для геометрии
Основные теоремы:
- Теорема Пифагора: a2 + b2 = c2
- Теорема косинусов: a2 = b2 + c2 – 2bc cos A
- Теорема синусов: a / sin A = b / sin B = c / sin C
- Теорема о равенстве угловых сумм: сумма углов треугольника равна 180 градусам
Формулы для площади фигур:
- Площадь прямоугольника: S = a * b
- Площадь треугольника: S = (b * h) / 2
- Площадь трапеции: S = ((a + b) * h) / 2
- Площадь круга: S = π * r2
Формулы для вычисления геометрических параметров:
- Периметр прямоугольника: P = 2a + 2b
- Периметр треугольника: P = a + b + c
- Периметр круга: P = 2πr
Дополнительные шпаргалки:
ФигураФормула
| Ромб | S = D1 * D2 / 2 |
| Параллелограмм | S = a * h |
| Равнобедренная трапеция | S = ((a + b)/2) * h |
Шпаргалки для статистики
Статистика – это взаимосвязанная система методов для сбора, анализа и интерпретации данных. Важно знать основные понятия и формулы, чтобы успешно сдать ЕГЭ по математике. Ниже представлены некоторые шпаргалки, которые помогут вам запомнить основные формулы и определения.
Основные понятия:
- Среднее арифметическое: сумма всех элементов выборки, поделенная на их количество. Формула: Xср = (x1 + x2 + … + xn) / n.
- Стандартное отклонение: это мера разброса данных в выборке. Формула: σ = √∆²/n, где ∆² – дисперсия, n – количество элементов в выборке.
- Корреляция: статистическая мера зависимости между двумя переменными. Коэффициент корреляции Пирсона вычисляется по формуле: r = (Σxy – ΣxΣy/n) / (√(Σx² – (Σx)²/n) * √(Σy² – (Σy)²/n)).
Основные формулы:
- Формула Байеса: Р(А|В) = P(B|A) * P(A) / P(B).
- Формула Симпсона: ∫a,b f(x)dx ≈ (b-a)/6 * (f(a) + 4f((a+b)/2) + f(b)).
- Формула Пуассона: P(x) = (e^-λ * λ^x) / x!, где x – число событий, λ – среднее число событий.
Пример задания:
XYZ
| 2 | 4 | 6 |
| 3 | 5 | 7 |
| 4 | 5 | 9 |
Найти:
- Среднее арифметическое для Y.
- Стандартное отклонение для Z.
- Коэффициент корреляции Пирсона между X и Y.
Решение:
- Xср = (4 + 5 + 5) / 3 = 4.67.
- Δ² = ((6-4.67)² + (7-4.67)² + (9-4.67)²) / 3 ≈ 3.11, σ = √3.11 ≈ 1.76.
- r = ((2-4.67)*(4-4.67) + (3-4.67)*(5-4.67) + (4-4.67)*(5-4.67)) / (√((2²+3²+4²)-(2+3+4)²/3) * √((4²+5²+5²)-(4+5+5)²/3)) ≈ -0.41.
Шпаргалки для измерения
Линейка: используется для измерения длинных предметов. Обычно имеет метки в сантиметрах и миллиметрах.
Угольник: используется для измерения углов. Обычно имеет метки 90, 45 и 30 градусов.
Штангенциркуль: используется для точного измерения размеров предметов. Обычно имеет две шкалы – основную и дополнительную.
Электронные весы: используются для измерения массы предметов. Обычно имеют жидко-кристаллический дисплей, на котором выводится масса.
Мерный стакан: используется для измерения жидкостей. Обычно имеет метки в миллилитрах.
- Совет: перед использованием инструментов для измерения, убедитесь, что они правильно откалиброваны.
- Совет: при измерении длинных предметов, всегда прижимайте линейку к ним плотно.
- Совет: при измерении углов, всегда помещайте угольник на плоскость, чтобы избежать погрешностей из-за наклона.
ИнструментЧто измеряетКак использовать
| Линейка | Длину предмета | Прижмите линейку плотно к предмету |
| Угольник | Углы | Поместите угольник на плоскость, чтобы избежать погрешностей из-за наклона |
| Штангенциркуль | Точные размеры предмета | Проверьте откалиброванность и используйте обе шкалы для более точных измерений |
| Электронные весы | Массу предмета | Поместите предмет на весы, подождите, пока они вычислят массу |
| Мерный стакан | Объем жидкости | Заливайте жидкость в мерный стакан до нужной метки |
Шпаргалки для функций
Функции обратного отношения:
- Обозначаются как f-1(x)
- Задаются условиями: y = f(x) и x = f-1(y)
- График функции и ее обратной функции симметричны относительно прямой y=x
Функции вида y = kx + b:
- Выражаются в общем виде как y = f(x) = kx + b
- k – коэффициент наклона, b – свободный член
- График функции является прямой, если k ≠ 0
- Если k = 0, то функция является константой f(x) = b и ее график – горизонтальная прямая
Тригонометрические функции:
- sin θ/cos θ = tan θ
- cos θ/sin θ = cot θ
- sin2 θ + cos2 θ = 1
- cos(π/2 – θ) = sin θ, sin(π/2 – θ) = cos θ, tan(π/2 – θ) = cot θ
- График функции sin x – это периодическая кривая с периодом 2π
Степенные функции:
- Функции вида f(x) = xn, где n – натуральное число
- График функции изменяет направление в точке (0,0) в зависимости от четности/нечетности n
- При n > 1 график функции возрастает при x > 0 и убывает при x < 0
- При n < 1 график функции возрастает при x > 0 и стремится к оси x при x → ∞ и x → -∞
Шпаргалки для уравнений

Уравнения – это математические выражения, в которых неизвестным является одна или несколько величин, называемых переменными. Решение уравнений является важной частью математической подготовки.
Существуют различные методы решения уравнений, включая метод подстановки, метод равных коэффициентов и метод факторизации. Одним из ключевых шагов в процессе решения уравнения является приведение его к стандартному виду.
- Уравнения вида ax + b = 0. Решение: x = -b/a.
- Квадратные уравнения вида ax2 + bx + c = 0. Решение: x = (-b ± √b2 – 4ac) / 2a.
- Системы уравнений – это группы двух или более формул, которые представляют собой уравнения. Они могут быть решены методом замены или методом сложения и вычитания.
Важно запомнить общие правила решения уравнений, такие как сбалансирование уравнения, использование правил алгебры и контроль полученных ответов путем подстановки.
Общий вид уравненияРешение
| ax + b = c | x = (c – b) / a |
| a(x – b) = c | x = (c / a) + b |
| ax2 + bx + c = 0 | x = (-b ± √b2 – 4ac) / 2a |
Использование шпаргалок для уравнений может помочь ученикам быстрее и точнее решать задачи на экзаменах и тестах, а также обеспечить полное понимание процесса решения уравнений.
Шпаргалки для графиков
1. Графики элементарных функций
- Функции: y = kx + b, y = k/x, y = kx^2, y = √x, y = sin(x), y = cos(x).
- Особенности: симметрия, периодичность, ограниченность.
- Точки: экстремумы (максимумы и минимумы), нули функций, точки пересечения графиков.
2. Графики линейных уравнений
- Уравнение прямой: y = kx + b, где k – угловой коэффициент, а b – свободный член.
- Особенности: наклон, направление, точка пересечения с осью y.
- Построение: через точку и угловой коэффициент, через две точки, через уравнение перпендикуляра к прямой.
3. Графики квадратных уравнений
- Уравнение параболы: y = ax^2 + bx + c, где a ≠ 0.
- Особенности: вершина параболы, ось симметрии, направление ветвей.
- Точки: вершина параболы, нули функции, точки пересечения с осями координат.
4. Использование таблицы значений
- Создание: вводим значения x, находим соответствующие значения y.
- Применение: находим точки на графике, определяем особенности функций, анализируем их поведение.
5. Планирование графиков
- Определение задачи: какая информация должна быть представлена на графике?
- Выбор типа графика: какой тип графика лучше всего подходит для данной задачи?
- Выбор масштаба: как выбрать масштаб, чтобы передать всю необходимую информацию?
- Построение: сначала строим оси координат, затем график функции.
Сокращения и обозначения для графиков
| abs | абсцисса |
| ord | ордината |
| max | максимум |
| min | минимум |
| int | интервал |
| sin | синус |
| cos | косинус |
| tan | тангенс |
Шпаргалки для теории вероятностей
Теорема сложения вероятностей: Вероятность наступления хотя бы одного из событий A и B равна сумме вероятностей наступления каждого из этих событий, вычтенной их общей вероятности наступления. P(A \cup B) = P(A) + P(B) – P(A \cap B).
Теорема умножения вероятностей: Вероятность наступления двух независимых событий A и B равна произведению их вероятностей. P(A \cap B) = P(A) * P(B).
Принцип включений-исключений: Для любых событий A и B вероятность наступления хотя бы одного из этих событий равна сумме вероятностей наступления каждого из них, вычтенной вероятности наступления обоих событий. То есть P(A \cup B) = P(A) + P(B) – 2P(A \cap B).
Биномиальное распределение: Используется для расчёта вероятности наступления события A в n независимых испытаниях с вероятностью p. Формула: P(A) = C^n_k * p^k * q^(n-k), где C^n_k это количество сочетаний.
Формула Байеса: Используется для определения вероятности наступления события A при условии, что произошло событие B. P(A|B) = P(B|A) * P(A) / P(B).
Формула Пуассона: Используется для расчёта вероятности наступления события A в случае, когда количество испытаний стремится к бесконечности, а вероятность наступления события очень мала. Формула: P(A) = λ^k * e^(-λ) / k!, где λ – среднее количество наступлений события A за единицу времени, k – количество наступлений A за некоторый интервал времени.
Как использовать шпаргалки
1. Подготовься заранее
Не оставляй изучение шпаргалок на последний момент – начинай знакомиться с ними еще за несколько дней до теста. Изучай шпаргалки по одной теме в день, чтобы не перегружать свой мозг.
2. Выдели самое важное
Перед тем, как использовать шпаргалку на огэ по математике, обязательно отметь самые важные сведения, которые помогут тебе решить задание. Подчеркивай формулы и другие ключевые слова, чтобы не потерять нужную информацию в шуме.
3. Создай свою шпаргалку
Чтобы запомнить формулы и другие сведения, создай свою собственную шпаргалку. Напиши на бумаге или в блокноте самые важные сведения, которые приходят на ум. Это поможет тебе не только запомнить материал, но и разобраться в теме лучше.
4. Не забудь про контекст
Помни, что сама шпаргалка не решит за тебя задание – тебе нужно использовать ее в контексте задачи. Анализируй задание, пойми, какая формула или сведение сможет помочь тебе решить его. Только так шпаргалка будет действительно полезной.
5. Не забывай про овладение темой
Использование шпаргалок должно быть временным решением, чтобы помочь тебе справиться с заданием на огэ по математике. Но чтобы действительно успешно справляться с тестами, старайся овладеть темой изучения. Это поможет тебе уверенно решать задания, не только на огэ, но и в дальнейшем.
Вопрос-ответ:
Какие шпаргалки подходят для подготовки к ОГЭ по математике?
Существует множество шпаргалок на ОГЭ по математике, некоторые из них можно найти в интернете, другие можно купить в магазинах канцелярских товаров или в онлайн-магазинах. Некоторые из наиболее популярных шпаргалок: “Шпаргалка по математике. ОГЭ”, “Шпаргалка по математике для подготовки к ОГЭ и ЕГЭ”, “Шпаргалка по математике для ОГЭ”.
Как использовать шпаргалки для подготовки к ОГЭ по математике?
Для использования шпаргалок для подготовки к ОГЭ по математике, необходимо сначала ознакомиться с содержимым каждой из них. После этого необходимо выбрать наиболее подходящую шпаргалку для своих нужд и изучить ее содержание. Для лучшего эффекта рекомендуется использовать шпаргалки в сочетании с другими методиками подготовки к ОГЭ по математике, например, решением тестовых заданий или изучением теории.
Какие темы математики можно найти в шпаргалках для ОГЭ?
Шпаргалки для ОГЭ по математике обычно содержат информацию об основных темах математики, которые входят в программу ОГЭ. Среди таких тем: алгебра, геометрия, математический анализ, комбинаторика. Кроме того, шпаргалки могут содержать ключевые понятия и формулы, которые помогут быстрее решить задания по математике.
Могут ли шпаргалки быть единственным способом подготовки к ОГЭ по математике?
Шпаргалки не могут быть единственным способом подготовки к ОГЭ по математике. Шпаргалки представляют собой компактный и удобный источник информации, но для успешной подготовки необходимо изучать теорию и решать задания, чтобы укрепить свои знания и навыки. Шпаргалки могут быть хорошим дополнением к основным материалам и позволить вспомнить теорию и формулы на практике.
Как выбрать наиболее подходящую шпаргалку для ОГЭ по математике?
Чтобы выбрать наиболее подходящую шпаргалку для ОГЭ по математике, необходимо учитывать свой уровень знаний, свои потребности и предпочтения. Некоторые шпаргалки могут содержать необходимый объем информации для прохождения ОГЭ, а другие могут быть более подробными и содержать более широкий круг знаний. Рекомендуется ознакомиться с различными вариантами шпаргалок и выбрать наиболее подходящую для своих нужд.
Могут ли шпаргалки помочь решить сложные задания по математике на ОГЭ?
Шпаргалки могут помочь решить сложные задания по математике на ОГЭ, если в них содержатся необходимые формулы и идеи для решения задач. Однако, для успешного решения заданий на ОГЭ по математике необходимо не только знать формулы, но и уметь подбирать правильные действия для решения задачи. Поэтому, рекомендуется использовать шпаргалки в сочетании с решением тестовых заданий и изучением теории математики.
Где можно найти бесплатные шпаргалки для подготовки к ОГЭ по математике?
Бесплатные шпаргалки для подготовки к ОГЭ по математике можно найти в интернете на специализированных ресурсах для учебы, на форумах и в блогах. Кроме того, существуют приложения для смартфонов и планшетов, в которых можно бесплатно найти шпаргалки и другие материалы для подготовки к ОГЭ по математике. Однако, стоит помнить, что бесплатные материалы могут быть менее качественными, чем платные.
Где найти дополнительную информацию
Если вам не хватает материалов для подготовки к ОГЭ по математике, то рекомендуется обратиться к следующим источникам:
- Учебники – есть много учебников по математике, которые помогут в подготовке к ОГЭ. Например, “Математика. 9 класс. Методические рекомендации и задания для подготовки к ОГЭ”, “Всеобщая история. 9 класс. ОГЭ. Тренировочные задания”, “Русский язык. ОГЭ 2019. Тренировочные задания”.
- Интернет – на многих сайтах есть разнообразные материалы для подготовки к ОГЭ по математике. Можно найти видеоуроки, тесты и тренировочные задания. Например: “ОГЭ по математике” на сайте Экзамен.ру, “ОГЭ по математике” на сайте ЕГЭ-онлайн, “Решаем ОГЭ по математике” на сайте КЕШ.
- Дополнительные уроки – можно обратиться к дополнительным урокам в школе или найти репетитора, который поможет в подготовке к ОГЭ. Вам помогут разобраться в темах, которые вызывают наибольшие трудности и дадут дополнительные материалы для подготовки.
- Проверочные работы и задания из архива ОГЭ – можно найти предыдущие задания ОГЭ на сайте ФИПИ. Решение этих заданий поможет получить представление о трудностях предстоящего экзамена.






