Статья рассказывает о понятии стороны квадрата в математике и как ее можно вычислить. Вы узнаете о свойствах сторон квадрата и их взаимосвязи с другими параметрами, а также о применениях сторон квадрата в повседневной жизни.
Квадрат является одной из самых простых и понятных геометрических фигур, которая обладает рядом интересных свойств. Одно из таких свойств – это сторона квадрата.
Сторона квадрата – это отрезок, который соединяет две противоположные вершины квадрата и является его главной характеристикой. Сторона квадрата также равна длине всех его сторон и определяет его площадь и периметр.
В математике сторона квадрата играет важную роль во многих областях, включая геометрию, алгебру и теорию чисел. Знание стороны квадрата позволяет решать задачи на нахождение площади и периметра, а также нахождение объема при трехмерном представлении куба.
Определение квадрата и его частей

Квадрат – это фигура в геометрии, имеющая четыре равные стороны и четыре угла прямого угла. Каждая сторона квадрата является линией, которая начинается и заканчивается в каждой из вершин квадрата.
Квадрат имеет несколько частей. Одна из его частей – это сторона. Сторона квадрата является линией, которая устанавливает границу между внутренней и внешней областями квадрата. Во всех квадратах все его стороны и углы равны между собой.
Еще одной частью квадрата является диагональ. Диагональ – это линия, которая соединяет две противоположные вершины квадрата. Диагональ проходит через центр квадрата и одновременно делит его на два равных треугольника.
Также квадрат может быть разделен на четыре прямоугольника, два из которых являются большими, а два – маленькими. Большие прямоугольники – это два противника квадрата, объединенные диагональю, а маленькие прямоугольники – это две четверти квадрата, противоположные со стороны диагонали.
Видео по теме:
Что такое сторона квадрата
Строго говоря, квадрат – это такая фигура, у которой все стороны равны друг другу и все углы прямые. И мы можем говорить о длине любой из этих сторон как о “стороне квадрата”.
Отличительной чертой стороны квадрата является её равенство со всеми другими сторонами квадрата. Иными словами, если у нас есть квадрат с длиной стороны 5 см, то мы можем с уверенностью сказать, что все остальные три стороны также равны 5 см.
Для удобства и точности обычно принято обозначать длину стороны квадрата буквой “a”. Таким образом, можно записать формулу для нахождения площади квадрата: S = a² (площадь равна квадрату длины стороны).
Квадраты имеют широкое применение в математике и естественных науках, например, в геометрии, физике, статистике и т.д.
Как найти сторону квадрата
Квадрат – это геометрическая фигура, у которой все стороны равны друг другу. Поэтому, если мы знаем длину одной стороны квадрата, мы можем вычислить длину всех остальных сторон.
Существует несколько способов найти сторону квадрата:
- Использование периметра
Для нахождения стороны квадрата по периметру нам нужно знать его значение. Периметр квадрата равен сумме длин всех его сторон. Для того чтобы найти длину одной стороны квадрата, нужно поделить периметр на 4: a = P/4.
- Использование площади
Площадь квадрата вычисляется по формуле: S = a², где S – площадь, а – длина стороны квадрата. Чтобы найти длину стороны по площади, нужно извлечь корень из площади: a = √S.
- Использование диагонали
Диагональ квадрата – это отрезок, соединяющий противоположные вершины. Если мы знаем длину диагонали, то можем найти длину стороны, используя формулу: a = d/√2, где a – длина стороны, d – длина диагонали.
Зная любой из перечисленных параметров, мы можем легко найти длину стороны квадрата и использовать эту информацию для решения задач геометрии.
Вопрос-ответ:
Что такое сторона квадрата?
Строго говоря, сторона квадрата – это один из четырех равных отрезков, образующих этот квадрат.
Как найти длину стороны квадрата, если известен его периметр?
Длину стороны квадрата можно найти, разделив периметр на 4. То есть, если периметр квадрата равен P, то длина его стороны будет равна P/4.
Какой формулой можно посчитать площадь квадрата, если известна длина его стороны?
Площадь квадрата равна квадрату длины его стороны. То есть, если сторона квадрата равна a, то площадь квадрата будет равна a^2.
Могут ли быть стороны квадрата дробными числами?
Строго говоря, нет. Стороны квадрата должны быть положительными числами, поэтому они не могут быть дробными.
Какова формула нахождения диагонали квадрата, если известна длина его стороны?
Длину диагонали квадрата можно найти, умножив длину его стороны на √2. То есть, если сторона квадрата равна a, то длина его диагонали будет равна a√2.
Может ли квадрат иметь диагональ большую, чем его сторона?
Нет, никогда. Диагональ квадрата всегда будет меньше, чем удвоенная длина его стороны.
Какова площадь квадрата со стороной в 8 см?
Площадь квадрата со стороной в 8 см будет равна 64 кв. см.
Свойства стороны квадрата
1. Одна сторона – все стороны
Квадрат имеет все стороны одинаковой длины. Это означает, что если известна длина одной стороны, можно вычислить длину всех остальных сторон.
2. Стороны перпендикулярны
Стороны квадрата перпендикулярны друг другу, т.е. они образуют угол в 90 градусов.
3. Сторона как диагональ прямоугольника
Строим прямоугольник, у которого одна сторона – это сторона квадрата. Тогда диагональ этого прямоугольника будет равна длине стороны квадрата умноженной на корень из 2.
4. Площадь квадрата считается по формуле
Площадь квадрата равна квадрату длины его стороны: S = a²
5. Периметр квадрата считается по формуле
Периметр квадрата равен сумме длин всех его сторон: P = 4a
6. Разность квадратов
Разность квадратов длин двух смежных сторон квадрата равна удвоенной площади квадрата, образованного на диагонали квадрата.
7. Длина окружности
Длина окружности, вписанной в квадрат со стороной a, равна 4a.
8. Сумма квадратов сторон
Сумма квадратов длин сторон квадрата равна удвоенной площади квадрата: a² + a² + a² + a² = 2a² + 2a² = 4a².
Отношение периметра квадрата к его стороне
Квадрат является одной из базовых фигур в геометрии. Оно определяется четырьмя равными сторонами и углами, которые равны 90 градусам. Каждая сторона квадрата имеет равную длину, которая обозначается как “a”.
Периметр квадрата – это сумма всех его сторон, которая выражается формулой P = 4a. Другими словами, периметр квадрата равен удвоенной длине его стороны, P=2 * a + 2 * a.
Отношение периметра квадрата к его стороне можно представить в виде дроби: P/a = (2 * a + 2 * a) / a. Упрощая эту дробь, получим P/a = 4. То есть, отношение периметра квадрата к его стороне всегда равно 4.
Это свойство может быть полезно при решении геометрических задач, связанных с квадратами, например, при определении периметра или площади квадрата по известной стороне. Зная любую из этих величин, можно легко определить другую, используя формулы, которые базируются на данном соотношении.
Отношение площади квадрата к его стороне
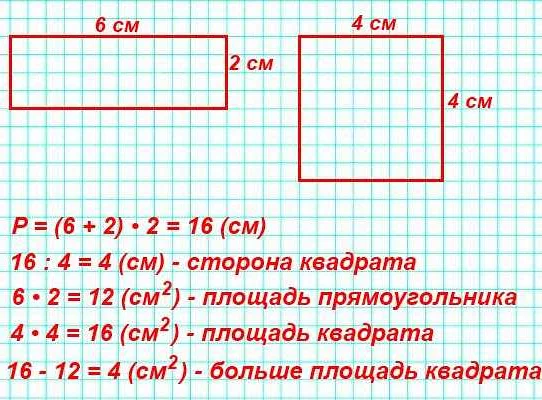
В математике площадь квадрата рассчитывается как квадрат его стороны. Из этого следует, что сторона квадрата является квадратным корнем из его площади. Другими словами, чтобы найти длину стороны квадрата, необходимо извлечь квадратный корень из его площади:
сторона квадрата = √площадь квадрата
С другой стороны, чтобы найти площадь квадрата, необходимо возвести его сторону в квадрат:
площадь квадрата = (сторона квадрата)²
Отношение площади квадрата к его стороне можно выразить следующим образом:
- Если увеличить длину стороны квадрата в 2 раза, то его площадь увеличится в 4 раза;
- Если уменьшить длину стороны квадрата в 2 раза, то его площадь уменьшится в 4 раза;
- При изменении длины стороны квадрата в n раз, его площадь изменится в n² раз;
- При изменении площади квадрата в n раз, длина его стороны изменится в √n раз.
Отношение площади квадрата к его стороне является важным концептом в геометрии и имеет множество применений в физике, инженерии и других областях науки и техники.
Примеры решения задач на нахождение стороны квадрата
Знание формулы для нахождения стороны квадрата, а также умение применять её на практике, позволяет успешно решать задачи с данным геометрическим фигурами.
Пример 1:
Дан квадрат, периметр которого равен 40 см. Найдите значение стороны квадрата.
Решение:
Пусть x – искомое значение стороны квадрата. Тогда по формуле периметра квадрата 4x = 40. Разделим обе части уравнения на 4:
x = 10 см
Итак, сторона квадрата равна 10 см.
Пример 2:
Даны два квадрата. Сторона первого квадрата в два раза больше стороны второго квадрата. Найдите, во сколько раз площадь первого квадрата больше площади второго квадрата.
Решение:
Пусть х – длина стороны второго квадрата. Тогда сторона первого квадрата будет равна 2x. Площадь первого квадрата равна (2x)^2 = 4x^2, а площадь второго квадрата равна х^2. Таким образом, площадь первого квадрата в 4 раза больше площади второго квадрата (4x^2 / х^2 = 4).
Ответ: площадь первого квадрата в 4 раза больше площади второго квадрата.
Пример 3:
Найдите сторону квадрата, зная, что его площадь равна 121 см^2.
Решение:
Используя формулу для площади квадрата, найдем значение стороны:
x^2 = 121
x = 11 см
Ответ: сторона квадрата равна 11 см.
Различные единицы измерения стороны квадрата
В математике сторона квадрата является одной из основных характеристик этой геометрической фигуры. Она определяется как отрезок, соединяющий две противоположные вершины квадрата и одновременно является его стороной. Сторона квадрата является основой для вычисления различных параметров и характеристик этой фигуры.
Стандартной или единичной единицей измерения стороны квадрата является метр. Однако, в различных ситуациях может потребоваться использование других единиц измерения, которые могут отличаться по размерности и назначению.
Одной из наиболее распространенных альтернативных единиц измерения стороны квадрата является сантиметр. Эта единица измерения используется в школьных учебниках и задачах, а также в повседневной жизни для измерения мелких размеров и длин.
Другой альтернативной единицей измерения стороны квадрата может являться фут или дюйм. Эти единицы измерения используются в системе мер США и Великобритании и могут использоваться для вычисления параметров квадрата, если он был измерен в этих единицах измерения.
- Метр
- Сантиметр
- Фут
- Дюйм
При работе с квадратами и их сторонами важно помнить о правильном выборе единицы измерения, чтобы избежать ошибок и получить точные результаты.
Как найти длину диагонали квадрата по его стороне
Диагональ квадрата – это отрезок, соединяющий противоположные вершины. Чтобы найти длину диагонали квадрата по его стороне, можно использовать теорему Пифагора.
Согласно этой теореме, в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов. В случае квадрата, его диагональ является гипотенузой, а стороны – катетами.
Поэтому, чтобы найти длину диагонали квадрата, необходимо возвести длину его стороны в квадрат, умножить на 2 и извлечь из полученного числа корень квадратный:
Длина диагонали квадрата = √2*(длина стороны)
Например, если длина стороны квадрата равна 5 см, то длина его диагонали будет:
√2*5 ≈ 7,07 см






