Углы в математике 5 класс – это различные геометрические фигуры, имеющие свойство измеряться в градусах. В статье вы найдете описание типов углов и их названий, а также иллюстрации для лучшего понимания материала.
Математика в 5 классе является рядом важных предметов, которые позволяют детям развивать абстрактное мышление и общие представления о пространстве.
Один из основных элементов геометрии – это углы. Угол – это область пространства, заключенная между двумя лучами, которые имеют общее начало. Они играют важную роль в жизни людей, особенно в разных областях науки и технологии.
Углы различаются по величине и названиям. В некоторых случаях их форма также играет важную роль. Эта статья расскажет о различных типах углов, которые изучаются в 5-м классе, а также о их названиях и повседневном использовании.
Основные понятия
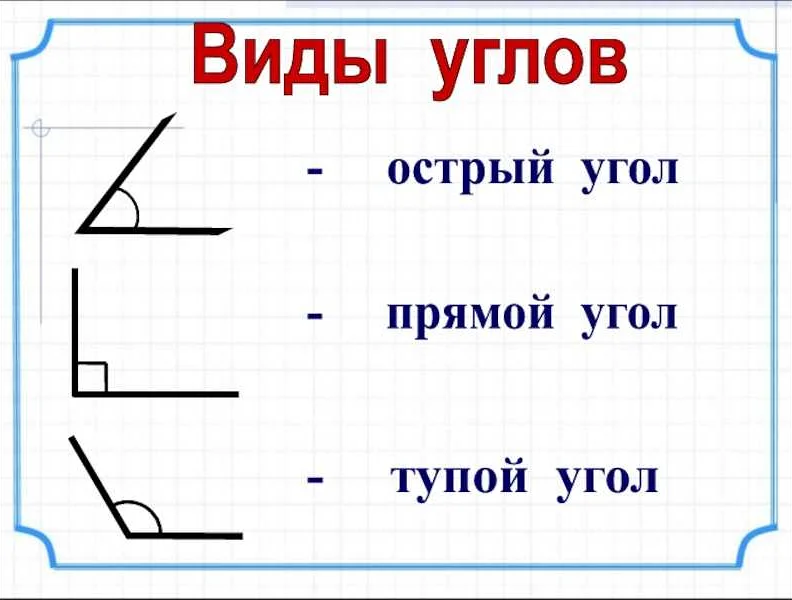
Углы – это геометрические фигуры, которые образуются при пересечении двух лучей. Одна из прямых называется стороной угла, а точка пересечения – вершиной угла.
Прямой угол – это угол, который равен 90 градусам. Он образуется, когда две стороны угла расположены на одной прямой линии.
Острый угол – это угол, который меньше 90 градусов. Он обозначаетсся так: <ABC.
Тупой угол – это угол, который больше 90 градусов. Он обозначается так: <DEF.
Смежные углы – это углы, которые имеют общую сторону. Например, <ABC и <CBD являются смежными углами, потому что у них есть общая сторона <BC.
Вертикальные углы – это пара углов, которые находятся напротив друг друга и имеют общую вершину.
Понимание углов и их свойств является важным базисом в геометрии для всех учащихся.
Прямой угол
Прямой угол – это угол, который равен 90 градусам. Он образуется двумя пересекающимися линиями, которые образуют перпендикуляр. Прямой угол также называется прямым углом или прямым.
Прямой угол может быть обозначен несколькими способами, например, с помощью специального символа, который выглядит как квадрат с вертикальной линией, проходящей через центр. Этот символ обычно ставится в уголке между двумя линиями, образующими прямой угол.
Прямой угол играет важную роль в геометрии и является основой для многих других понятий, таких как острый угол и тупой угол. Он также используется в решении задач по теории вероятности и статистике.
- Как определить, что угол является прямым:
- Проверьте, что две линии, образующие угол, перпендикулярны друг другу.
- Измерьте угол с помощью транспортира. Если он равен 90 градусам, то это прямой угол.
- Как использовать прямой угол в задачах:
- Определить, будет ли треугольник прямоугольным, если известны два угла и их сумма равна 90 градусов.
- Найти противоположный угол в прямоугольном треугольнике, используя теорему Пифагора.
Таким образом, знание понятия прямого угла является необходимым для решения задач в геометрии и других областях математики.
Наружный угол
Наружный угол – это угол, который образуется между продолжением одного из сторон многоугольника и продолжением соседней стороны. Внешний угол может быть острый, тупой или прямой, в зависимости от угла, который он образует с продолжением соседней стороны.
Если в многоугольнике есть n углов, то число внешних углов также будет равно n. Так, в четырехугольнике будет 4 внешних угла. Внешний угол и соответствующий ему внутренний угол многоугольника в сумме дают 180 градусов.
Наружные углы часто используются в решении задач геометрии, связанных с многоугольниками. Например, поиск суммы всех внешних углов многоугольника, нахождение значения одного из внешних углов по известным данным о других углах многоугольника и т.д.
- Примеры многоугольников с наружными углами:
- Треугольник
- Четырехугольник
- Пятиугольник
- Шестиугольник
Важно помнить, что наружный угол не должен путаться с углом между продолжением одной стороны многоугольника и перпендикуляром к соседней стороне, который называется острым углом. Это два разных понятия геометрии.
Внутренний угол
Внутренний угол – это угол, который расположен между двумя сторонами фигуры и направлен внутрь ее контура. Внутренние углы могут быть остроугольными, прямоугольными и тупоугольными. Сумма внутренних углов в любой многоугольной фигуре равна (n-2)·180 градусов, где n – количество сторон фигуры.
Остроугольный внутренний угол имеет значение менее 90 градусов, прямоугольный внутренний угол равен 90 градусам, а тупоугольный внутренний угол больше 90 градусов.
Для нахождения величины внутреннего угла можно использовать различные формулы в зависимости от типа фигуры и известных параметров. Например, для треугольника можно воспользоваться формулой синусов или косинусов, а для квадрата – просто разделить 360 градусов на количество углов.
Знание типов внутренних углов и способов их нахождения является основой геометрии и необходимо для решения различных задач, связанных с определением площади и периметра фигур, построением графиков и диаграмм, а также в инженерных расчетах и других областях знаний.
Острый угол
Острый угол – это такой угол, который меньше 90 градусов. Его можно представить себе как острый уголный конус или острый уголный треугольник.
Острый угол в математике является одним из основных типов углов, о которых учатся в 5 классе. Он может быть измерен различными способами, например, градусами, радианами или градусными минутами.
Острый угол может быть применен в различных областях математики, таких как геометрия, тригонометрия и алгебра. Например, при решении задач на нахождение площади треугольника или нахождение длины стороны правильного многоугольника, может быть использован острый угол.
Острый угол также используется в решении задач на работу с пропорциями, а также может быть использован при расчете вероятности событий. Он является важным элементом математических рассуждений и может быть полезным во многих областях жизни, где требуется точность и вычислительная мощность.
Тупой угол
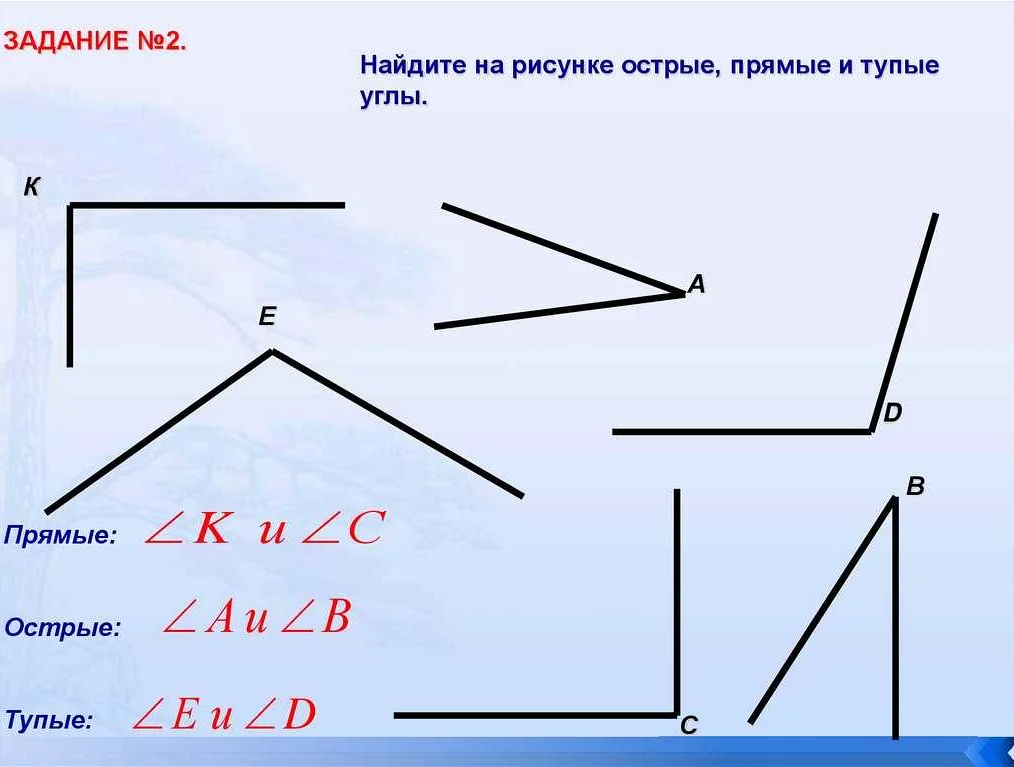
Тупой угол — это угол, который больше 90 градусов и меньше 180 градусов.
На картинке тупой угол изображен как угол, который является раскрытием от угла прямого.
Тупой угол можно встретить в различных задачах геометрии, например, при изучении треугольников или многоугольников.
Для геометрических построений с тупым углом можно использовать соответствующие инструменты и формулы, чтобы вычислить его размеры и свойства.
Важно помнить, что тупой угол не является особенным или страшным, он просто один из многих видов углов в математике.
Разнообразие видов углов в природе и технике
Углы являются фундаментальным понятием в геометрии. Они возникают не только в математике, но и во многих других областях. Например, в природе мы можем наблюдать углы между листами деревьев или между ветвями, которые растут в разных направлениях. Кроме того, углы можно увидеть в льдах, округленных и острых камнях или в различных формах облаков на небе.
В технике углы также играют важную роль. Например, при проектировании зданий и мостов используются различные типы углов, такие как острые углы, прямые углы и тупые углы. Эти углы помогают инженерам и архитекторам строить крепкие и надежные сооружения. Некоторые углы также используются в производстве, например, в чертежах и конструкциях.
Существует множество различных типов углов, каждый из которых имеет свои особенности. Это острые углы, прямые углы, тупые углы и многие другие. Некоторые углы могут быть повернуты на 360 градусов, как например в случае с круговым углом. Другие углы могут быть симметричными или пересекающимися.
- Прямой угол – имеет меру 90 градусов и выглядит как прямая линия, пересекающая другую прямую линию.
- Тупой угол – имеет меру больше 90 градусов, например, в угле между двумя стенами в углу комнаты.
- Острый угол – имеет меру меньше 90 градусов, например, в углу между двумя стрелками часов.
Важно понимать, что углы могут быть разными, но каждый тип угла важен и необходим в геометрии, природе и технических науках.
Измерение углов
Угол – это геометрическая фигура, образованная двумя лучами, выходящими из одной точки, называемой вершиной. Измерение углов необходимо в различных областях математики, физики, географии, инженерии и др.
Углы могут быть различных видов: прямыми, острыми, тупыми, ровными, смежными и противолежащими. Один из основных способов измерения углов – это использование градусной меры.
Градус – это одна из единиц измерения углов. Полный угол составляет 360 градусов. Прямой угол равен 90 градусам, острый – меньше 90 градусов, тупой – больше 90 градусов.
Для измерения углов существует также радианная мера. Радиан – это угол, величина которого соответствует длине дуги на окружности, равной радиусу. Полной окружности соответствует 2π радиан.
Измерение углов используется для решения задач как в плоской геометрии, так и в пространственной геометрии. Например, при вычислении площади треугольника, при определении координат точки на плоскости, при рассчете угла наклона подъема дороги или же при проектировании зданий и сооружений.
Особенности задач на углы
Задачи на углы в математике 5 класса – это одна из самых интересных тем, которую изучают ребята. В процессе решения задач на углы, ученики узнают о разных типах углов и их свойствах.
Одной из особенностей задач на углы является то, что они могут быть как простые, так и сложные. Некоторые задачи требуют глубокого понимания углов и их свойств, в то время как другие могут быть решены за несколько минут.
Для того, чтобы эффективно решать задачи на углы, важно понимать основные типы углов: прямой угол, тупой угол, острый угол и т.д. Кроме того, нужно знать свойства углов, например, то, что угол вписанный в окружность равен половине центрального угла, опирающегося на ту же дугу.
Важно помнить, что при решении задач на углы нужно использовать логику и смекалку. Многие задачи на углы требуют аналитического мышления и умения работать с формулами.
В итоге, решая задачи на углы, ученики улучшают свои навыки в математике и развивают логическое мышление, что будет полезно в дальнейшем обучении.
Изучение углов в школьной программе
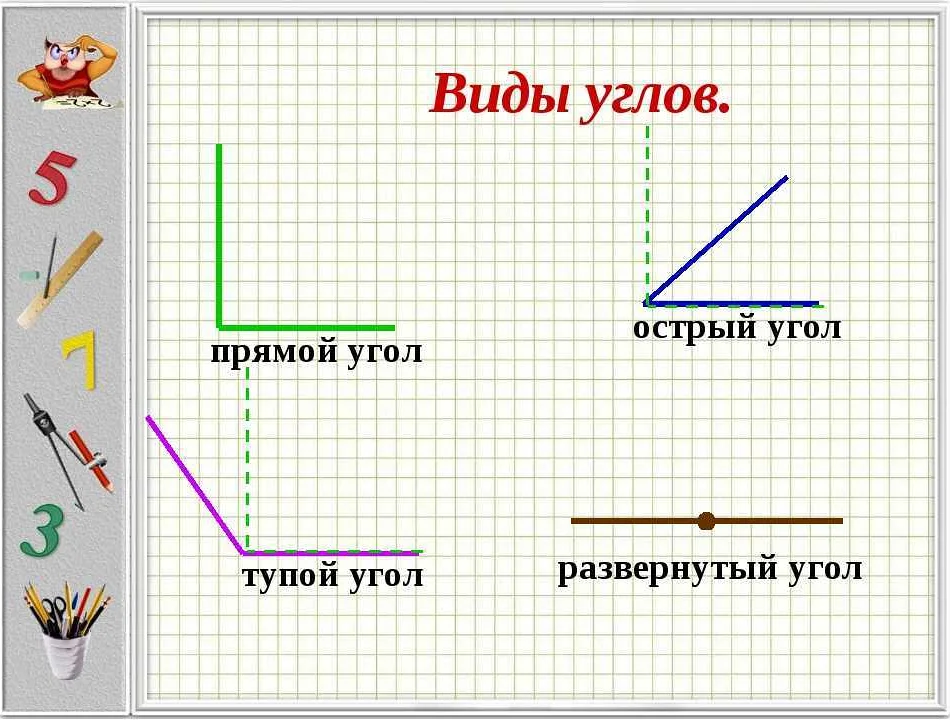
Изучение углов является важным компонентом школьной математической программы. Углы служат основой для изучения геометрических фигур и их свойств, а также играют важную роль в решении задач.
В начальных классах учатся углы прямые, острые и тупые. Ученики проводят опыты с гончарным кругом и измеряют углы с помощью геометрических инструментов. В 5 классе изучают углы, составляющие прямую, а также смежные и вертикальные углы. Ученики учатся рассчитывать значения углов и строить углы по заданным параметрам.
Углы также изучаются в других предметах, таких как физика, геометрия и черчение. Знание углов и их свойств позволяет ученикам лучше понимать пространственные отношения и использовать их в повседневной жизни.
В целом, изучение углов является неотъемлемой частью школьной программы, и его понимание будет полезно в будущих учебных предметах и профессиях.
Практическое применение знаний об углах
Знание углов и их свойств имеет реальное применение в жизни. Например, инженеры и архитекторы используют знания об углах для построения зданий и сооружений.
Также знание углов важно для автолюбителей – правильный угол поворота колеса в автомобиле может улучшить управляемость и безопасность на дороге. В авиации углы используются для расчета траектории полета и поворотов.
В кулинарии знание углов поможет правильно нарезать продукты и приготовить блюда в форме треугольников, полукругов и кругов.
Для любителей фотографии важно знать углы, чтобы выбрать наиболее выгодный ракурс снимка. Также знания об углах помогают в коммуникациях и дискуссиях, где нужно точно определить направление и отношение объектов друг к другу.
В общем, знание углов и их свойств на практике позволяет нам эффективно пользоваться разнообразными предметами и пространством вокруг нас, а также глубже понимать окружающий мир.
Вопрос-ответ:
Какие бывают углы?
В математике углы бывают различных типов: прямой, острый, тупой, двугранный, трехгранный, поворотный и др.
Что такое прямой угол?
Прямой угол — это угол, равный 90°. Такой угол можно наблюдать, например, при стыковке двух перпендикулярных линий.
Как называется угол меньше 90 градусов?
Угол, меньший 90°, называется острым. Такой угол обычно имеет острый конец.
Что такое двугранный угол?
Двугранный угол — это угол, образованный двумя пересекающимися лучами. В зависимости от угла между лучами он может быть острым, прямым или тупым.
Что такое поворотный угол?
Поворотный угол — это угол, который образуется при повороте одной прямой относительно другой прямой. Угол может быть как положительным, так и отрицательным.
Что такое трехгранный угол?
Трехгранный угол — это угол, образованный тремя плоскостями. Такой угол можно наблюдать, например, при пересечении трех плоскостей.
Какие еще бывают углы в математике?
В математике существуют и другие типы углов, например, биссектриса угла, вписанный угол, центральный угол, альтернативный угол и др. Но они не столь основательны, как прямой, острый и тупой углы.






