Круглая скобка в математике — это символ, который используется для обозначения группировки выражений. Она помогает приоритизировать операции и правильно вычислять выражения. Без использования скобок, результат может быть неверным. Узнайте больше о круглой скобке в математике в нашей статье.
Круглая скобка – один из наиболее распространенных математических символов. Она используется во многих областях математики, включая алгебру, анализ, геометрию и теорию вероятности. Круглые скобки выражают группировку математических выражений, указывая на порядок выполнения операций. Они могут также использоваться для обозначения диапазона значений или декартового произведения чисел.
Круглая скобка играет важную роль в составлении математических формул и выражений. Она позволяет упростить вычисления, улучшить читабельность и избежать ошибок. В некоторых случаях круглые скобки являются обязательными, чтобы установить определенные правила приоритета выражений.
Например, выражение 2 + 3 * 4 может быть проинтерпретировано по-разному без круглых скобок. Если необходимо выполнить сложение сначала, следует написать (2 + 3) * 4, чтобы получить результат 20. Если же нужно выполнить умножение сначала, можно написать 2 + (3 * 4), чтобы получить результат 14.
Общие сведения
Круглая скобка в математике используется для определения порядка выполнения действий в выражениях.
Например, в выражении 3 + 4 × 2 без скобок нужно сначала умножить 4 × 2, а затем прибавить 3, получится 11. Однако, если поставить скобки: 3 + (4 × 2), то сначала выполнится умножение 4 × 2, а затем прибавление 3, получится 11.
Круглые скобки также используются для определения дробей. Например, выражение 1/(2 + 3) означает дробь, в числителе которой 1, а в знаменателе результат выполнения выражения 2 + 3.
Кроме того, круглые скобки могут использоваться для обозначения аргументов функций. Например, функция sin(x) означает синус угла x.
Использование круглых скобок в математике важно, потому что без них результат выполнения выражения может быть неправильным. Приоритет выполнения действий определяется именно по наличию скобок.
Основы арифметики
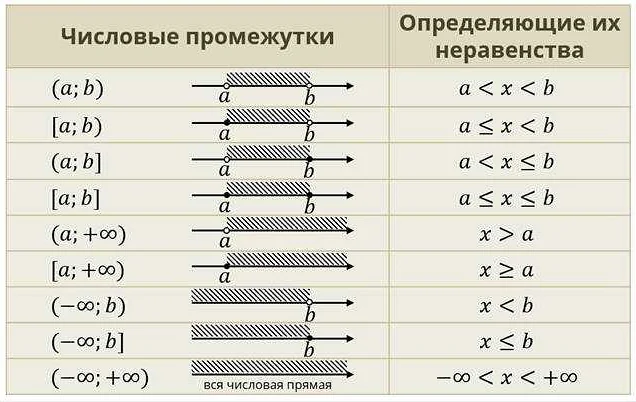
Арифметика — это раздел математики, который изучает свойства и операции с числами. Основными операциями в арифметике являются сложение, вычитание, умножение и деление. С их помощью мы можем решать задачи, производить измерения и проводить анализ данных.
Сложение — это операция, которая позволяет нам объединять два или более числа в одно. Результатом сложения является сумма чисел.
Вычитание — это операция, которая позволяет нам находить разность между двумя числами. Результатом вычитания является разность чисел.
Умножение — это операция, которая позволяет нам находить произведение двух чисел. Результатом умножения является произведение чисел.
Деление — это операция, которая позволяет нам находить частное двух чисел. Результатом деления является частное чисел.
Также для работы с числами в арифметике широко используются круглые скобки. Они используются для определения порядка выполнения арифметических операций.
- Первым выполнится операция, находящаяся в круглых скобках
- Затем будут выполнены операции умножения и деления в том же порядке, в котором они записаны
- В конце выполнится сложение и вычитание в том же порядке, в котором они записаны
Алгебраические выражения
Алгебраическое выражение представляет собой математическую комбинацию чисел, переменных и арифметических операций. Круглые скобки в алгебраических выражениях используются для определения порядка выполнения операций (приоритетов). Запись выражений в скобках значительно упрощает понимание порядка выполнения арифметических действий.
Алгебраические выражения могут содержать переменные, которые необходимо подставить вместо буквенных обозначений, чтобы вычислить значение выражения. Например, (5+a)*4 – b является алгебраическим выражением, где a и b – переменные, а 5 и 4 – числа, а звездочка (*) – знак умножения.
Круглые скобки могут использоваться не только для определения порядка выполнения операций, но и для группировки слагаемых в алгебраических выражениях с несколькими переменными. Например, (4x + 3y) – (2x – y) = 2x + 4y.
- Операции над алгебраическими выражениями (сложение, вычитание, умножение, деление и возведение в степень) должны проводиться в правильном порядке, учитывая приоритет операций и скобки.
- Алгебраические выражения могут быть упрощены путем сокращения одинаковых слагаемых, выноса общих множителей за скобки и т.д.
В алгебре круглые скобки часто используются для универсального обозначения функций, например, функций суммирования и умножения. Например, суммирование от 1 до 100 можно записать как:
∑(i=1 to 100) i = 1 + 2 + 3 + … + 100
Здесь ∑(i=1 to 100) – это обозначение суммы, и i – переменная суммирования, которая принимает значения от 1 до 100.
Функции и их графики
Функция – это математический объект, который проецирует элементы одного множества на элементы другого множества. Функции часто описываются в виде формулы, например, y = x^2 + 2x – 3. В этом случае функция связывает каждое значение координаты x с соответствующим значением координаты y.
График функции – это взаимное отображение множеств, которые связывают функцию. Если функция задана в виде формулы, то ее график – это множество точек на координатной плоскости, которые определяются путем подстановки всех возможных значений x в выражение для y.
График функции может помочь понять, как функция работает и как она связывает между собой значения x и y. Например, график функции y = x^2 + 2x – 3 имеет форму параболы ветвями вверх. Он помогает понять, что значение y возрастает при повышении значения x.
График функции может быть представлен как в виде картины на бумаге, так и в виде числовой таблицы, в которой заданные значения x и соответствующие значения y расположены в двух столбцах. В этом случае таблица может быть очень полезной, если требуется найти значения функции в точках, которые не заключены в рассматриваемом интервале.
Кроме того, график функции может быть представлен в виде численной таблицы значений, в которой указаны значения координат x и y в определенных точках. Такие таблицы могут помочь лучше понять свойства функции и ее график, особенно если требуется вычислить значение функции в точках, которые не входят в интервал, в котором график функции задан формулой.
Дроби и проценты
Дроби – это числа, которые показывают, сколько частей целого составляет данное число. Дроби представляются в виде дробной линии, в которой числитель находится над знаменателем и разделены чертой. Например, дробь 2/3 означает, что целое число разделено на три равные части и взято две из них.
В математике дроби могут быть использованы для выражения процентов. Например, если имеется дробь 3/4, то это означает, что целое число разделено на четыре равные части и взяты три. Это может быть переведено в проценты путем умножения на 100 и деления на знаменатель. Так, дробь 3/4 представляет 75%.
Проценты – это отношение одной величины к 100. Они используются для измерения доли чего-либо в процентах от общего числа. Например, если из 100 яблок 75 – зеленые, то можно сказать, что доля зеленых яблок составляет 75% от общего числа яблок. Проценты могут быть выражены в дробном виде и наоборот, дроби – в процентах.
Для преобразования дробей в проценты необходимо умножить дробь на 100 и разделить на знаменатель. Например, если имеется дробь 4/5, то можно преобразовать ее в проценты, умножив на 100 и делением на 5: 4 / 5 * 100% = 80%.
Заключение – дроби и проценты широко используются в математике и имеют различные применения. Понимание этих концепций может быть полезно для решения задач и выполнения различных математических операций.
Геометрия и тригонометрия
Круглая скобка широко используется в геометрии и тригонометрии, чтобы обозначить углы и координаты точек на плоскости. Она используется в определении координат точек в декартовой системе координат, где x-координата обозначается первым числом в скобках, а y-координата – вторым числом в скобках: (x, y). Это позволяет нам точно представлять и измерять положение объектов на плоскости.
Круглая скобка также используется для обозначения углов в тригонометрии. Тригонометрические функции, такие как синус, косинус и тангенс, зависят от угла, который определяется числом в круглых скобках, расположенном после функции. Например, sin(45°) обозначает синус угла в 45 градусов.
Геометрия и тригонометрия являются важными областями математики, применяемыми в различных науках и технологиях. Они помогают изучать формы и размеры объектов в пространстве, а также понимать соотношения между различными тригонометрическими функциями. Использование круглой скобки в этих областях помогает создавать точные математические модели и решать задачи, связанные с геометрией и тригонометрией.
Математические операции
Математические операции – это действия, которые выполняются с числами или другими математическими объектами. Основные операции, которые мы изучаем в математике – это сложение, вычитание, умножение и деление.
Сложение – это операция, которая позволяет нам находить сумму двух или более чисел. Например, сумма чисел 2 и 3 равна 5.
Вычитание – это операция, которая позволяет нам находить разность между двумя числами. Например, разность между числами 5 и 3 равна 2.
Умножение – это операция, которая позволяет нам находить произведение двух или более чисел. Например, произведение чисел 2 и 3 равно 6.
Деление – это операция, которая позволяет нам находить частное между двумя числами. Например, частное от деления числа 6 на число 3 равно 2.
На ряду со стандартными математическими операциями, существуют и другие математические операции, такие как возведение в степень, извлечение корня и т.д. Каждая из них имеет свои особенности и правила использования.
Знание математических операций и умение правильно выполнять их – это важные навыки, которые помогут не только в школе, но и в повседневной жизни.
Формулы и уравнения
Формула – это математическое выражение, записанные с помощью символов и знаков операций. Формулы используются для описания законов природы и решения задач в различных областях, включая физику, химию, экономику и другие науки.
Уравнение – это математическое равенство, содержащее переменные и знак равенства. Оно описывает отношения между переменными и используется для решения задач и нахождения неизвестных значений.
Примеры формул:
- Формула Пифагора: $a^2+b^2=c^2$
- Закон Кулона: $F = k\frac{q_1q_2}{r^2}$
Примеры уравнений:
- Линейное уравнение: $ax+b=0$
- Квадратное уравнение: $ax^2+bx+c=0$
Знаки операцийЗнакОписаниеПример
| + | сложение | $3+5=8$ |
| – | вычитание | $7-2=5$ |
| * | умножение | $2*4=8$ |
| / | деление | $10/2=5$ |
Ряды и последовательности
Ряд – это сумма бесконечного числа слагаемых, которые могут быть числами или функциями. Если ряд сходится, то его сумму можно вычислить. Если ряд расходится, то его сумму невозможно вычислить.
Последовательность – это упорядоченный набор чисел. Последовательность можно задать формулой, например, n-ый член последовательности a может быть определен как an = n2 + 1. Последовательность может быть ограничена сверху или снизу, то есть имеет максимальный или минимальный элемент. Также последовательность может сходиться к какому-то конечному пределу или расходиться и не иметь предела.
Для изучения рядов и последовательностей в математике используются специальные методы, такие как тесты сходимости для рядов или определение предела последовательности. Кроме того, ряды и последовательности имеют множество приложений в других областях математики, физики, экономики и т. д.
- Примеры рядов: геометрическая прогрессия, гармонический ряд, ряд Тейлора.
- Примеры последовательностей: последовательность фибоначчи, последовательность простых чисел, последовательность синуса.
Изучение рядов и последовательностей требует серьезных знаний математики и опыта работы с числами и функциями. Как и в любой области математики, важно практиковаться и решать множество задач для понимания основных концепций и методов.
Теория вероятности и математическая статистика
Теория вероятности и математическая статистика – это отрасль математики, которая занимается изучением случайных явлений и разработкой методов для их описания и предсказания.
Теория вероятности и математическая статистика нашла применение во многих областях, включая физику, экономику, медицину, технику, социологию и многие другие.
В теории вероятности изучаются математические модели случайных явлений, такие как игры, бросание костей, вероятности наступления различных событий и т.д. Математическая статистика же позволяет сделать выводы на основе данных, полученных в результате экспериментов или исследований.
Например, если мы хотим определить, какую долю голосов получит определенный кандидат на выборах, мы можем провести опрос и используя теорию вероятности и математическую статистику вычислить с какой вероятностью результаты опроса точно отражают мнение всего населения.
Таким образом, теория вероятности и математическая статистика являются необходимой частью современной науки и позволяют нам более точно понимать и предсказывать мир вокруг нас.
Вопрос-ответ:
Для чего используют круглые скобки в математике?
Круглые скобки используются в математике для ограничения порядка выполнения арифметических действий, для выделения подынтервала в записи интервала и для указания аргумента при вызове функции. Также их можно использовать для лучшего читаемости формул и выражений.
Какие арифметические операции можно выполнять внутри круглых скобок?
Внутри круглых скобок можно выполнять все арифметические операции, в том числе умножение, деление, сложение, вычитание и возведение в степень. При этом порядок выполнения операций определяется приоритетом операций, который указывается с помощью скобок разных типов (круглых, квадратных и фигурных).
Как можно использовать круглые скобки при решении уравнений?
При решении уравнений круглые скобки могут использоваться для сокращения или раскрытия выражений, а также для изменения порядка выполнения арифметических действий. Например, при решении уравнения 3(2x-1) = 12 можно раскрыть скобки и получить 6x-3 = 12, а затем решить его методом преобразования уравнений к более простому виду.
Можно ли использовать круглые скобки без чисел и букв?
Да, можно использовать круглые скобки без чисел и букв для выделения какого-либо элемента в тексте, например чтобы обозначить примечание или уточнение. Однако при использовании скобок в тексте нужно убедиться, что они не вызывают недопонимания.
Как круглые скобки связаны с функциями в математике?
Круглые скобки используются в математике для указания аргумента при вызове функции. Например, функция синуса можно записать как sin(x), где x – аргумент функции, который может быть любым числом или выражением. Круглые скобки также могут использоваться для группировки аргументов функции.
Как круглые скобки используются при операциях с матрицами?
Круглые скобки обычно используются для выделения элементов матрицы. Например, матрицу A можно записать следующим образом: A = (a11 a12 … a1n; a21 a22 … a2n; …; am1 am2 … amn), где aij – элемент матрицы A. Внутри круглых скобок элементы матрицы разделяются запятой, а строки матрицы разделяются точкой с запятой.
Как круглые скобки используются в теории вероятности?
В теории вероятности круглые скобки обычно используются для группировки элементов, на которых выполняется арифметическая операция. Например, вероятность суммы двух событий можно записать как P(A+B), где A и B – события, а + обозначает логическое ИЛИ. Круглые скобки также могут использоваться для указания условий событий.
Применение круглых скобок в различных областях
Математика: Круглые скобки используются для группировки в формулах и выражениях. Они помогают определить порядок выполнения действий и ускоряют вычисления. Также круглые скобки используются для обозначения координат.
Лингвистика: Круглые скобки используются для обозначения дополнительной информации, которая не является обязательной. Например, для обозначения произношения слов, для приведения разъяснений или дополнительных пояснений к тексту.
Программирование: Круглые скобки используются для определения параметров функций и методов. Они также могут использоваться для группировки операторов в условных и циклических конструкциях.
Физика: Круглые скобки используются для обозначения размерности физических величин в системе СИ. Например, масса обозначается в килограммах (кг), а размерность момента силы в ньютон-метрах (Н·м).
Другие области: Круглые скобки могут использоваться в различных областях, таких как музыка, юриспруденция, экономика и др. Например, в музыке круглые скобки используются для обозначения аккордов, а в юриспруденции – для обозначения дат и сроков.






