Звенья в математике у ломаной – это точки пересечения ломаной с осью координат. Они помогают определить значение функций в различных точках и являются важным элементом графического анализа функций. Узнайте больше о звеньях в математике на нашем сайте.
Ломаная линия в математике представляет собой график функции, заданной на отрезке. В процессе построения ломаной, график функции на этом отрезке будет состоять из отрезков прямых линий, соединенных в точках пересечения, которые называются звеньями.
Каждое звено ломаной является отрезком прямой между двумя точками на графике функции. Количество звеньев ломаной соответствует количеству узлов (точек пересечения). Один из способов отображения ломаной в математике – это графическое представление, когда звенья ломаной рисуются в виде отрезков прямых линий, соединенных точками пересечения.
Звенья ломаной главным образом используются для анализа функций, построения графиков и решения задач геометрии. Они важны с точки зрения анализа определенных свойств функции, таких как монотонность, экстремумы и выпуклость/вогнутость графика.
Звенья в математике у ломаной
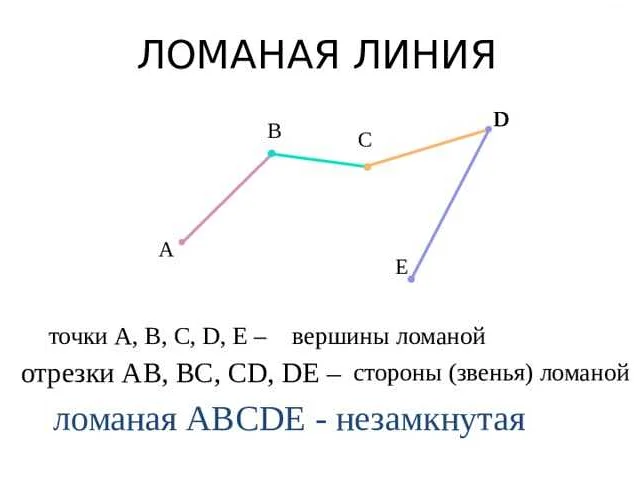
Ломаная – это геометрическая фигура, представляющая собой набор отрезков, соединяющих точки на плоскости. Звеном ломаной называют отрезок, соединяющий две соседние точки этой фигуры.
Количество звеньев в ломаной зависит от количества точек, из которых она состоит. Например, если ломаная проходит через пять точек, то количество звеньев будет на единицу меньше – четыре.
Звенья ломаной имеют важное значение в математике, так как определяют ее форму и свойства. Например, при аппроксимации ломаной функцией производится разбиение ее на части, каждая из которых задается своей функцией. Формула длины ломаной также заключается в сумме длин ее звеньев.
Звенья ломаной могут также использоваться для построения графиков. Каждое звено соответствует значению функции в определенной точке. Если последовательно соединить звенья, то получится график функции, заданной ломаной.
- Выводы:
Таким образом, звенья ломаной важны для определения ее формы и свойств, используются в аппроксимации функций и построении графиков.
Определение звеньев в математике
Звено в математике – это отрезок, соединяющий две точки на ломаной. В ломаной, у которой есть хотя бы две звенья, каждое звено определяется двумя точками: начальной и конечной.
В математических задачах и графиках звенья могут быть выделены цветом, обозначены буквами или цифрами, чтобы проще оперировать ими при вычислениях и анализе данных.
Звено является важным элементом ломаной, так как устанавливает форму и расстояние между точками, и влияет на её свойства и особенности. Например, длина всех звеньев одинакова говорит о том, что ломаная является равнобедренной.
В графическом представлении звено может быть представлено в виде отрезка прямой, дуги окружности, спирали, параболы и т.д., в зависимости от задачи и контекста.
Таким образом, звено является важным понятием в математике и играет важную роль в различных областях, таких как геометрия, статистика, физика, экономика и другие.
Как вычислить количество звеньев ломаной
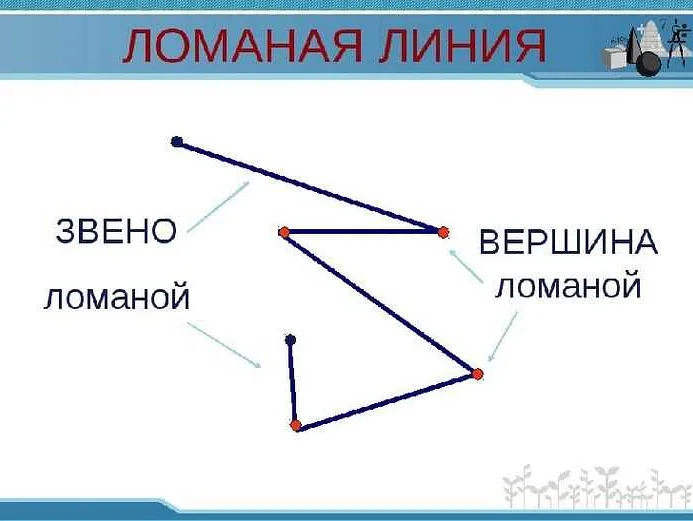
Звено ломаной – это отрезок между двумя точками, в которых она меняет направление. Количество звеньев ломаной – это количество таких отрезков, но на один меньше, чем количество вершин ломаной.
Чтобы вычислить количество звеньев ломаной, нужно посчитать количество вершин. Вершина ломаной – это точка, в которой она меняет направление. Если у нас есть координаты точек ломаной, то вершиной считается точка, в которой значение одной из координат меняется.
Проще всего подсчитать количество звеньев ломаной, нарисовав ее на бумаге и визуально определив количество вершин. В случае, если координаты точек ломаной представлены в таблице, можно пройти по ней и посмотреть, сколько раз меняется значение одной из координат. Это будет и являться количеством звеньев ломаной.
Примеры ломаных с разным количеством звеньев
Ломаная с двумя звеньями:
Примером ломаной с двумя звеньями может служить отрезок прямой, который разбивается на две части любой формы. Например, отрезок, соединяющий две точки.
Ломаная с тремя звеньями:
Примером ломаной с тремя звеньями может служить треугольник. При соединении трех точек на плоскости, мы получаем треугольную ломаную.
Ломаная с четырьмя звеньями:
Примером ломаной с четырьмя звеньями может служить многоугольник. Многоугольник – это фигура, у которой более трех сторон. При соединении вершин многоугольника, мы получаем ломаную с четырьмя звеньями.
Ломаная с пятью звеньями:
Примером ломаной с пятью звеньями может служить пятиугольник. Пятиугольник – это многоугольник с пятью сторонами. При соединении всех его вершин, мы получаем ломаную с пятью звеньями.
Ломаная с шестью звеньями:
Примером ломаной с шестью звеньями может служить шестиугольник. Шестиугольник – это многоугольник с шестью сторонами. При соединении вершин шестиугольника, мы получаем ломаную с шестью звеньями.
Графическое представление звеньев ломаной на координатной плоскости
Звенья ломаной могут быть графически представлены на координатной плоскости. Для этого необходимо знать координаты точек, через которые проходит ломаная.
Если известны координаты точек, то можно построить график ломаной на координатной плоскости. Для этого нужно соединить все точки отрезками прямых линий в порядке, который определяется порядком следования точек.
Можно использовать специальную программу для построения графиков, например, Microsoft Excel или GeoGebra. В программе необходимо указать координаты точек и построить график.
Также можно использовать таблицу со списком координат точек и ручку с линейкой для рисования ломаной на бумаге. В этом случае линии будут не такие точные, как на компьютере, но это не должно сильно повлиять на результат.
Графическое представление звеньев ломаной на координатной плоскости помогает визуализировать и анализировать форму и направление ломаной. Это может быть полезно в различных приложениях, например, при построении графиков функций или карт на картах.
Как использовать звенья при решении задач на геометрию
Звенья в математике – это отрезки на ломаной. Они могут быть горизонтальными или вертикальными, наклонными или диагональными. Звенья могут служить мощным инструментом при решении задач на геометрию, особенно если используются вместе с другими инструментами геометрии, например, с углами и расстояниями.
Использование звеньев в качестве опорных точек: одним из способов использования звеньев при решении задач на геометрию является использование их в качестве опорных точек. Например, если нужно построить перпендикуляр к отрезку, можно использовать звено на его конце в качестве опорной точки для построения перпендикуляра.
Использование звеньев для измерения расстояний: звенья могут также использоваться для измерения расстояний. Например, если нужно найти расстояние между двумя точками, можно использовать звено и перемещать его от одной точки до другой, затем измерить длину звена.
Использование звеньев для вычисления углов: звенья могут помочь в вычислении углов. Например, если нужно найти угол между двумя отрезками, можно использовать звено, чтобы соединить концы отрезков и измерить угол, который образуется.
Использование звеньев для построения фигур: Еще один способ использования звеньев – это построение фигур. Можно использовать звенья для построения периметра фигуры и затем измерить длину периметра с помощью звенья
Использование звеньев в геометрии может быть очень эффективным и помочь в решении различных задач. Главный секрет – в том, чтобы использовать звенья вместе с другими инструментами геометрии и помнить о том, что они могут служить для разных целей.
Взаимосвязь звеньев и углов при ломаной
Ломаная является геометрической фигурой, состоящей из звеньев, которые соединены между собой. При этом между каждыми двумя смежными звеньями образуется угол.
Взаимосвязь между звеньями и углами при ломаной заключается в том, что их количество определяется одним и тем же параметром. То есть, если мы знаем количество звеньев, то мы также знаем количество углов в ломаной и наоборот.
Кроме того, углы могут быть различных типов. Например, углы могут быть прямыми, острыми или тупыми, в зависимости от их величины. Также, углы могут быть равными или неравными друг другу. Все эти параметры могут использоваться при решении задач на ломаные.
Важно также отметить, что звенья могут быть различной длины. Изменение длины звеньев может привести к изменению углов в ломаной. В этом случае, для определения параметров ломаной может быть использовано множество геометрических методов и формул.
Итак, взаимосвязь между звеньями и углами при ломаной выражается в том, что их количество определяется одним и тем же параметром. Углы при ломаной могут быть различных типов и могут зависеть от длины звеньев. Знание этих параметров может быть полезно в решении задач на ломаные.
Метод проекций и его применение при вычислении длины ломаной
Метод проекций является одним из способов нахождения длины ломаной на плоскости. Он основан на проекции каждого звена ломаной на координатные оси и вычислении длины каждой проекции.
Для применения метода проекций необходимо знать координаты всех точек ломаной на плоскости. Далее проводятся проекции каждого звена ломаной на ось x и на ось y, находятся их длины и складываются. Таким образом, получается длина всей ломаной.
Преимущество метода проекций заключается в его простоте и универсальности. Этот метод может быть применен для вычисления длины любой ломаной на плоскости, независимо от ее формы и количества звеньев.
Также метод проекций может быть использован для вычисления других характеристик ломаной, например, ее площади или высоты.
Теорема о параболе и ее связь с количеством звеньев ломаной
Теорема о параболе утверждает, что точка, двигаясь на параболе под действием постоянной скорости, равномерно меняющей направление, проходит за равные промежутки времени равные отрезки пути. Эта теорема была открыта в 1646 году Ферма, а в 1660 году ее вывел производную формулировку Гюйгенс.
Связь теоремы о параболе с количеством звеньев ломаной заключается в том, что при переходе от непрерывной кусочно-линейной функции к ломаной, с увеличением количества звеньев, точность аппроксимации функции увеличивается. Также при помощи ломаных можно точно приблизить параболу, количество звеньев которой будет определять точность.
Кроме того, теорема о параболе используется в теории оптимального управления для определения траектории движения объектов и построения оптимальных управляющих воздействий на эти объекты.
Итак, теорема о параболе и ее связь с количеством звеньев ломаной позволяют более точно приближать кривые и определять траектории движения объектов в теории оптимального управления.
Видео по теме:
Вопрос-ответ:
Зачем использовать звенья в математике при построении ломаных?
Звенья необходимы, чтобы определить конкретные точки на ломаной и зафиксировать ее форму.
Как определить количество звеньев для построения ломаной?
Количество звеньев зависит от количества точек, которые необходимо зафиксировать на ломаной. Обычно для задачи достаточно использовать 2-3 звена.
Можно ли построить ломаную без использования звеньев?
Нет, без звеньев невозможно зафиксировать точки ломаной и ее форму.
Как вычислить длину звена на ломаной?
Длину звена можно найти по формуле: d = √((x2-x1)² + (y2-y1)²), где (x1; y1) и (x2; y2) – координаты точек, между которыми проходит звено.
Какие еще способы можно использовать для построения ломаной кроме звеньев?
Кроме звеньев, можно использовать например, Безье-кривые или Кривые Эрмита.
Какие применения имеют ломаные с звеньями?
Ломаные с звеньями используются при создании графиков, визуализации трехмерных объектов, анимации и в других областях, где необходимо задать точки и изгибы кривой.
Как влияет количество звеньев на форму ломаной?
Чем больше звеньев, тем более плавным будет контур ломаной и тем меньше будут видны углы и изгибы на графике. Меньшее количество звеньев приведет к более заметным углам на кривой.
Как изменится число звеньев ломаной при ее повороте или отражении
Поворот: При повороте ломаной на угол α вокруг центра поворота, число звеньев останется неизменным. Это происходит потому, что поворот не изменяет расстояние между точками, поэтому и количество звеньев остается неизменным.
Отражение: При отражении ломаной относительно оси симметрии, число звеньев также сохранится. Если ось симметрии проходит через одну из вершин ломаной, то звено в этой вершине останется на месте, а все остальные звенья отразятся и изменят свое положение, но количество звеньев не изменится. Если ось симметрии проходит между двумя вершинами, то звенья ломаной отразятся относительно этой оси, но количество звеньев все равно останется неизменным.
Таким образом, при повороте или отражении ломаной ее форма изменится, но количество звеньев останется неизменным. Это свойство используется при решении задач на геометрию, когда требуется найти количество звеньев ломаной в различных ее положениях.
Задачи для самостоятельного решения по теме звенья ломаной
Задача 1: Дана ломаная, состоящая из 4 звеньев. Длина первого звена равна 3 единицам, второго звена – 5 единицам, третьего звена – 2 единицам и четвертого звена – 4 единицам. Найдите общую длину ломаной.
Задача 2: Дана ломаная, состоящая из 5 звеньев. Известна длина каждого звена: первого – 2 единицы, второго – 4 единицы, третьего – 3 единицы, четвертого – 6 единиц и пятого – 1 единица. Найдите сумму длин всех звеньев.
Задача 3: Дана ломаная, состоящая из 6 звеньев. Известна длина первого звена – 4 единицы, а каждое следующее звено на 2 единицы длиннее предыдущего. Найдите длину последнего звена ломаной.
Задача 4: Дана ломаная, состоящая из 8 звеньев. Известно, что каждое звено данной ломаной на 1 единицу длиннее предыдущего звена. Найдите сумму длин всех звеньев ломаной.
Задача 5: Дана ломаная, состоящая из 9 звеньев. Длина первого звена равна 2 единицам. Каждое следующее звено на 3 единицы длиннее предыдущего. Найдите длину последнего звена ломаной.
Задача 6: Дана ломаная, состоящая из 10 звеньев. Известно, что каждое звено данной ломаной на 2 единицы короче предыдущего звена. Найдите сумму длин всех звеньев ломаной.
Задача 7: Дана ломаная, состоящая из 7 звеньев. Известна длина первого звена – 5 единиц, а каждое следующее звено короче предыдущего на 1 единицу. Найдите длину последнего звена ломаной.
Задача 8: Дана ломаная, состоящая из 6 звеньев. Длина последнего звена равна 12 единицам. Известно, что каждое звено данной ломаной на 2 единицы длиннее предыдущего звена. Найдите длину первого звена ломаной.
Задача 9: Дана ломаная, состоящая из 4 звеньев. Известна длина первого звена – 3 единицы, а каждое следующее звено на 1 единицу короче предыдущего. Найдите сумму длин всех звеньев ломаной.
Задача 10: Дана ломаная, состоящая из 8 звеньев. Известно, что каждое звено данной ломаной на 3 единицы длиннее предыдущего звена. Найдите сумму длин всех звеньев ломаной.






